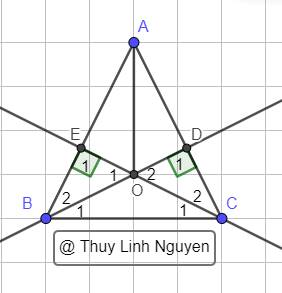
`a)`
Có `Delta ABC` cân tại `A(g t)`
`=>hat(ABC)=hat(ACB)`
`=>hat(EBC)=hat(DCB)`
Xét `Delta BEC` và `Delta CDB` có :
`{:(hat(E_1)=hat(D_1)(=90^0)),(BC-chung),(hat(EBC)=hat(DCB)(cmt)):}}`
`=>Delta BEC=Delta CDB(c.h-g.n)`
`=>CE=BD` ( 2 cạnh tương ứng )( dpcm )
`b)`
Có `Delta BEC=Delta CDB(cmt)`
`=>hat(C_1)=hat(B_1)` ( 2 góc tương ứng )
`=>Delta BOC` cân tại `O`
`=>OB=OC`(dpcm)
Xét `Delta OEB` và `Delta ODC` có :
`{:(hat(E_1)=hat(D_1)(=90^0)),(OB=OC(cmt)),(hat(O_1)=hat(O_2)(doi.di nh)):}}`
`=>Delta OEB=Delta ODC(c.h-g.n)`
`=>OE=OD`( 2 cạnh tương ứng )(dpcm)
`c)`
Có `Delta ABC` cân tại `A(g t)`
`=>AB=AC`
`=>A in ` trung trực của `Delta ABC(1)`
Có `OB=OC(cmt)`
`=>O in` trung trực của `Delta ABC(2)`
Từ `(1)` và `(2)=>OA` là trung trực `Delta ABC`
mà `Delta ABC` cân tại `A`
Nên `OA` là phân giác `hat(BAC)` (dpcm)