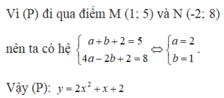Xác định parabol y=ax^2+bx+1 biết đi qua điểm N(1;4)có tung độ đỉnh là 0

Những câu hỏi liên quan
Xác định parabol y = ax2 + bx + 2, biết rằng parabol đó: Đi qua hai điểm M(1; 5) và N(-2; 8)
+ Parabol y = ax2 + bx + 2 đi qua M(1 ; 5)
⇒ 5 = a.12 + b.1 + 2 ⇒ a + b = 3 (1) .
+ Parabol y = ax2 + bx + 2 đi qua N(–2; 8)
⇒ 8 = a.( –2)2 + b.( –2) + 2 ⇒ 4a – 2b = 6 (2).
Từ (1) và (2) suy ra: a = 2; b = 1.
Vậy parabol cần tìm là y = 2x2 + x + 2.
Đúng 0
Bình luận (0)
Xác định Parabol (P): y a
x
2
+ bx + 2 biết rằng Parabol đi qua hai điểm M (1; 5) và N (2; −2). A. y −5
x
2
+ 8x + 2 B. y 10
x
2
+ 13x + 2 C. y −10
x
2
− 13x + 2 D. y 9
x
2
+ 6x – 5
Đọc tiếp
Xác định Parabol (P): y = a x 2 + bx + 2 biết rằng Parabol đi qua hai điểm M (1; 5) và N (2; −2).
A. y = −5 x 2 + 8x + 2
B. y = 10 x 2 + 13x + 2
C. y = −10 x 2 − 13x + 2
D. y = 9 x 2 + 6x – 5
Xác định parabol (P): y a
x
2
+ bx + 2, biết rằng (P) đi qua hai điểm M (1; 5) và N (−2; 8). A. y 2
x
2
+ x + 2. B. y
x
2
+ x + 2. C. y −2
x
2
+ x + 2. D. y −2
x
2
– x + 2.
Đọc tiếp
Xác định parabol (P): y = a x 2 + bx + 2, biết rằng (P) đi qua hai điểm M (1; 5) và N (−2; 8).
A. y = 2 x 2 + x + 2.
B. y = x 2 + x + 2.
C. y = −2 x 2 + x + 2.
D. y = −2 x 2 – x + 2.
xác định hàm số bậc 2 có đồ thị là parabol (p) biết : a, (P) : y= ax^2 + bx + c có giá trị nhỏ nhất = -1 biết (p) đi qua điểm A( -1 ; 7) và (P) cắt Oy tại điểm có tung độ bằng 1
Từ điều kiện đề bài: (hiển nhiên a khác 0):
\(\left\{{}\begin{matrix}\dfrac{4ac-b^2}{4a}=-1\\a-b+c=7\\c=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}4a-b^2=-4a\\a-b=6\\c=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(a-6\right)^2-8a=0\\b=a-6\\c=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\left\{2;18\right\}\\b=a-6\\c=1\end{matrix}\right.\)
Có 2 parabol thỏa mãn: \(\left[{}\begin{matrix}y=2x^2-4x+1\\y=18x^2+12x+1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Xác định Parabol (P) : y = ax^2 + bx + c ( a khác 0 ) biết (P) đi qua :
a, điểm E (0; 6) và hàm số y = ax^2 - bx + c đạt giá trị nhỏ nhất là 4 khi x = -2
b, điểm F (1; 16) và cắt Ox tại các điểm có hoành độ là -1 và 5.
Xác định parabol y = ax2 + bx + 2, biết rằng parabol đó: Đi qua điểm B(-1; 6) và tung độ của đỉnh là -1/4.
+ Parabol y = ax2 + bx + 2 đi qua điểm B(–1 ; 6)
⇒ 6 = a.( –1)2 + b.( –1) + 2 ⇒ a = b + 4 (1)
+ Parabol y = ax2 + bx + 2 có tung độ của đỉnh là –1/4
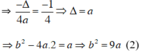
Thay (1) vào (2) ta được: b2 = 9.(b + 4) ⇔ b2 – 9b – 36 = 0.
Phương trình có hai nghiệm b = 12 hoặc b = –3.
Với b = 12 thì a = 16.
Với b = –3 thì a = 1.
Vậy có hai parabol thỏa mãn là y = 16x2 + 12b + 2 và y = x2 – 3x + 2.
Đúng 1
Bình luận (0)
Xác định số parabol y= ax^2+ x+c biết parabol đi qua điểm A ( 2;4) và có trục đối xứng x= 1/2
\(\Leftrightarrow\left\{{}\begin{matrix}4a+c=2\\-\dfrac{b}{2a}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=2-4a=2-4\cdot\left(-1\right)=6\\a=-1\end{matrix}\right.\)
Đúng 2
Bình luận (0)