Giải phương trình bằng phương pháp đặt ẩn phụ
\(x^2+5x+7=7\sqrt{x^3+1}\)
Những câu hỏi liên quan
giải phương trình bằng phương pháp đặt ẩn phụ:
ạ) \(2\sqrt{\left(-2x^2+5x+7\right)}=x^3-3x^2-x+12\)
b) \(x^2-3x+3=\left(4+3x-\frac{4}{x}\right)\sqrt{\left(x-1\right)}\)
Giải phương trình bằng cách đặt ẩn phụ: x - x = 5 x + 7
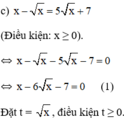
Khi đó (1) trở thành: t2 – 6t – 7 = 0 (2)
Giải (2): Có a = 1; b = -6; c = -7
⇒ a – b + c = 0
⇒ (2) có nghiệm t1 = -1; t2 = -c/a = 7.
Đối chiếu điều kiện chỉ có nghiệm t = 7 thỏa mãn.
+ Với t = 7 ⇒ √x = 7 ⇔ x = 49 (thỏa mãn).
Vậy phương trình đã cho có nghiệm x = 49.
Đúng 0
Bình luận (0)
gpt bằng phương pháp đặt ẩn phụ đưa về pt đẳng cấp:
\(\sqrt{5x^2-14x+9}-\sqrt{x^2-x+1}=2\left(x^2-4x+7\right)\sqrt{x-2}\)
Giải phương trình bằng phương pháp đặt ẩn phụ
\(x^2+5x+7=6\sqrt{x^3+7x}\)
15 tháng 3 2022 lúc 22:06
Giải phương trình (bằng phương pháp ẩn phụ): \(\sqrt{x-\sqrt{x^2-1}}+\sqrt{x+\sqrt{x^2-1}}=2\).
ĐKXĐ: \(x\ge1\)
Do \(\sqrt{x-\sqrt{x^2-1}}.\sqrt{x+\sqrt{x^2-1}}=\sqrt{x^2-x^2+1}=1\)
Đặt \(\sqrt{x-\sqrt{x^2-1}}=t\Rightarrow\sqrt{x+\sqrt{x^2-1}}=\dfrac{1}{t}\)
Phương trình trở thành:
\(t+\dfrac{1}{t}=2\Rightarrow t^2-2t+1=0\Rightarrow t=1\)
\(\Rightarrow\sqrt{x-\sqrt{x^2-1}}=1\Leftrightarrow x-\sqrt{x^2-1}=1\)
\(\Leftrightarrow x-1=\sqrt{x^2-1}\)
\(\Rightarrow x^2-2x+1=x^2-1\)
\(\Rightarrow x=1\) (thỏa mãn)
Đúng 0
Bình luận (0)
Giải phương trình \(\sqrt{3x+1}+\sqrt{2x-1}+x^2+2x-6=0\) bằng phương pháp đặt ẩn phụ
16 tháng 3 2022 lúc 19:08
Giải phương trình (bằng phương pháp ẩn phụ): \(\sqrt{x^2-x+1}+\sqrt{x^2-9x+9}=2x\)
\(\sqrt{x^2-x+1}+\sqrt{x^2-9x+9}=2x\)
=>\(\sqrt{x^2-x+1}-x+\sqrt{x^2-9x+9}-x=0\)
=>\(\dfrac{x^2-x+1-x^2}{\sqrt{x^2-x+1}+x}+\dfrac{x^2-9x+9-x^2}{\sqrt{x^2-9x+9}+x}=0\)
=>\(\left(-x+1\right)\left(\dfrac{1}{\sqrt{x^2-x+1}+x}+\dfrac{9}{\sqrt{x^2-9x+9}+x}\right)=0\)
=>-x+1=0
=>x=1
Đúng 0
Bình luận (0)
Giải các phương trình sau bằng phương pháp đặt ẩn phụ: 3 x 2 + x + 1 – x = x 2 + 3
giải phương trình : ( phương pháp đặt ẩn phụ nha bạn)
\(\frac{1}{1-x^2}=\frac{3}{\sqrt{1-x^2}}-1\)
Thích đặt ẩn phụ thì đặt vậy
Đặt \(\frac{1}{\sqrt{1-x^2}}=a\left(a>0\right)\) thì PT trở thành
\(a^2=3a-1\)
\(\Leftrightarrow\orbr{\begin{cases}a=\frac{3+\sqrt{5}}{2}\\a=\frac{3-\sqrt{5}}{2}\end{cases}}\)
Thế vô làm tiếp nhé
Đúng 0
Bình luận (0)
Xem thêm câu trả lời