cho hàm số f(x) xác định với mọi x thỏa mãn f(X) +2f(1/x) = X^2 tính f(2019)

Những câu hỏi liên quan
cho hàm số f(x) xác định với mọi x thỏa mãn f(X) +2f(1/x) = X^2 tính f(1/3)
hàm số f(x) xác định với mọi x thỏa mãn \(f\left(x\right)+2f\left(\frac{1}{x}\right)=x^2\)nên:
+) x = 3 thì \(f\left(3\right)+2f\left(\frac{1}{3}\right)=\frac{1}{9}\Rightarrow2f\left(3\right)+4f\left(\frac{1}{3}\right)=\frac{2}{9}\)(1)
+) x = \(\frac{1}{3}\)thì \(f\left(\frac{1}{3}\right)+2f\left(3\right)=9\)(2)
Lấy (1) - (2) ta được: \(3f\left(\frac{1}{3}\right)=\frac{-79}{9}\)
\(\Rightarrow f\left(\frac{1}{3}\right)=\frac{-79}{27}\)
Làm ngược, sửa:))
+) Nếu x = 3 thì \(f\left(3\right)+2f\left(\frac{1}{3}\right)=9\Rightarrow2f\left(3\right)+4f\left(\frac{1}{3}\right)=18\)(1)
+) Nếu x = \(\frac{1}{3}\) thì \(f\left(\frac{1}{3}\right)+2f\left(3\right)=\frac{1}{9}\)(2)
Lấy (1) - (2) ta được: \(3f\left(\frac{1}{3}\right)=\frac{161}{9}\)
\(\Rightarrow f\left(\frac{1}{3}\right)=\frac{161}{7}\)
1/cho hàm số f(x) thỏa mãn f(x) + 2f(2-x)=3x với mọi số thực x.Vậy f(2)=?
2/CHo hàm số f(x) xác định với mọi x thuộc R.Biết rằng với mọi x, ta đều có f(x)+3f(1/x)=x^2 Tính f(2), ta thu được kết quả là f(2)=
3/ TÍnh E=10,11+11,12+12,13+13,14+.........+ 98,99 + 99,10
1/cho hàm số f(x) thỏa mãn f(x) + 2f(2-x)=3x với mọi số thực x.Vậy f(2)=?
2/CHo hàm số f(x) xác định với mọi x thuộc R.Biết rằng với mọi x, ta đều có f(x)+3f(1/x)=x^2 Tính f(2), ta thu được kết quả là f(2)=
Mình vẫn chưa hiểu cái đề, mn giải thích cho mình nha
bài 1: f(x) + 2f(2-x)=3x (1)
f(2-x)+2[(2-(2-x)]=3(2-x) suy ra f(2-x)+2f(x)=6-3x suy ra 2f(2-x)+4f(x)=12-6x (2)
Lấy (2)-(1) ta có: 4f(x)-f(x)=12-6x-3x suy ra f(x)=4-3x
vậy f(2)=4-3*2=-2
Bài 2 tương tự: f(x)+3f(1/x)=x^2 (1)
f(1/x)+3f(x)=1/x^2 suy ra 3f(1/x)+9f(x)=3/x^2 (2)
Lấy (2)-(1) ta có: 9f(x)-f(x)=3/x^2-x^2 suy ra f(x)=(3-x^4)/8x^2
Vậy f(2)=(3-2^4)(8*2^2)=-13/32
Đúng 0
Bình luận (0)
Bài 2:
Đúng với x = 2 . => f(2) + 3f(1/2) = 2^2 = 4
=> f(2) + 3f(1/2) = 4 ( 1 )
Đúng với x = 1/2 => f(1/2) + 3f(2) = (1/2)^2 = 1/4.
=> 3f(2) + f (1/2) = 1/4.=> 9f(2) + 3f(1/2) = 3/4 ( 2 )
Lấy (2) trừ (1) ta đc : 8 f(2) = 3/4 - 4 = -13/4
=> f(2) = -13 / 32.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hàm số y = f(x) xác định với mọi x thuộc z (x >0) và thỏa mãn f(1)=1, f(a+b)= f(a) +f(b) - 2f(ab).
Tính f(2014) và f(2015)
Cho hàm số y = f(x) xác định với mọi x thuộc z (x >0) và thỏa mãn f(1)=1, f(a+b)= f(a) +f(b) - 2f(ab).
Tính f(2014) và f(2015)
Cho hàm số y = f(x) xác định với mọi x thuộc z (x >0) và thỏa mãn f(1)=1, f(a+b)= f(a) +f(b) - 2f(ab).
Tính f(2014) và f(2015)
cho hàm số f(x) được xác định với mọi x thuộc r,thỏa mãn tính chất f(x)-3f(x+1)=2x^2+1.a)tính f(2).b)xác định công thức hàm số f(x)
Cho hàm số y f(x) xác định trên R, thỏa mãn f(x)0 và f(x) + 2f(x) 0. Tính f(-1), biết rằng f(1) 1 A.
e
-
2
B.
e
3
C.
e
4
D. e
Đọc tiếp
Cho hàm số y = f(x) xác định trên R, thỏa mãn f(x)>0 và f'(x) + 2f(x) = 0. Tính f(-1), biết rằng f(1) = 1
A. e - 2
B. e 3
C. e 4
D. e
Cho hàm số yf(x) xác định trên R và có đạo hàm f‘(x) thỏa mãn f’(x)(1-x)(x+2).g(x) + 2018 trong đó g(x)0, mọi x thuộc R. Hàm số yf(1-x)+2018x+2019 nghịch biến trên khoảng nào?
Đọc tiếp
Cho hàm số y=f(x) xác định trên R và có đạo hàm f‘(x) thỏa mãn f’(x)=(1-x)(x+2).g(x) + 2018 trong đó g(x)<0, mọi x thuộc R. Hàm số y=f(1-x)+2018x+2019 nghịch biến trên khoảng nào?
![]()
![]()
![]()
![]()
Cho hàm số y f(x) xác định trên
ℝ
, thỏa mãn
f
x
0
,
∀
x
∈
ℝ
và f’(x) + 2f(x) 0. Tính f(-1), biết rằng f(1) 1. A.
e
-
2
B.
e
3
C.
e
4
D. 3
Đọc tiếp
Cho hàm số y = f(x) xác định trên ℝ , thỏa mãn f x > 0 , ∀ x ∈ ℝ và f’(x) + 2f(x) = 0. Tính f(-1), biết rằng f(1) = 1.
A. e - 2
B. e 3
C. e 4
D. 3
Chọn C.
Ta có f ' x + 2 f x = 0 ⇔ f ' x = - 2 f x ⇔ f ' x f x = - 2 d o f x > 0
Lấy tích phân hai vế, ta được
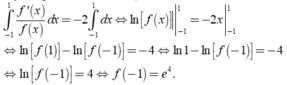
Đúng 0
Bình luận (0)