1. Cho 3 đường thẳng : y = x - 1 (d1) ; y = 2x - 3 (d2) ; y = kx +7 (d3)
Hãy tìm giá trị của k sao cho 3 đường thẳng đồng quy tại 1 điểm
2. Cho đường thẳng y = f(x) = (m + 4)x - m + 6
a) Tìm điểm cố định mà đường thẳng luôn đi qua mọi m
b) Xác định m để đường thẳng tạo với trục Ox một góc \(45^0\)















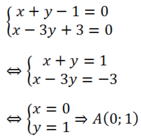
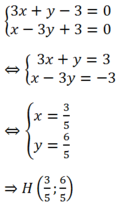
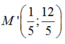
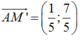
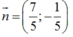
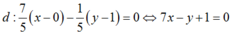






 help me pls
help me pls