đây nhé bạn

fraction{320}{3}

\(\dfrac{2bz-3cy}{a}=\dfrac{3cx-az}{2b}=\dfrac{ay-2bx}{3c}\\ \Rightarrow\dfrac{2abz-3acy}{a}=\dfrac{6bcx-2abz}{2b}=\dfrac{3acy-6bcx}{3c}\\ =\dfrac{\left(2abz-3acy\right)+\left(6bcx-2abz\right)+\left(3acy-6bcx\right)}{a+2b+3c}\\ =\dfrac{\left(2abz-2abz\right)+\left(3acy-3acy\right)+\left(6bcx-6bcx\right)}{a+2b+3c}=0\\ \)

\(\Rightarrow2bz-3cy=3cx-az=ay-2bx=0\\ \Rightarrow\left\{{}\begin{matrix}2bz=3cy\\3cx=az\\ay=2bx\end{matrix}\right.\)

\(2bz=3cy\Rightarrow\dfrac{2b}{y}=\dfrac{3c}{z}\\ 3cx=az\Rightarrow\dfrac{3c}{z}=\dfrac{a}{x}\\ ay=2bx\Rightarrow\dfrac{a}{x}=\dfrac{2b}{y}\\ \Rightarrow\dfrac{a}{x}=\dfrac{2b}{y}=\dfrac{3c}{z}\Rightarrow.....\)

Câu hỏi
# Cho dãy tỉ số bằng nhau ( 2bz-3cy )/a=(3cx az)/2b=(ay-2bx)/3c. Chứng minh: x/a=y/2b=z/3c.
Trả lời
Đáp án:+Giải thích các bước giải:


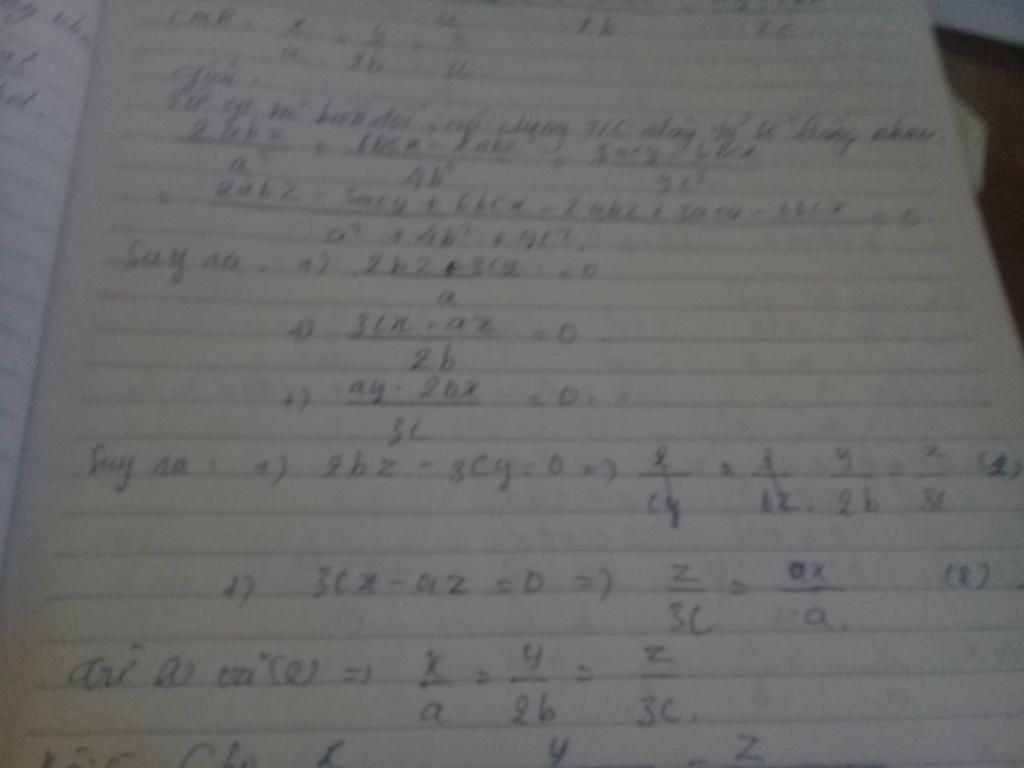
bạn tìm trên link này nhá mk ko gửi hình ảnh đc

Hoàng trung kiên , ngta đã làm gì đâu mà bạn chửi ?

bạn ơi. cho mk xin lỗi nhé bn

M<ình cho bạn phạm văn tuấn mượn nick mk  lên bạn ấy vào phá

Cho mk xin lỗi đc không

Mong bạn thứ lỗi cho mk nhé

Hôm nay mình mới được vào OLM thì mới thấy  caaub trả lời này bạn tuấn chửi tục bạn ạ

XIn lỗi mọi người nhiều

Ta có : \(\dfrac{2bz-3cy}{a}=\dfrac{3cx-az}{2b}=\dfrac{ay-2bx}{3c}\)

=> \(\dfrac{\left(2bz-3cy\right)a}{a^2}=\dfrac{\left(3cx-az\right)2b}{4b^2}=\dfrac{\left(ay-2bx\right)3c}{9c^2}\)

\(\dfrac{2bza-3cya}{a^2}=\dfrac{6cxb-2bza}{4b^2}=\dfrac{3cya-6cxb}{9c^2}\)

Áp dụng t/c dãy tỉ số bằng nhau :

\(\dfrac{2bza-3cya}{a^2}=\dfrac{6cxb-2bza}{4b^2}=\dfrac{3cya-6cxb}{9c^2}=\dfrac{2bza-3cya+6xb-2bza+3cya-6cxb}{a^2+4b^2+9c^2}=\dfrac{0}{a^2+4b^2+9c^2}=0\)Ta có : \(\dfrac{2bza-3cya}{a^2}=0\)

=> 2bza - 3cya = 0

=> 2bza = 3cya

=> \(\dfrac{y}{2b}=\dfrac{z}{3c}\) (1)

Ta có : \(\dfrac{6cxb-2bza}{4b^2}=0\)

=> 6cxb - 2bza = 0

=> 6cxb = 2bza

=> 3cx = za

=> \(\dfrac{z}{3c}=\dfrac{x}{a}\) (2)

Từ (1),(2) => \(\dfrac{x}{a}=\dfrac{y}{2b}=\dfrac{z}{3c}\) (ĐPCM)

Ta có: \(\frac{2bz-3cy}{a}=\frac{3cx-az}{2b}=\frac{ay-2bx}{3c}.\)

\(\Rightarrow\frac{a.\left(2bz-3cy\right)}{a^2}=\frac{2b.\left(3cx-az\right)}{4b^2}=\frac{3c.\left(ay-2bx\right)}{9c^2}.\)

\(\Rightarrow\frac{2abz-3acy}{a^2}=\frac{6bcx-2abz}{4b^2}=\frac{3acy-6bcx}{9c^2}.\)

Áp dụng tính chất dãy tỉ số bằng nhau ta được:

\(\frac{2abz-3acy}{a^2}=\frac{6bcx-2abz}{4b^2}=\frac{3acy-6bcx}{9c^2}=\frac{2abz-3acy+6bcx-2abz+3acy-6bcx}{a^2+4b^2+9c^2}=\frac{\left(2abz-2abz\right)-\left(3acy-3acy\right)+\left(6bcx-6bcx\right)}{a^2+4b^2+9c^2}=0.\)

\(\Rightarrow\left\{{}\begin{matrix}\frac{2bz-3cy}{a}=0\\\frac{3cx-az}{2b}=0\\\frac{ay-2bx}{3c}=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2bz-3cy=0\\3cx-az=0\\ay-2bx=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2bz=3cy\\3cx=az\\ay=2bx\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\frac{z}{3c}=\frac{y}{2b}\\\frac{x}{a}=\frac{z}{3c}\\\frac{y}{2b}=\frac{x}{a}\end{matrix}\right.\Rightarrow\frac{x}{a}=\frac{y}{2b}=\frac{z}{3c}\left(đpcm\right).\)

Chúc bạn học tốt!

https://goo.gl/xr4NMs

Là sao?

Từ\(\frac{2bz-3cy}{a}=\frac{3cx-az}{2b}\Rightarrow4b^2z-6bcy=3acx-a^2z\)

\(\Rightarrow\)\(\left(4b^2+a^2\right)z=3c\left(ax+2by\right)\)

\(\Rightarrow\frac{z}{3c}=\frac{ax+2by}{a^2+4b^2}=\frac{ax}{a^2}=\frac{2by}{4b^2}\Rightarrow\frac{z}{3c}=\frac{x}{a}=\frac{y}{2b}\)