Cho tam giác ABC trọng tâm G, I là trung điểm BC hãy xác định tổng của 2 vécto AI+GI

Những câu hỏi liên quan
Oxy cho tam giác ABC có trung điểm của BC là M(3;2). Trọng tâm và tâm đường tròn ngoại tiếp ABC lần lượt là \(G\left(\dfrac{2}{3};\dfrac{2}{3}\right)\)và\(I\left(1;-2\right)\). Xác định tọa độ đỉnh C
Cho hình chóp tam giác S.ABC, điểm G là trọng tâm của tam giác SBC. Gọi K là trung điểm của SA. hãy xác định giao điểm của đường thẳng KG và mặt phẳng (ABC)
Cho tam giác ABC biết I là trung điểm của đoạn thẳng AB, G là trọng tâm tam giác, M là điểm bất kỳ. Hãy chọn khẳng định đúng A.
M
A
→
+
M
B
→
+
M
C
→
2
M
G
→
B.
B...
Đọc tiếp
Cho tam giác ABC biết I là trung điểm của đoạn thẳng AB, G là trọng tâm tam giác, M là điểm bất kỳ. Hãy chọn khẳng định đúng
A. M A → + M B → + M C → = 2 M G →
B. B I → + I C → = 0 →
C. M A → + M B → = 3 M I →
D. M A → + M B → + M C → = 3 M G →
Cho tam giác ABC vẽ trọng tâm G của tam giác ,gọi M là trung điểm của cạnh BC ,trên tia đối của tia MG xác định điểm D sao cho MD=MG ,đoạn thẳng CG có phải là đường trung tuyến của tam giác ACD hay không ?
Cho tam giác ABC có A(–1; 1); B(5; –3); C(0; 2). Gọi G là trọng tâm của tam giác ABC. Hãy xác định tọa độ của điểm G1 là điểm đối xứng của G qua trục Oy.
A. G1 (4/3;0)
B. G1 (-4/3;3)
C. G1 (-4/3;2)
D. G1 (-4/3;0)
Do G là trọng tâm tam giác ABC nên tọa độ G:
x G = x A + x B + x C 3 = − 1 + 5 + 0 3 = 4 3 y G = y A + y B + y C 3 = 1 + ( − 3 ) + 2 3 = 0 ⇒ G 4 3 ; 0
Điểm G1 là điểm đối xứng của G qua trục Oy nên G 1 − 4 3 ; 0
Đáp án D
Đúng 0
Bình luận (0)
cho tam giác ABC. gọi M,N,E lần lượt là trung điểm BC,AC,AB.Trên tia đối của tia NE lấy điểm P sao cho N là trung điểm EP 1, CM: AECPEB 2, tam giác BEC tam giác PCE 3,CM: EN // BC,EN BC 4, Gọi G là trọng tâm của tam giác ABC. Trên tia SG lấy điểm D sao cho G là trung điểm AD. So sánh cạnh của tam giac BGD với các đường trung tuyến của tam giác ABC 5, So sánh các đương trung tuyến của tam giác BGD với các cạnh của tam giác abc 6, Từ E ke đường thẳng song song...
Đọc tiếp
cho tam giác ABC. gọi M,N,E lần lượt là trung điểm BC,AC,AB.Trên tia đối của tia NE lấy điểm P sao cho N là trung điểm EP
1, CM: AE=CP=EB
2, tam giác BEC= tam giác PCE
3,CM: EN // BC,EN= BC
4, Gọi G là trọng tâm của tam giác ABC. Trên tia SG lấy điểm D sao cho G là trung điểm AD. So sánh cạnh của tam giac BGD với các đường trung tuyến của tam giác ABC
5, So sánh các đương trung tuyến của tam giác BGD với các cạnh của tam giác abc
6, Từ E ke đường thẳng song song với BC cắt AM tại K.CM K là trung điểm của AM. CM G là trọng tâm của tam giác MNE
7, Đường thẳng ck cắt ab tại I. J là trung điểm của AJ và AI =\(\(\(\frac{1}{3}\)\)\)AB
8, CMR trong 3 dường trung tuyến của tam giác ABC tổng 2 đường còn lại
9, Trên tia AB lấy điểm B' sao cho B là trung điểm EB' .Trên tia HC lấy điểm C' sao cho C là trung điểm của AC. CM B',M,A" thẳng hàng
10, Cho AM =12cm, BN= 2cm, CF =15 cm. Tính BA
11, G là trọng tâm của tam giác ABC, coa cạnh BC cố định. CMR đường thẳng AG luôn đi qua 1 điểm cố định khi A thay đổi
12, Cho điểm O thay đổi trong tam giác ABC. Lấy O sao cho M' là trung điểm của OO'. Gọi M là trung điểm AO'. CM OM' luôn luôn đi qua 1 điểm cố định
Cho tam giác ABC
a) Dựng trọng tâm G của tam giác ấy
b) Gọi M là trung điểm của cạnh BC , trên tia đối của MG xác định điểm D sao cho MD=MG ; đoạn thẳng CG có phải là đường trung tuyến của tam giác ACD không ?
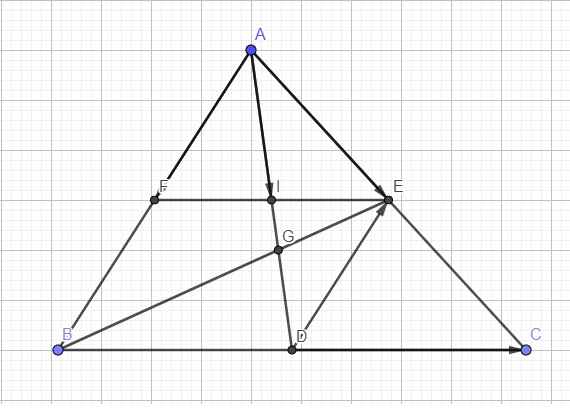
Cho tam giác ABC có trọng tâm G . các điểm D,E,F lần lượt là trung điểm của BC,CA,AB.và I là giao điểm của AD và EF . hãy phân tích các vecto AI,AG,DE,DC theo hai vecto AE ,AF
F là trung điểm AB \(\Rightarrow\overrightarrow{AF}=\dfrac{1}{2}\overrightarrow{AB}\) ; E là trung điểm AC \(\Rightarrow\overrightarrow{AE}=\dfrac{1}{2}\overrightarrow{AC}\)
Ta có EF song song BC (đường trung bình)
Mà D là trung điểm BC \(\Rightarrow\) I là trung điểm EF \(\Rightarrow AI\) là trung tuyến tam giác AEF
\(\Rightarrow\overrightarrow{AI}=\dfrac{1}{2}\overrightarrow{AE}+\dfrac{1}{2}\overrightarrow{AF}\)
Theo tính chất trọng tâm:
\(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AD}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{2}{3}\left(\overrightarrow{AE}+\overrightarrow{AF}\right)=\dfrac{2}{3}\overrightarrow{AE}+\dfrac{2}{3}\overrightarrow{AF}\)
DE là đường trung bình tam giác ABC
\(\Rightarrow\overrightarrow{DE}=\dfrac{1}{2}\overrightarrow{BA}=-\dfrac{1}{2}\overrightarrow{AB}=-\overrightarrow{AE}\) hay \(\overrightarrow{DE}=-\overrightarrow{AE}+0.\overrightarrow{AF}\)
D là trung điểm BC \(\Rightarrow\overrightarrow{DC}=\dfrac{1}{2}\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{DC}=\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{AC}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}=-\overrightarrow{AE}+\overrightarrow{AF}\)
Đúng 1
Bình luận (0)
Cho tam giác ABC nội tiếp (O;R), H là trực tâm của tam giác ABC, I là trung điểm của BC, AD là đường kính, CH giao AD tại E
a) chứng minh AB.AE=AH.AC
b) AI giao OH tại G, chứng minh G là trọng tâm của tam giác ABC