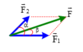
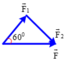
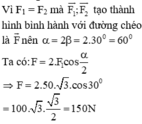Cho 2 lực F1 = 100N , F2 = 150N.Tính cường độ lực tổng hợp của 2 lực F1,F2 .
Những câu hỏi liên quan
cho 2 lực F1 , F2 có điểm đătj 0 là 60 độ . tì cường độ tổng 2 lực f1,f1 biết kooix lực = 60N
Phân tích lực
F
→
thành hai lực
F
1
→
v
à
F
2
→
, hai lực này vuông góc nhau. Biết độ lớn của lực F 100N,
F
1
60N thì độ lớn của lực
F
2
là: A. 80N B. 40N C. 160N D. 116,6N
Đọc tiếp
Phân tích lực F → thành hai lực F 1 → v à F 2 → , hai lực này vuông góc nhau. Biết độ lớn của lực F = 100N, F 1 = 60N thì độ lớn của lực F 2 là:
A. 80N
B. 40N
C. 160N
D. 116,6N
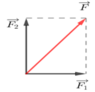
Ta có:
F 1 → ⊥ F 2 → ⇒ F 2 = F 1 2 + F 2 2 ⇒ F 2 = F 2 − F 1 2 = 100 2 − 60 2 = 80 N
Đáp án: A
Đúng 0
Bình luận (0)
Cho hai lực F1 và F2 có điểm đặt OVà vuông góc với nhau tìm Cường đó lực tổng hợp của hai lực ấy biết rằng cường độ lượng F1, F2 đều bằng 100 N
Theo bài ra ta có lực tổng hợp
F
→
F
1
→
+
F
2
→
và độ lớn của hai lực thành phần
F
1
F
2
50
3
(
N
)
và góc giữa lực tổng hợp
F...
Đọc tiếp
Theo bài ra ta có lực tổng hợp F → = F 1 → + F 2 → và độ lớn của hai lực thành phần F 1 = F 2 = 50 3 ( N ) và góc giữa lực tổng hợp F → v à F 1 → bằng β = 30 ° . Độ lớn của hợp lực F → và góc giữa F 1 → v à F 2 → bằng bao nhiêu?
A. 40 ° ; 40 N
B. 60 ° ; 150 N
C. 30 ° ; 10 N
D. 70 ° ; 0 N
Theo bài ra ta có lực tổng hợp
F
→
F
1
→
+
F
2
→
và độ lớn của hai lực thành phần
F
1
F
2
50
3
(
N...
Đọc tiếp
Theo bài ra ta có lực tổng hợp F → = F 1 → + F 2 → và độ lớn của hai lực thành phần F 1 = F 2 = 50 3 ( N ) và góc giữa lực tổng hợp F → và F 1 → bằng β = 30 0 . Độ lớn của hợp lực F → và góc giữa F 1 → với F 2 → bằng bao nhiêu?
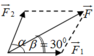
Vì F 1 = F 2 mà F 1 → ; F 2 → tạo thành hình bình hành với đường chéo là F → nên α = 2 β = 2.30 0 = 60 0
Ta có F = 2. F 1 cos α 2
⇒ F = 2.50. 3 . cos 30 0 = 100. 3 . 3 2 = 150 N
Đúng 0
Bình luận (0)
Cho hai lực F1 và F2 cùng có điểm đặt tại O. tìm cường độ lực của chúng trong trường hợp:? thứ nhất: vecto F1&F2 đều có cường độ là 100N,góc hợp bởi F1 và F2 bằng 120*. thứ hai:------------------------------------... dạng bài cộng hai vectơ đó.chỗ ------- là như trên,chắc mọi người hiểu.Cập nhật: hix chẳng biết yahoo hỏi đáp lỗi font gì mà lâu thế,em viết đủ rồi mà lúc gửi lại thiếu.trường hợp 2 thì mỗi lực F1 Và F2 lần lượt là 30N và 40N.góc tạo bởi hai lực là 90*.
Đọc tiếp
Cho hai lực F1 và F2 cùng có điểm đặt tại O. tìm cường độ lực của chúng trong trường hợp:?
thứ nhất: vecto F1&F2 đều có cường độ là 100N,góc hợp bởi F1 và F2 bằng 120*.thứ hai:------------------------------------...
dạng bài cộng hai vectơ đó.chỗ ------- là như trên,chắc mọi người hiểu.Cập nhật: hix chẳng biết yahoo hỏi đáp lỗi font gì mà lâu thế,em viết đủ rồi mà lúc gửi lại thiếu.trường hợp 2 thì mỗi lực F1 Và F2 lần lượt là 30N và 40N.góc tạo bởi hai lực là 90*.
a) gọi A và B là hai điểm cuối của vtF1 và vtF2
dựng hình bình hành OACB, qui tắc hình bình hành ta có:
vtF = vtF1 + vtF2 = vtOA + vtOB = vtOC
về độ lớn ta thấy:
gócOAC = 180o - 120o = 60o (2 góc kề bù của hbh)
OA = AC = 100N
=> tgiác OAC cân, có 1 góc 60o nên là tgiác đều
=> F = OC = OA = F1 = 100N
b) vẫn dựng hình bình hành OACB như trên
do giả thiết OA_|_OB nên OACB là hình chữ nhật
có OC = √(OA²+AC²) = √(30²+40²) = 50
vtF = vtF1 + vtF2 = vtOA + vtOB = vtOC
độ lớn: F = OC = 50N
Đúng 0
Bình luận (0)
Cho ba lực cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của hai lực F1, F2 đều là 100N và ∠AMB 60o. Tìm cường độ và hướng của lực F3.
Đọc tiếp
Cho ba lực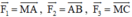 
cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của hai lực F1, F2 đều là 100N và ∠AMB = 60o. Tìm cường độ và hướng của lực F3.
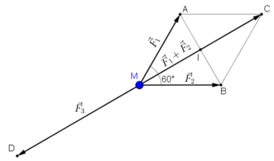
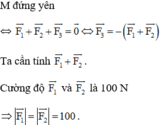
Ta biểu diễn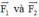 
bằng hai vec tơ 
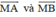như hình vẽ.
Khi đó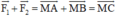 
(C là đỉnh còn lại của hình bình hành MACB).
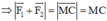
+ Tính MC : Gọi I là trung điểm của AB ⇒ I là trung điểm của MC.
Δ MAB có MA = MB = 100 và góc AMB = 60º nên là tam giác đều
⇒ đường cao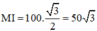 
⇒ MC = 2.MI = 100√3.
Vec tơ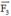 
là vec tơ đối của 
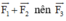có hướng ngược với 
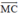và có cường độ bằng 100√3N.
Đúng 1
Bình luận (0)
Cho hai lực F1 và F2 có độ lớn F1=F2=6N. Vẽ hợp lực và tìm độ lớn của hợp lực khi
1. F1 cùng chiều F2
2. Góc ( F1,F2 ) = 120°
1/ Khi \(\overrightarrow{F_1}\uparrow\uparrow\overrightarrow{F_2}\Rightarrow\cos\left(\widehat{F_1;F_2}\right)=\cos0=0\)
\(\Rightarrow F^2=F_1^2+F_2^2\Leftrightarrow F=\sqrt{6^2+6^2}=6\sqrt{2}\left(N\right)\)
2/ \(F^2=F_1^2+F_2^2+2.F_1.F_2.\cos\left(\widehat{F_1;F_2}\right)\)
\(F=\sqrt{6^2+6^2+2.6.6.\cos120}=6\left(N\right)\)
Đúng 0
Bình luận (0)
Hợp lực của 2 lực
F
1
→
(
F
1
10
N
)
và
F
2
→
là lực
F
→
(
F
20
N
)
và
F
→
hợp với
F
1
→
một gó...
Đọc tiếp
Hợp lực của 2 lực F 1 → ( F 1 = 10 N ) và F 2 → là lực F → ( F = 20 N ) và F → hợp với F 1 → một góc 60 ° . Độ lớn của lực F 2 là?
A. 50 N
B. 10 2 N
C. 10 3 N
D. 20 2 N
