Cho hình thang ABCD (AB//CD) CD=2AB M là trung điểm AB
Đặt vt BM =vt a;vt BC =vt b.Trên đoạn MC lấy I sao cho MI=k .MC (k thuộc R) phân tích vt BI,BD theo vt a và b .tìm k để B,I,D thẳng hàng
Cho hình thang ABCD (AB // CD), M là trung điểm của CD. Gọi H là giao điểm của AM và BD, K là giao điểm của BM và AC.
a) C/m AH/HM = 2AB/CD
b) Chứng minh IK // AB.
c) Đặt AB = a, CD= b. Tính HK theo a và b
a. -Xét △ABH có: AB//DM (gt)
\(\Rightarrow\dfrac{AH}{HM}=\dfrac{AB}{DM}\) (định lí Ta-let)
Mà \(DM=\dfrac{1}{2}CD\) (M là trung điểm CD).
\(\Rightarrow\dfrac{AH}{HM}=\dfrac{AB}{\dfrac{1}{2}CD}=\dfrac{2AB}{CD}\)
b. Sửa đề: C/m HK//AB.
-Xét △ABK có: AB//CM (gt)
\(\Rightarrow\dfrac{AK}{KC}=\dfrac{AB}{CM}\) (định lí Ta-let)
Mà \(CM=\dfrac{1}{2}CD\) (M là trung điểm CD).
\(\Rightarrow\dfrac{AK}{KC}=\dfrac{AB}{\dfrac{1}{2}CD}=\dfrac{2AB}{CD}\)
-Xét △ABM có: \(\dfrac{AH}{HM}=\dfrac{AK}{KC}\left(=\dfrac{2AB}{CD}\right)\)
\(\Rightarrow\)HK//AB.
c. -Xét △ABM có: HK//AB (cmt).
\(\Rightarrow\dfrac{AB}{HK}=\dfrac{AM}{HM}\) (định lí Ta-let).
\(\Rightarrow\dfrac{AB-HK}{HK}=\dfrac{AM-HM}{HM}\)
\(\Rightarrow\dfrac{AB}{HK}-1=\dfrac{AH}{HM}\)
Mà \(\dfrac{AH}{HM}=\dfrac{2AB}{CD}\left(cmt\right)\)
\(\Rightarrow\dfrac{AB}{HK}=\dfrac{2AB}{CD}\)
\(\Rightarrow\dfrac{a}{HK}=\dfrac{2a}{b}\)
\(\Rightarrow HK=\dfrac{b}{a}\)
Cho hình thang ABCD (AB//CD) có CD = 2AB. Gọi M là trung điểm của CĐ. C/m: a) AM // BC b) AD = BM. Giải giúp em với ạ 🥲
a: Xét tứ giác ABCM có
AB//CM
AB=CM
Do đó: ABCM là hình bình hàn
Suy ra: AM//BC
cho tứ giác ABCD .lấy điểm M và N lần lượt là trung điểm của AB và CD . I là trung điểm của MN . chứng minh rằng vt IA+ vt IB+ vt IC+ vt ID =0
dễ mà ,mình bỏ chữ vecto nha
IA+IB+IC+ID=IM+MA+IM+MB+IN+NC+IN+ND
=2IM+2IN+MA+MB+NC+ND
=0
Cho hình thang vuông ABCD vuông tại A,D với AB=AD=a, CD=2a gọi O là giao điểm của AC và BD. Tím độ dài các vt OC, vt OB
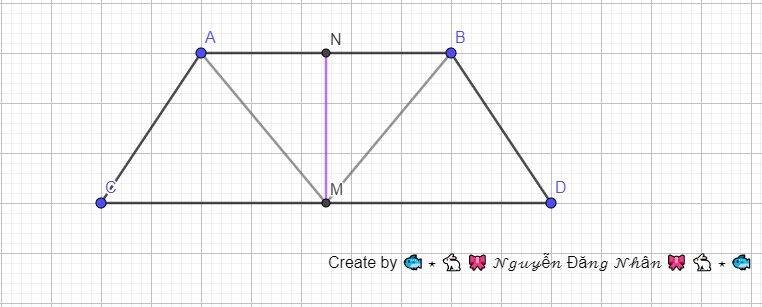
Cho hình thang cân ABCD có AB song song với CD. Lấy M, N lần lượt là trung điểm CD, AB.
a) cm AM=BM
b) cm MN là đường cao của hình thang
a) Xét 2 tam giác AMC và BMD có:
\(\widehat{C}=\widehat{D}\) (góc kề một đáy)
\(AC=BD\) (cạnh bên)
\(MC=MD\) (giả thiết)
\(\Rightarrow\Delta AMC=\Delta BMC\) (cạnh.góc.cạnh)
\(\Rightarrow AM=BM\)
b) Xét 2 tam giác NMA và NMB có:
\(NA=NB\) (giả thiết)
\(NM\): cạnh chung
\(MA=MB\) (chứng minh trên)
\(\Rightarrow\Delta NMA=\Delta NMB\)
\(\Rightarrow\widehat{MNA}=\widehat{MNB}\)
Mà 2 góc \(\widehat{MNA}=\widehat{MNB}\) là 2 góc kề bù, nên:
\(\widehat{MNA}=\widehat{MNB}=\dfrac{180^o}{2}=90^o\)
Vậy MN là đường cao:
1) cho hình thang ABCD có AB//CD;AB>CD;AC vuông góc với BD.Trên cạnh đáy AB lấy điểm M sao cho AM bằng độ dài đường trung bình của hình thang ABCD .CM:AC là tia phân giác góc A
2)Cho hình thang ABCD có góc A=góc B=90 độ ;BC=2AD=2AB .Gọi M là 1 điểm trên đáy nhỏ AB kẻ Mx vuông với MB .Mx cắt CD tại N.CM:MB=MN
cho hình thang ABCD[AB//CD],M là trung điểm của CD . Gọi E là giao điểm của AC và BM ,F là giao điểm của BD và AM .Đường thẳng EF cắt BC và AD lần lượt tại G và H.
a>CMinh:EA/EC=2AB/CD
b>CMinh:EF//CD
c>CMinh:GE=EF=FH
a: Xét ΔEAB và ΔECM có
\(\widehat{EAB}=\widehat{ECM}\)(hai góc so le trong, AB//CM)
\(\widehat{AEB}=\widehat{CEM}\)(hai góc đối đỉnh)
Do đó: ΔEAB đồng dạng với ΔECM
=>\(\dfrac{EA}{EC}=\dfrac{EB}{EM}=\dfrac{AB}{CM}\)
=>\(\dfrac{EA}{EC}=\dfrac{AB}{CM}=AB:\dfrac{CD}{2}=2\cdot\dfrac{BA}{CD}\)
b: Xét ΔFAB và ΔFMD có
\(\widehat{FAB}=\widehat{FMD}\)(hai góc so le trong, AB//DM)
\(\widehat{AFB}=\widehat{MFD}\)(hai góc đối đỉnh)
Do đó: ΔFAB đồng dạng với ΔFMD
=>\(\dfrac{FA}{FM}=\dfrac{FB}{FD}=\dfrac{AB}{MD}\)
Ta có: \(\dfrac{FA}{FM}=\dfrac{AB}{MD}\)
\(\dfrac{EB}{EM}=\dfrac{AB}{CM}\)
mà MD=MC
nên \(\dfrac{FA}{FM}=\dfrac{EB}{EM}\)
=>\(\dfrac{MF}{FA}=\dfrac{ME}{EB}\)
Xét ΔMAB có \(\dfrac{MF}{FA}=\dfrac{ME}{EB}\)
nên FE//AB
Ta có: FE//AB
AB//CD
Do đó: FE//CD
c: Xét ΔADM có HF//DM
nên \(\dfrac{HF}{DM}=\dfrac{AF}{AM}\)
Xét ΔBDM có FE//DM
nên \(\dfrac{FE}{DM}=\dfrac{BE}{BM}\)
Xét ΔBMC có EG//MC
nên \(\dfrac{EG}{MC}=\dfrac{BE}{BM}\)
mà \(\dfrac{FE}{DM}=\dfrac{BE}{BM}\)
và MC=MD
nên FE=EG
Ta có: \(\dfrac{AF}{FM}=\dfrac{BE}{EM}\)
=>\(\dfrac{FM}{FA}=\dfrac{EM}{BE}\)
=>\(\dfrac{FM}{FA}+1=\dfrac{EM}{BE}+1\)
=>\(\dfrac{FM+FA}{FA}=\dfrac{EM+BE}{BE}\)
=>\(\dfrac{AM}{FA}=\dfrac{BM}{BE}\)
=>\(\dfrac{AF}{AM}=\dfrac{BE}{BM}\)
mà \(\dfrac{HF}{DM}=\dfrac{AF}{AM}\) và \(\dfrac{BE}{BM}=\dfrac{FE}{DM}\)
nên HF=FE
mà FE=EG
nên HF=FE=EG
1) Cho hình thang ABCD ( AB//AB) và AC=CD. Tính các góc hình thang cân
2) Cho hình thang ABCD có góc A = 90 0 và BC = 2AD = 2AB Gọi M là 1 điểm trên đáy nhỏ AD , Kẻ Mx vuông góc BM và Mx cắt CD tại N
. C/m MB=MN