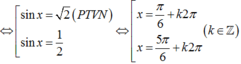Giai phương trình : \(sin^2x-4sinx+3=0\)
Những câu hỏi liên quan
\(2\sin\left(2x-\frac{\pi}{6}\right)+4sinx=0\)
Nghiệm của phương trình sin2x - 4sinx + 3 0 là :
Đọc tiếp
Nghiệm của phương trình sin2x - 4sinx + 3 = 0 là :
Giải phương trình 3tan2x + 4sin2x - 2
3
tanx - 4sinx + 2 0 A. x ±
π
6
+ k2π, k ∈ Z B. x
π
6
+ kπ, k ∈ Z C. x
-
π
4
+ k2π,
-
π
6
+ k2π, k ∈ Z D. Tất cả sai
Đọc tiếp
Giải phương trình 3tan2x + 4sin2x - 2 3 tanx - 4sinx + 2 = 0
A. x = ± π 6 + k2π, k ∈ Z
B. x = π 6 + kπ, k ∈ Z
C. x = - π 4 + k2π, - π 6 + k2π, k ∈ Z
D. Tất cả sai
Giải pt:
\(sin^3x-cos^3x+3sin^2x+4sinx-cosx+2=0\)
\(\Leftrightarrow sin^3x+3sin^2x+3sinx+1-cos^3x+sinx-cosx+1=0\)
\(\Leftrightarrow\left(sinx+1\right)^3-cos^3x+sinx-cosx+1=0\)
\(\Leftrightarrow\left(sinx-cosx+1\right)\left[\left(sinx+1\right)^2+cosx\left(sinx+1\right)+cos^2x\right]+sinx-cosx+1=0\)
\(\Leftrightarrow\left(sinx-cosx+1\right)\left(2sinx+sinx.cosx+cosx+2\right)+sinx-cosx+1=0\)
\(\Leftrightarrow\left(sinx-cosx+1\right)\left(2sinx+cosx+sinx.cosx+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx-cosx=-1\Leftrightarrow sin\left(x-\frac{\pi}{4}\right)=-\frac{\sqrt{2}}{2}\Leftrightarrow...\\2sinx+cosx+sinx.cosx+3=0\left(1\right)\end{matrix}\right.\)
Xét (1):
\(\Leftrightarrow2\left(sinx+1\right)+cosx\left(sinx+1\right)+1=0\)
\(\Leftrightarrow\left(cosx+2\right)\left(sinx+1\right)+1=0\)
Do \(sinx;cosx\ge-1\Rightarrow\left(cosx+2\right)\left(sinx+1\right)\ge0\)
\(\Rightarrow\left(cosx+2\right)\left(sinx+1\right)+1=0\) vô nghiệm
Phương trình sinum
Giải các phương trình sau:
1. sinx.cosx 0
2. cosx + sinx -1
3. sinx.cosx.cos2x 0
4. sin2x - 4sinx + 3 0
5. sin2x + cos2x 1
6. 2sin2x + 1 0
7. sin (2x - 400) frac{sqrt{3}}{2} với -1800 le x le 1800
8. 2sinx + sqrt{2} 0
Đọc tiếp
Phương trình sinu=m
Giải các phương trình sau:
1. sinx.cosx = 0
2. cosx + sinx = -1
3. sinx.cosx.cos2x = 0
4. sin2x - 4sinx + 3 = 0
5. sin2x + cos2x = 1
6. 2sin2x + 1= 0
7. sin (2x - 400) =\(\frac{\sqrt{3}}{2}\) với -1800 \(\le\) x \(\le\) 1800
8. 2sinx + \(\sqrt{2}\) =0
1.
\(\Leftrightarrow2sinx.cosx=0\)
\(\Leftrightarrow sin2x=0\)
\(\Leftrightarrow2x=k\pi\)
\(\Leftrightarrow x=\frac{k\pi}{2}\)
2.
\(\Leftrightarrow\frac{\sqrt{2}}{2}sinx+\frac{\sqrt{2}}{2}cosx=-\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(x+\frac{\pi}{4}\right)=-\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\frac{\pi}{4}=-\frac{\pi}{4}+k2\pi\\x+\frac{\pi}{4}=\frac{5\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{2}+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
3.
\(\Leftrightarrow2.\left(2sinx.cosx\right)cos2x=0\)
\(\Leftrightarrow2sin2x.cos2x=0\)
\(\Leftrightarrow sin4x=0\)
\(\Leftrightarrow4x=k\pi\)
\(\Leftrightarrow x=\frac{k\pi}{4}\)
4.
\(\Leftrightarrow\left(sinx-1\right)\left(sinx-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=1\\sinx=3>1\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow x=\frac{\pi}{2}+k2\pi\)
Đúng 0
Bình luận (0)
5.
\(\Leftrightarrow\frac{\sqrt{2}}{2}sin2x+\frac{\sqrt{2}}{2}cos2x=\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin2x.sin\frac{\pi}{4}+cos2x.cos\frac{\pi}{4}=\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(2x+\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+\frac{\pi}{4}=\frac{\pi}{4}+k2\pi\\2x+\frac{\pi}{4}=\frac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\frac{\pi}{4}+k\pi\end{matrix}\right.\)
6.
\(\Leftrightarrow2sin2x=-1\)
\(\Leftrightarrow sin2x=-\frac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=-\frac{\pi}{6}+k2\pi\\2x=\frac{7\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{12}+k\pi\\x=\frac{7\pi}{12}+k\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Trên đoạn [ - π ; π ] phương trình 4sinx-3 = 0 có tất cả bao nhiêu nghiệm?
A. 1
B. 0
C. 2
D. 4
Trên đoạn - π ; π phương trình 4 sin x - 3 = 0 có tất cả bao nhiêu nghiệm?
A. 1
B. 0
C. 2
D. 4
Đáp án C
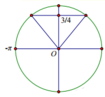
Phương trình đã cho ⇔ sin x = 3 4 ( 1 ) Quan sát đường tròn
lượng giác ta thấy có 2 giá trị của x ∈ - π ; π thỏa mãn phương trình (1).
Đúng 0
Bình luận (0)
Tìm góc
α
∈
π
6
;
π
4
;
π
3
;
π
2
để phương trình
cos
2
x
+
3
sin
2
x...
Đọc tiếp
Tìm góc α ∈ π 6 ; π 4 ; π 3 ; π 2 để phương trình cos 2 x + 3 sin 2 x - 2 cos x = 0 tương đương với phương trình cos ( 2 x - α ) = cos x
Đáp án D
Ta có
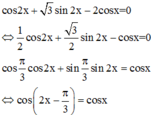
Do đó để phương trình 
tương đương với phương trình
Đúng 0
Bình luận (0)
Phương trình:
cos
(
2
x
+
π
4
)
+
cos
(
2
x
-
π
4
)
+
4
sin
x
2
+
2
(
1
-
sin
x
)
có nghiệm là:
Đọc tiếp
Phương trình: cos ( 2 x + π 4 ) + cos ( 2 x - π 4 ) + 4 sin x = 2 + 2 ( 1 - sin x ) có nghiệm là:
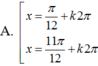
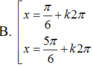
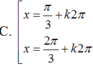
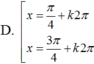
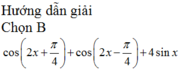
1 2 ( cos 2 x - sin 2 x ) + 1 2 ( cos 2 x + sin 2 x ) + 4 sin x = 2 + 2 ( 1 - sin x )
Đúng 0
Bình luận (0)