Tìm a để hàm số xác định trên nửa khoảng (-2;5]. Hàm số: \(\frac{4x^2+1}{(\sqrt{2a+7-x})(x-5-a^2)}-\sqrt{x+8-a}\)

Những câu hỏi liên quan
Cho hàm số yf(x) xác định và liên tục trên mỗi nửa khoảng (-∞;-2] và [2;+∞), có bảng biến thiên như hình trênTìm tập hợp các giá trị của m để phương trình f(x)m có hai nghiệm phân biệt A. (-7/4;2]
∪
[22;
+
∞
) B. (7/4;2] C. [22;
+
∞
) D. (7/4;2]
∪
[22;
+
∞
)
Đọc tiếp
Cho hàm số y=f(x) xác định và liên tục trên mỗi nửa khoảng (-∞;-2] và [2;+∞), có bảng biến thiên như hình trên
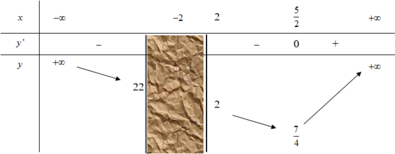
Tìm tập hợp các giá trị của m để phương trình f(x)=m có hai nghiệm phân biệt
A. (-7/4;2] ∪ [22; + ∞ )
B. (7/4;2]
C. [22; + ∞ )
D. (7/4;2] ∪ [22; + ∞ )
Cho hàm số
y
f
x
xác định và liên tục trên mỗi nửa khoảng
(
-
∞
;
-
2
]
và
[
2
;
+
∞
)
, có bảng biến th...
Đọc tiếp
Cho hàm số y = f x xác định và liên tục trên mỗi nửa khoảng ( - ∞ ; - 2 ] và [ 2 ; + ∞ ) , có bảng biến thiên như hình vẽ dưới
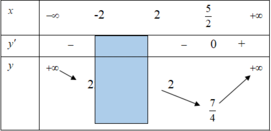
Tìm tập hợp các giá trị của m để phương trình f x = m có hai nghiệm phân biệt
A. 7 4 ; 2 ∪ 22 ; + ∞
B. [ 22 ; + ∞ )
C. 7 4 ; + ∞
D. ( 7 4 ; 2 ] ∪ 22 ; + ∞
Chọn đáp án D
Xét trên mỗi nửa khoảng ( - ∞ ; - 2 ] v à [ 2 ; + ∞ )
Để phương trình f x = m có hai nghiệm phân biệt
⇔ Đồ thị hàm số y = f x cắt đường thẳng y = m tại hai điểm phân biệt. Từ bảng biến thiên suy ra
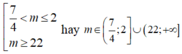
Đúng 0
Bình luận (0)
Tìm m để hàm số
y
-
m
x
+
2
2
x
-
m
luôn nghịch biến trên khoảng xác định. A.-2 m ≤ 2 B. m -2 hoặc m 2 C. -2 m 2 D. m ≠ ±2
Đọc tiếp
Tìm m để hàm số y = - m x + 2 2 x - m luôn nghịch biến trên khoảng xác định.
A.-2 < m ≤ 2
B. m < -2 hoặc m > 2
C. -2 < m < 2
D. m ≠ ±2
Tập xác định
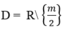
Hàm số nghịch biến trên từng khoảng
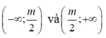
khi và chỉ khi
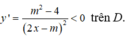
Suy ra m 2 - 4 < 0 hay -2 < m < 2. Chọn đáp án C.
Đúng 0
Bình luận (0)
Tìm m để hàm số f x = x x - m xác định trên khoảng (0;5).
A. 0 < m < 5
B. m ≤ 0
C. m ≥ 5
D. m ≤ 0 hoặc m ≥ 5
Hàm số f x = x x - m xác định khi x ≠ m .
Do đó, để hàm số đã cho xác định trên khoảng (0 ; 5) thì m ∉ 0 ; 5 . Do đó m ≤ 0 hoặc m ≥ 5 .
Đúng 0
Bình luận (0)
Cho hàm số:Khẳng định nào sau đây là đúng?A. Hàm số đồng biến trên từng khoảng xác định;B. Hàm số đồng biến trên khoảng (-
∞
;+
∞
);C. Hàm số nghịch biến trên từng khoảng xác định;D. Hàm số nghịch biến trên khoảng (-
∞
;+
∞
).
Đọc tiếp
Cho hàm số:
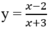
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên từng khoảng xác định;
B. Hàm số đồng biến trên khoảng (- ∞ ;+ ∞ );
C. Hàm số nghịch biến trên từng khoảng xác định;
D. Hàm số nghịch biến trên khoảng (- ∞ ;+ ∞ ).
tìm các giá trị của m để hàm số
a) \(y=\dfrac{x+m}{x+1}\) nghịch biến trên từng khoảng xác định
b) \(y=\dfrac{2x-3m}{x-m}\) đồng biến trên từng khoảng xác định
a: TXĐ: D=R\{-1}
\(y'=\dfrac{\left(x+m\right)'\left(x+1\right)-\left(x+1\right)'\left(x+m\right)}{\left(x+1\right)^2}\)
\(=\dfrac{x+1-x-m}{\left(x+1\right)^2}=\dfrac{1-m}{\left(x+1\right)^2}\)
Để hàm số nghịch biến trên từng khoảng xác định thì \(y'< 0\forall x\)
=>\(\dfrac{1-m}{\left(x+1\right)^2}< 0\)
=>1-m<0
=>m>1
b: TXĐ: D=R\{m}
\(y=\dfrac{2x-3m}{x-m}\)
=>\(y'=\dfrac{\left(2x-3m\right)'\left(x-m\right)-\left(2x-3m\right)\left(x-m\right)'}{\left(x-m\right)^2}\)
\(=\dfrac{2\left(x-m\right)-\left(2x-3m\right)}{\left(x-m\right)^2}=\dfrac{2x-2m-2x+3m}{\left(x-m\right)^2}\)
\(=\dfrac{m}{\left(x-m\right)^2}\)
Để hàm số đồng biến trên từng khoảng xác định thì \(y'>0\forall x\)
=>\(\dfrac{m}{\left(x-m\right)^2}>0\)
=>m>0
Đúng 0
Bình luận (0)
tìm các giá trị của m để hàm số
a) \(y=\dfrac{2m-x}{x-3}\) đồng biến trên từng khoảng xác định
b) \(y=\dfrac{x+3}{x+m}\) nghịch biến trên từng khoảng xác định
a: TXĐ: D=R\{3}
\(y=\dfrac{2m-x}{x-3}\)
=>\(y'=\dfrac{\left(2m-x\right)'\left(x-3\right)-\left(2m-x\right)\left(x-3\right)'}{\left(x-3\right)^2}\)
\(=\dfrac{-\left(x-3\right)-2m+x}{\left(x-3\right)^2}\)
\(=\dfrac{3-2m}{\left(x-3\right)^2}\)
Để hàm số đồng biến trên từng khoảng xác định thì y'>0 với mọi x thỏa mãn ĐKXĐ
=>\(\dfrac{3-2m}{\left(x-3\right)^2}>0\)
=>3-2m>0
=>2m<3
=>\(m< \dfrac{3}{2}\)
b: TXĐ: D=R\{-m}
\(y=\dfrac{x+3}{x+m}\)
=>\(y'=\dfrac{\left(x+3\right)'\left(x+m\right)-\left(x+3\right)\left(x+m\right)'}{\left(x+m\right)^2}\)
\(=\dfrac{x+m-x-3}{\left(x+m\right)^2}=\dfrac{m-3}{\left(x+m\right)^2}\)
Để hàm số nghịch biến trên từng khoảng xác định thì \(y'< 0\forall x\in TXĐ\)
=>\(\dfrac{m-3}{\left(x+m\right)^2}< 0\)
=>m-3<0
=>m<3
Đúng 0
Bình luận (0)
tìm các giá trị của m để hàm số
a) \(y=\dfrac{mx-2m-3}{x-m}\) đồng biến trên từng khoảng xác định
b) \(y=\dfrac{mx-4}{x-m}\) đồng biến trên từng khoảng xác định
a: ĐKXĐ: x<>m
=>TXĐ: D=R\{m}
\(y=\dfrac{mx-2m-3}{x-m}\)
=>\(y'=\dfrac{\left(mx-2m-3\right)'\cdot\left(x-m\right)-\left(mx-2m-3\right)\left(x-m\right)'}{\left(x-m\right)^2}\)
\(=\dfrac{m\left(x-m\right)-\left(mx-2m-3\right)}{\left(x-m\right)^2}\)
\(=\dfrac{mx-m^2-mx+2m+3}{\left(x-m\right)^2}=\dfrac{-m^2+2m+3}{\left(x-m\right)^2}\)
Để hàm số đồng biến trên từng khoảng xác định thì \(y'>0\forall x\in TXĐ\)
=>\(\dfrac{-m^2+2m+3}{\left(x-m\right)^2}>0\)
=>\(-m^2+2m+3>0\)
=>\(m^2-2m-3< 0\)
=>(m-3)(m+1)<0
TH1: \(\left\{{}\begin{matrix}m-3>0\\m+1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>3\\m< -1\end{matrix}\right.\)
=>\(m\in\varnothing\)
TH2: \(\left\{{}\begin{matrix}m-3< 0\\m+1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>-1\\m< 3\end{matrix}\right.\)
=>-1<m<3
b: TXĐ: D=R\{m}
\(y=\dfrac{mx-4}{x-m}\)
=>\(y'=\dfrac{\left(mx-4\right)'\left(x-m\right)-\left(mx-4\right)\left(x-m\right)'}{\left(x-m\right)^2}\)
\(=\dfrac{m\left(x-m\right)-\left(mx-4\right)}{\left(x-m\right)^2}\)
\(=\dfrac{mx-m^2-mx+4}{\left(x-m\right)^2}=\dfrac{-m^2+4}{\left(x-m\right)^2}\)
Để hàm số đồng biến trên từng khoảng xác định thì \(\dfrac{-m^2+4}{\left(x-m\right)^2}>0\)
=>\(-m^2+4>0\)
=>\(-m^2>-4\)
=>\(m^2< 4\)
=>-2<m<2
Đúng 0
Bình luận (0)
tìm các giá trị của m để hàm số
a) \(y=\dfrac{mx-2m+15}{x+m}\) đồng biến trên từng khoảng xác định
b) \(y=\dfrac{mx+4m}{x+m}\) đồng biến trên từng khoảng xác định
a: ĐKXĐ: x<>-m
=>TXĐ: D=R\{-m}
\(y=\dfrac{mx-2m+15}{x+m}\)
=>\(y'=\dfrac{\left(mx-2m+15\right)'\left(x+m\right)-\left(mx-2m+15\right)\left(x+m\right)'}{\left(x+m\right)^2}\)
\(=\dfrac{m\left(x+m\right)-mx+2m-15}{\left(x+m\right)^2}\)
\(=\dfrac{m^2+2m-15}{\left(x+m\right)^2}\)
Để hàm số đồng biến trên từng khoảng xác định là \(y'>0\forall x\in TXĐ\)
=>\(\dfrac{m^2+2m-15}{\left(x+m\right)^2}>0\)
=>\(m^2+2m-15>0\)
=>(m+5)(m-3)>0
TH1: \(\left\{{}\begin{matrix}m+5>0\\m-3>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>3\\m>-5\end{matrix}\right.\)
=>m>3
TH2: \(\left\{{}\begin{matrix}m+5< 0\\m-3< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m< -5\\m< 3\end{matrix}\right.\)
=>m<-5
b: TXĐ: D=R\{-m}
\(y=\dfrac{mx+4m}{x+m}\)
=>\(y'=\dfrac{\left(mx+4m\right)'\left(x+m\right)-\left(mx+4m\right)\left(x+m\right)'}{\left(x+m\right)^2}\)
\(=\dfrac{m\left(x+m\right)-mx-4m}{\left(x+m\right)^2}\)
\(=\dfrac{mx+m^2-mx-4m}{\left(x+m\right)^2}=\dfrac{m^2-4m}{\left(x+m\right)^2}\)
Để hàm số đồng biến trên từng khoảng xác định thì \(y'>0\forall x\)
=>\(\dfrac{m^2-4m}{\left(x+m\right)^2}>0\)
=>\(m^2-4m>0\)
=>\(m\left(m-4\right)>0\)
TH1: \(\left\{{}\begin{matrix}m>0\\m-4>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>0\\m>4\end{matrix}\right.\)
=>m>4
TH2: \(\left\{{}\begin{matrix}m< 0\\m-4< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m< 0\\m< 4\end{matrix}\right.\)
=>m<0
Đúng 0
Bình luận (0)
Cho hàm số:
y
x
-
2
x
+
3
Khẳng định nào sau đây là đúng?A. Hàm số đồng biến trên từng khoảng xác định;B. Hàm số đồng biến trên khoảng (-
∞
;+
∞
);C. Hàm số nghịch biến trên từng khoảng xác định;D. Hàm số nghịch biến trên...
Đọc tiếp
Cho hàm số: y = x - 2 x + 3
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên từng khoảng xác định;
B. Hàm số đồng biến trên khoảng (- ∞ ;+ ∞ );
C. Hàm số nghịch biến trên từng khoảng xác định;
D. Hàm số nghịch biến trên khoảng (- ∞ ;+ ∞ ).






