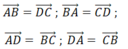Tổng của 2 vectơ đối bằng bao nhiêu

Những câu hỏi liên quan
Cho tam giác ABC. Hỏi có bao nhiêu điểm M sao cho vectơ tổng
M
A
→
+
M
B
→
+
M
C
→
có độ dài bằng 3? A. Có duy nhất một điểm B. Có hai điểm C. Có vô số điểm và tập hợp các điểm M là một đường thẳng D. Có vô số điểm và tập hợp các điểm M là một đường tròn
Đọc tiếp
Cho tam giác ABC. Hỏi có bao nhiêu điểm M sao cho vectơ tổng M A → + M B → + M C → có độ dài bằng 3?
A. Có duy nhất một điểm
B. Có hai điểm
C. Có vô số điểm và tập hợp các điểm M là một đường thẳng
D. Có vô số điểm và tập hợp các điểm M là một đường tròn
Cho ∆ABC đều cạnh bằng a , chứng minh nội tiếp đường tròn (O) . Điểm M thuộc (O) sao cho T=| vectơ MA+ vectơ MB - vectơ MC | lớn nhất. Khi đó giá trị của T bằng bao nhiêu?
Cho lục giác ABCDEF có tâm O. Số các vectơ bằng vectơ \(\overrightarrow{OC}\) có điểm đầu và điểm cuối là đỉnh của lục giác bằng bao nhiêu ?
Các véc tơ bằng véc tơ \(\overrightarrow{OC}\) có điểm đầu và điểm cuối là đỉnh lục giác là: \(\overrightarrow{FO};\overrightarrow{AB};\overrightarrow{ED}\).
Vậy có 3 véc tơ.
Đúng 0
Bình luận (0)
Cho một hình chữ nhật ABCD. Trong số các vectơ khác 0 → , có bao nhiêu cặp vectơ bằng nhau là:
A. 2
B. 4
C. 6
D. 8
Hai đội thi đấu cờ với nhau .Mỗi đối thủ của đội này phải đấu với một ván với đối thủ của đội kia. Biết rằng tổng số ván cờ đã đấu bằng 4 lần tổng số đối thủ của 2 đội và biết rằng số đối thủ của ít nhất 1 trong 2 đội là số lẻ.Hỏi mổi đội có bao nhiêu đối thủ?
cho vectơ u=vectơ a +3 vecto b vuông góc với vectơ v=7 vecto a-5 vecto b và vecto x= vecto a-4 vecto b vuông góc với vecto y=7 vecto a-2 vecto b. khi đó góc giữa 2 vecto a và b bằng bao nhiêu
Trong không gian với hệ trục tọa độ Oxyz, cho ba vectơ
u
→
1
;
1
;
2
,
a
→
3
;
-
1
;
-
2
và
v
→...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho ba vectơ u → = 1 ; 1 ; 2 , a → = 3 ; - 1 ; - 2 và v → = - 1 ; m ; m - 2 . Để vectơ u → , v → vuông góc với a → thì giá trị m bằng bao nhiêu?
A. m = 2
B. m = -2
C. m = 1
D. m = -1
Cho một đa giác đều 24 đỉnh. Hỏi: 1. Đa giác có bao nhiêu đường chéo? 2. Từ các đỉnh của đa giác, lập được bao nhiêu: a. Đoạn thẳng. b. Vectơ khác vectơ-không. c. Tam giác.
\(1,\) Đa giác có 24 đỉnh \(\Rightarrow\) Đa giác có 24 cạnh
Số đường chéo của đa giác là \(C_{24}^2-24=252\) đường chéo.
\(2,\)
\(a,\) Từ các đỉnh của đa giác, lập được \(252+24=276\) đoạn thẳng.
\(b,\) Từ các đỉnh của đa giác, lập được \(A^2_{24}=552\) vectơ khác vectơ-không.
\(c,\) Từ các đỉnh của đa giác, lập được \(C^3_{24}=2024\) tam giác.
Đúng 0
Bình luận (0)
Hai đội thi đấu cờ với nhau .Mỗi đối thủ của đội này phải đấu với một ván với đối thủ của đội kia. Biết rằng tổng số ván cờ đã đấu bằng 4 lần tổng số đối thủ của 2 đội và biết rằng số đối thủ của ít nhất 1 trong 2 đội là số lẻ.Hỏi mổi đội có bao nhiêu đối thủ?
Toán giải bằng cách lập PT: loại hai đội cùng thi đấu, mỗi người của đội này gặp một người của đội kia? | Yahoo Hỏi & Đáp
Đúng 0
Bình luận (0)
Gọi số cầu thủ đội 1 và 2 lần lượt là: a và b
1 cầu thủ đội 1 đấu với 1 cầu thủ đội 2, số trận là b
số cầu thủ đội 1 là a
=> tổng số ván đấu là: ab
=> ab=4(a+b)
=> ab chia hết cho 2
Mà ít nhất 1 đội có số cầu thủ lẻ
=> đội còn lại có số cầu thủ chẵn và chia hết cho 4, giả sử độ đó có a cầu thủ ⇒b là số lẻ
Ta có: ab=4(a+b)
⇔a(b-4)-4(b-4)=16
⇔(a-4)(b-4)=16
Vì a,b∈Z
⇒ a-4,b-4∈Z
⇒a-4,b-4 là nghiệm nguyên của 16
mà a chia hết cho 4 nên a-4 chia hết cho 4 ta xét các trương hợp:
+) \(\hept{\begin{cases}a-4=4\\b-4=4\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a=8\\b=8\end{cases}}\)
(không thoả mãn b lẻ)
+ ) \(\hept{\begin{cases}a-4=8\\b-4=2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a=12\\b=6\end{cases}}\)
(không thoả mãn b lẻ)
+)\(\hept{\begin{cases}a-4=16\\b-4=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a=20\\b=5\end{cases}}\)(thoả mãn)
Vậy mỗi đội có 20 và 5 cầu thủ