Cho tam giác ABC nhọn. AB=c, BC=a, AC=b. Chứng minh rằng a^2=b^2+c^2-2bcCosA
Cho tam giác ABC nhọn, BC=a, AC=b, AB=c. Chứng minh rằng: b2=a2+c2-2ac.cosB.
Trong tam giác vuông ACH có AC2 = AH2 + CH2 = AH2 + (BC - BH)2 = AH2 + BC2 - 2.BC.BH + BH2
Trong tam giác vuông ABH có AH2 + BH2 = AB2 và BH = AB.cosB hay BH = c.cosB
Suy ra AC2 = BC2 + AB2 - 2BC.c.cosB hay b2 = a2 + c2 - 2ac.cosB
Cho tam giác ABC nhọn, BC=a, AC=b, AB=c. Chứng minh rằng: a2=a2+c2-2ab.cosA.
Cho tam giác ABC nhọn có AB = c , AC = b , BC =a . Chứng minh rằng : \(a^2=b^2+c^2-2bc.\cos A\)
Cho tam giác ABC có góc B = góc C (góc A nhọn). Từ B hạ BH vuông góc với AC, từ C hạ CK vuông góc với AB (H thuộc AC, K thuộc AB). a) Chứng minh rằng 2 góc B và C đều nhọn b) Chứng minh rằng: BH = CK
b: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔABH=ΔACK
Cho tam giác ABC nhọn, BC= a, AC=b, AB= c
chứng minh rằng: a2 = b2 + c2 - 2bc.\(\cos A\)
từ B kẻ đường thẳng vuông góc với AC tại k
ta có: 2.AK.b=AK.b+AK.b
=AK.(AK+CK)+(b-CK).b
=AK^2+AK.CK+b^2-b.CK
=c^2-BK^2+b^2-CK.(b-AK)
=c^2-(a^2-CK^2)+b^2-CK.CK
=c^2-a^2+CK^2+b^2-CK^2
=b^2+c^2-a^2
mà: cosA=AK/c=2.AK.b/2bc
=(b^2+c^2-a^2)/2bc
=>b^2+c^2-a^2=2bc.cosA (đpcm)
Cho tam giác ABC vuông tại A đường cao AH chứng minh rằng a. Tam giác ABC đồng dạng với tam giác AC b. AB. AC = AH. BC c. 1/Ah^2 = 1/AB^2 + 1/AC^2
a) Xét tam giác ABC và tam giác HAC có:
BAC = AHC =90
ABC = HAC (cùng phụ với HAB)
=> ABC đồng dạng HAC (g.g)
b) Vì ABC đồng dạng HAC
=> AB/BC = AH/AC
=> AB.AC=BC.AH
c) Vì AB.AC = BC.AH
=> AB^2.AC^2= BC^2 . AH^2
Mà BC^2=AB^2+AC^2 (định lý pytago ở tam giác ABC vuông tại A)
=> AB^2.AC^2= (AB^2+AC)^2.AH^2
=> 1/AH^2 =1/AB^2 +1/AC^2
Cho tam giác ABC nhọn có AB=c, Ac=b, BC=a
Chứng minh S abc= 1/2bc.sin A =1/2 ac .B =1/2 ab.sin C=1/2 bc
( các bạn giúp mình nha, cám ơn nhiều)
Cho tam giác ABC có góc A = 120o, BC = a , AC= b, AB= c. Chứng minh rằng a^2 = b^2 +c^2+bc
Kẻ CE vuông góc với AB, ta có ngay tam giác ACE vuông có một góc nhọn 60. Suy ra \(AE=\frac{1}{2}AC=\frac{b}{2},CE=\frac{\sqrt{3}}{2}b\). Xét tam giác vuông EBC có '\(EB=c+\frac{b}{2},EC=\frac{\sqrt{3}}{2}b\to a^2=BC^2=BE^2+CE^2=\left(c+\frac{b}{2}\right)^2+\left(\frac{\sqrt{3}}{2}b\right)^2=c^2+bc+b^2\)
đáp án
=c2 + bc + b2
hok tót
trả lời
= c2+ bc + b2
hok tốt
Cho tam giác ABC nhọn, AB=6cm, BC=8cm.Gọi M,N theo thứ tự là trung điểm của AB và BC.
a, Chứng minh MN//AC
b, Chứng minh AM×BC=AB×BN
c,Kẻ phân giác BP(P thuộc AC) chứng minh rằng AM/CN=PA/PC
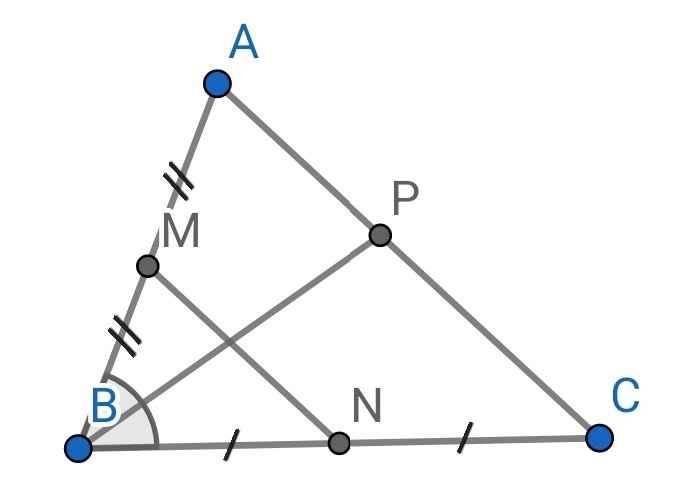 a) Do M là trung điểm của AB (gt)
a) Do M là trung điểm của AB (gt)
⇒ AM = BM = AB : 2 = 6 : 2 = 3 (cm)
Do N là trung điểm của BC (gt)
⇒ BN = CN = BC : 2 = 8 : 2 = 4 (cm)
Ta có:
BM/AM = 3/3 = 1
BN/CN = 4/4 = 1
⇒ BM/AM = BN/CN
⇒ MN // AC (định lý Ta-lét)
b) Ta có:
AM.BC = 3.8 = 24 (cm)
AB.BN = 6.4 = 24 (cm)
⇒ AM.BC = AB.BN
c) Do BP là tia phân giác của ∠ABC (gt)
⇒ BA/BC = PA/PC (1)
Do MN // AC (cmt)
⇒ BA/BC = AM/CN (2)
Từ (1) và (2) ⇒ AM/CN = PA/PC