Giải tự luận giùm mình

Những câu hỏi liên quan
Giải lý tự luận và tóm tắt giùm mình nha
Giải tin tự luận giùm
Bài 2:
#include <bits/stdc++.h>
using namespace std;
double a,b,c,delta,x1,x2;
int main()
{
//freopen("PTB2.inp","r",stdin);
//freopen("PTB2.out","w",stdout);
cin>>a>>b>>c;
delta=(b*b-4*a*c);
if (delta<0) cout<<"-1";
if (delta==0) cout<<fixed<<setprecision(5)<<(-b/(2*a));
if (delta>0)
{
x1=(-b-sqrt(delta))/(2*a);
x2=(-b+sqrt(delta))/(2*a);
cout<<fixed<<setprecision(5)<<x1<<" "<<fixed<<setprecision(5)<<x2;
}
return 0;
}
Đúng 1
Bình luận (0)
Giải ra tự luận giùm em ạ
Câu 18:
Ta có: \(3\sqrt{8a}+\dfrac{1}{4}\sqrt{\dfrac{32a}{25}}-\dfrac{a}{\sqrt{3}}\cdot\sqrt{\dfrac{3}{2a}}-\sqrt{2a}\)
\(=6\sqrt{2a}-\sqrt{2a}+\dfrac{1}{4}\cdot\dfrac{4\sqrt{2a}}{5}-\dfrac{a}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{\sqrt{2a}}\)
\(=5\sqrt{2a}+\dfrac{1}{5}\sqrt{2a}-\dfrac{1}{2}\sqrt{2a}\)
\(=\dfrac{47}{10}\sqrt{2a}\)
Chọn C
Đúng 1
Bình luận (0)
Câu 18
\(=3\sqrt{4}.\sqrt{2a}+\frac{1}{4}\sqrt{\frac{16}{25}}.\sqrt{2a}-\sqrt{\frac{a^2}{3}}.\sqrt{\frac{3}{2a}}-\sqrt{2a}\)
\(=6\sqrt{2a}+\frac{1}{5}\sqrt{2a}-\sqrt{\frac{a}{2}}-\sqrt{2a}\)
\(=6\sqrt{2a}+\frac{1}{5}\sqrt{2a}-\sqrt{\frac{1}{4}}.\sqrt{2a}-\sqrt{2a}\)
\(=6\sqrt{2a}+\frac{1}{5}\sqrt{2a}-\frac{1}{2}\sqrt{2a}-\sqrt{2a}=\frac{47}{10}\sqrt{2a}\)
Đáp án C.
Đúng 0
Bình luận (0)
Câu 19:
\(=2\sqrt{a}-\sqrt{(3a)^2}.\sqrt{a}+a\sqrt{a}.\sqrt{16}+\sqrt{\frac{4}{a^4}.36a^5}\)
\(=2\sqrt{a}-3a\sqrt{a}+4a\sqrt{a}+\sqrt{144a}\)
\(=2\sqrt{a}+a\sqrt{a}+\sqrt{144}.\sqrt{a}=2\sqrt{a}+a\sqrt{a}+12\sqrt{a}=14\sqrt{a}+a\sqrt{a}\)
Đáp án A.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giúp toán tự luận giùm mình
Câu 1:
\(f\left(-x\right)=\left(-x\right)^4-3\cdot\left(-x\right)^2+1\)
\(=x^4-3x^2+1=f\left(x\right)\)
Vậy: f(x) là hàm số chẵn
Đúng 1
Bình luận (1)
\(c1:D=R\Rightarrow\forall x\in D\Rightarrow-x\in D\)
\(\Rightarrow f\left(-x\right)=x^4-3x^2+1=f\left(x\right)\Rightarrow hàm\) \(số\) \(chẵn\)
\(c2:cm:\overrightarrow{AC}+\overrightarrow{BD}=2\overrightarrow{MN}\)
\(M,N\) \(trung\) \(điểm\) \(AB,CD\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}\\\overrightarrow{DN}+\overrightarrow{CN}=\overrightarrow{0}\end{matrix}\right.\)
\(\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CN}\)
\(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{DN}\)
\(\Rightarrow2\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{MA}+\overrightarrow{BC}+\overrightarrow{AD}+\overrightarrow{CN}+\overrightarrow{DN}\)
\(=\overrightarrow{0}+\overrightarrow{BC}+\overrightarrow{AD}+\overrightarrow{0}\Rightarrow2\overrightarrow{MN}=\overrightarrow{AD}+\overrightarrow{BC}\left(đpcm\right)\)
\(c3:D=R\text{[}-5;\text{+∞.)}\)
\(f\left(x\right)\) \(nghịch\) \(biến\Leftrightarrow a< 0\)
\(\Rightarrow-5\le a< 0\left(a\in Z\right)\Rightarrow a=\left\{-5;-4;-3;-2;-1\right\}\)
\(c4:\) có công thức \(X\cap Y=X+Y-X\cup Y=25+20-36=9\)
Đúng 0
Bình luận (0)


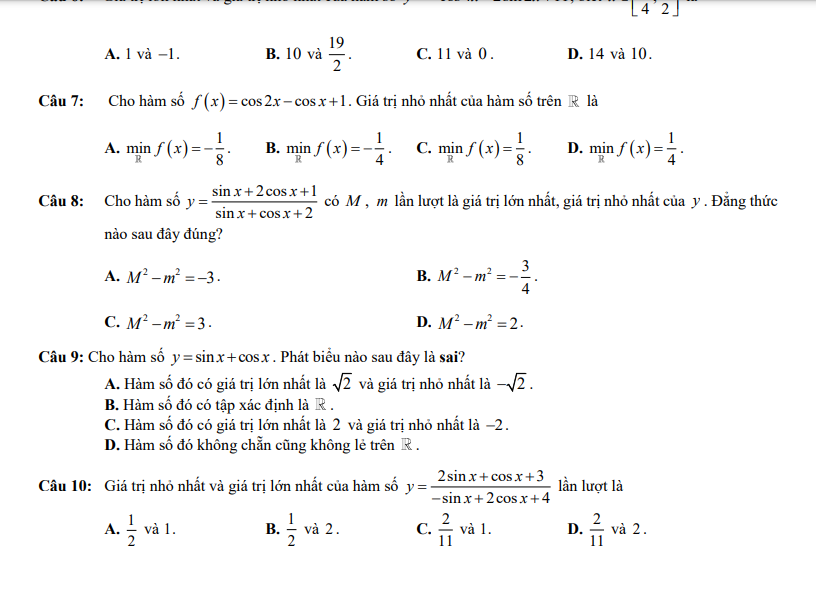
giải giùm em theo kiểu tự luận ạ
1.
\(2sinx+cosx=4\)
\(\Leftrightarrow\sqrt{5}\left(\dfrac{2}{\sqrt{5}}sinx+\dfrac{1}{\sqrt{5}}cosx\right)=4\)
\(\Leftrightarrow sin\left(x+arccos\dfrac{2}{\sqrt{5}}\right)=\dfrac{4}{\sqrt{5}}>1\)
\(\Rightarrow2sinx+4cosx-4\ne0\)
Khi đó:
\(2P.sinx+P.cosx-4P=sinx-2cosx-3\)
\(\Leftrightarrow\left(2P-1\right)sinx+\left(P+2\right)cosx=4P-3\)
Phương trình có nghiệm khi:
\(\left(2P-1\right)^2+\left(P+2\right)^2\ge\left(4P-3\right)^2\)
\(\Leftrightarrow4P^2-4P+1+P^2+4P+4\ge16P^2+9-24P\)
\(\Leftrightarrow11P^2-24P+4\le0\)
\(\Leftrightarrow\dfrac{2}{11}\le P\le2\)
\(\Rightarrow maxP=2\)
Đúng 2
Bình luận (0)
Để đánh số trang của một cuốn sách có 136 trang cần dùng tất cả bao nhiêu chữ số 2? Giải tự luận giùm mình cảm ơn mọi người nhiều!
tải quanda về nha
chỉ giùm mình 2-3-4 tự luận vs ạ
Mọi người ơi, giúp mình với! Mình năm nay lớp 5 và gặp 1 bài toán tự luận khó, mong mọi người giải giùm mình với.
Đồng hồ đang chỉ vào khoảng 8h 20 phút. Biết rằng khoảng cách từ kim giờ đến số 6 bằng khoảng cách từ kim phút đến số 6. Tính chính xác giờ mà đồng hồ đang chỉ?
Nếu có ai giải được bằng tự luận thì RẤT CẢM ƠN
Giúp mk với mn ơi phần tự luận mn giải chi tiết ra giùm mk ạ cảm ơn mn nhiều 😘😘
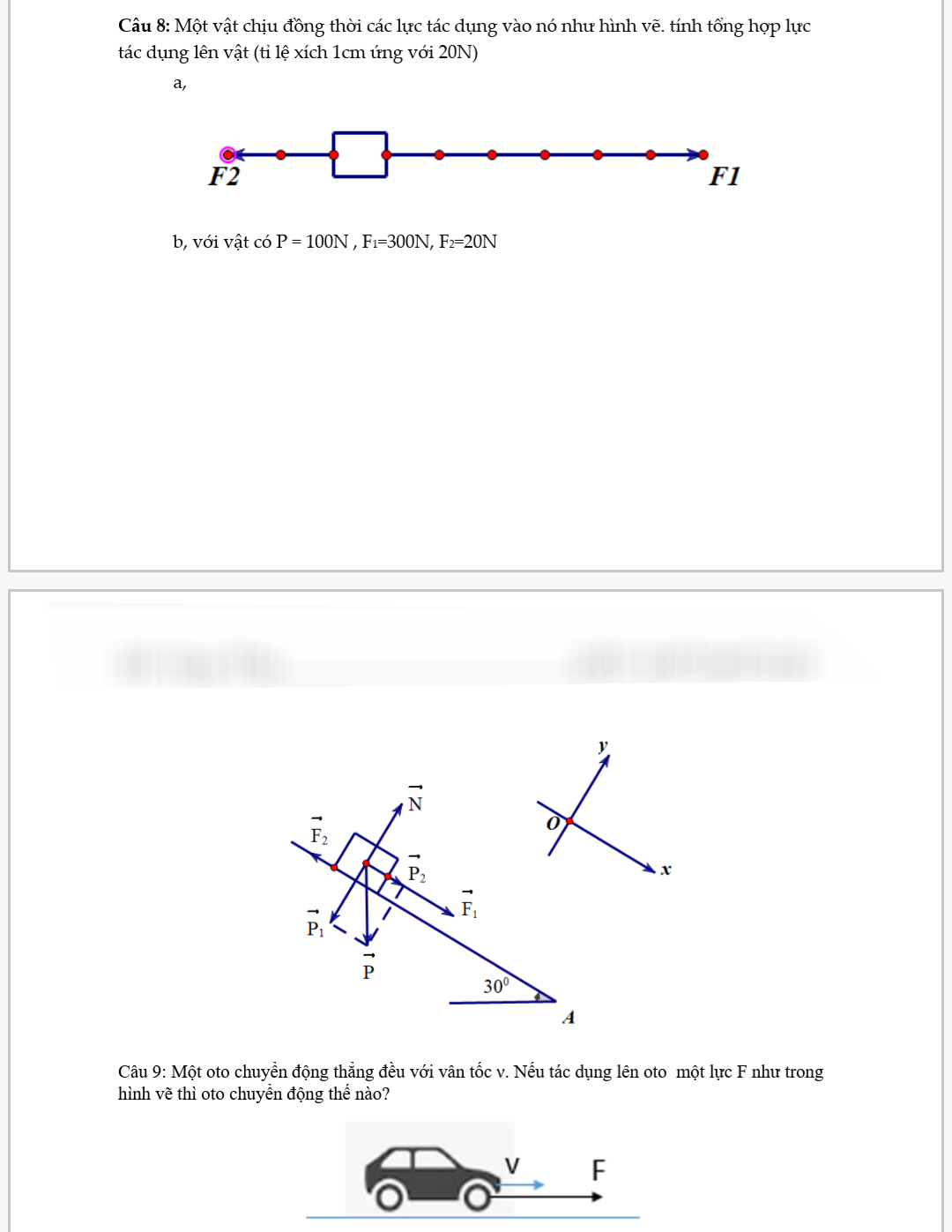

Bạn nên đăng những câu khó nhất hoặc bạn lọc ra những câu tương tự nhau để bản thân có thể vận dụng nhé!
Đúng 1
Bình luận (1)















