Chứng minh rằng đồ thị hàm số y = \(x+2-\frac{1}{x-1}\) nhận I(1;3) làm tâm đối xứng.

Những câu hỏi liên quan
Cho hàm số
f
x
3
x
+
2
n
ế
u
x
-
1...
Đọc tiếp
Cho hàm số f x = 3 x + 2 n ế u x < - 1 x 2 - 1 n ế u x ≥ - 1
a. Vẽ đồ thị hàm số y= f(x). Từ đó nêu nhận xét vê tính liên tục của hàm số trên tập xác định của nó.
b. Khẳng định nhận xét trên bằng 1 chứng minh.
a) Đồ thị hàm số (hình bên).
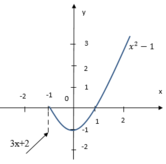
Quan sát đồ thị nhận thấy :
+ f(x) liên tục trên các khoảng (-∞ ; -1) và (-1 ; ∞).
+ f(x) không liên tục tại x = -1.
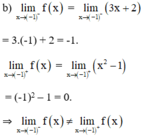
⇒ không tồn tại giới hạn của f(x) tại x = -1.
⇒ Hàm số không liên tục tại x = -1.
Đúng 0
Bình luận (0)
Câu 1: Cho tỉ lệ thức a/b=c/d chứng minh rằng (2a+3b)/(2a-3b)=(2c+3d)=(2c-3d)
Câu 2: Cho hàm số y=-1/3.x và hàm số y=x-4
1)Vẽ đồ thị hàm số y=-1/3.x
2)Chứng tỏ M(3;-1) là giao của hai đồ thị hàm số trên
3)Tìm độ dài OM(O là gốc tọa độ)
Cho hàm số y=f(x)=-m+4
- tìm m để đồ thị hàm số đi qua điểm A (-1;1)
- Chứng minh rằng đồ thị hàm số chỉ đi qua 1 điểm cố định với mọi m.
Thay x=-1 và y=1 vào f(x), ta được:
m+4=1
hay m=-3
Đúng 2
Bình luận (1)
1)Cho hàm số y = ax
-Hãy xác định hệ số a biết đồ thị của hàm số đã cho đi qua điểm A (-2;1) -Vẽ đồ thị của hàm số đã cho với a vừa tìm được 2) Hàm số y = f(x) được cho bởi công thức f(x) = 3x² + 5. Chứng minh rằng bới mọi giá trị của x thì hàm số đã cho luôn nhận giá trị dương.Bài 2:
\(3x^2+5\ge5>0\forall x\)
nên f(x)>0 với mọi x
Đúng 0
Bình luận (0)
Cho hàm số bậc nhất y=(2m-1)x+m-3. Tìm m để hàm số bậc nhất đi qua 2 điểm có tọa độ 2,5. Tìm m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ = căn 2 -1. Chứng minh rằng đồ thị hàm số luôn đi qua 1 điểm cố định với mọi m.
I. Cho hàm số y x3 - 2x2 + x - 1 có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị hàm số (C), biết rằng đồ thị này song song với đường thẳng y -5x + 17.
II. Xét tính liên tục của hàm số sau:
left{{}begin{matrix}dfrac{-x^2+2x+1}{-x-1}|khix-13-2x|khix1end{matrix}right.tại x0 1
III. Cho hình chóp S.ABCD có SA perp (ABCD), ABCD là hình chữ nhật. Chứng minh rằng BC perp (SAC).
Giải giúp mình nhé. Mai mình thi HKII rồi. Cảm ơn các bạn rất nhiều.
Đọc tiếp
I. Cho hàm số y = x3 - 2x2 + x - 1 có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị hàm số (C), biết rằng đồ thị này song song với đường thẳng y = -5x + 17.
II. Xét tính liên tục của hàm số sau:
\(\left\{{}\begin{matrix}\dfrac{-x^2+2x+1}{-x-1}|khix=-1\\3-2x|khix=1\end{matrix}\right.\)tại x0 = 1
III. Cho hình chóp S.ABCD có SA \(\perp\) (ABCD), ABCD là hình chữ nhật. Chứng minh rằng BC \(\perp\) (SAC).
Giải giúp mình nhé. Mai mình thi HKII rồi. Cảm ơn các bạn rất nhiều.
Cho hàm số \(y=mx+m-6\left(m\ne0\right)\left(1\right)\).
1) Xác định m biết đồ thị hàm số (1) đi qua điểm M(2; 3). Vẽ đồ thị hàm số (1) với m vừa tìm được.
2) Tìm m để đồ thị hàm số (1) song song với đường thẳng \(y=3x+2\)
3) Chứng minh rằng đồ thị hàm số (1) luôn đi qua một điểm cố định với mọi giá trị của tham số m
1. Đồ thị của hàm số đi qua điểm \(M\left(2;3\right)\) nên giá trị hoành độ và tung độ của \(M\) là nghiệm của phương trình đường thẳng trên, tức:
\(3=m\cdot2+m-6\Leftrightarrow m=3\left(TM\right)\)
2. Đồ thị hàm số song song với đường thẳng \(\left(d\right):y=3x+2\), khi: \(\left\{{}\begin{matrix}m=3\\m-6\ne2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\m\ne8\end{matrix}\right.\Rightarrow m=3\left(TM\right)\)
3. Gọi \(P\left(x_0;y_0\right)\) là điểm cố định mà đồ thị hàm số đi qua với mọi giá trị \(m\).
Khi đó: \(mx_0+m-6=y_0\Leftrightarrow\left(x_0+1\right)m-\left(y_0+6\right)=0\left(I\right)\)
Suy ra, phương trình \(\left(I\right)\) có vô số nghiệm, điều này xảy ra khi: \(\left\{{}\begin{matrix}x_0+1=0\\y_0+6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=-1\\y_0=-6\end{matrix}\right.\).
Vậy: Điểm cố định mà đồ thị hàm số luôn đi qua với mọi giá trị \(m\) là \(P\left(-1;-6\right)\).
Đúng 4
Bình luận (0)
cho 2 hàm số y = -2x + 4 (1)
y = \(\frac{1}{2}x+\frac{3}{2}\left(2\right)\)
Gọi đồ thị (1) giao với Ox; Oy lần lượt tại M,N . Đồ thị (2) giáo với Ox; Oy lần lượt tại I và K. Chứng minh rằng MN vuông góc với IK
Cho đồ thị hàm số \(y=-\frac{1}{3}x\)và hàm số y=x-4
Vẽ đồ thị hàm số y=-1/3x
chứng torM(3;-1) là giao của hai đồ thị hàm số trên
Tính độ dài OM( O là gốc tọa độ)
Giao điểm 2 đồ thị
y=-x/3 và y=x-4
=> -x/3 = x - 4
=> -x = 3x - 12
=> x = 3
Thay x = 3 vào 1 trong 2 hàm số => y = -1
=> M(3,-1) Là giao điểm 2 đồ thị.
OM = \(\sqrt{3^2+\left(-1\right)^2}\) = \(\sqrt{10}\)
Đúng 0
Bình luận (0)
¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿¿

















