a: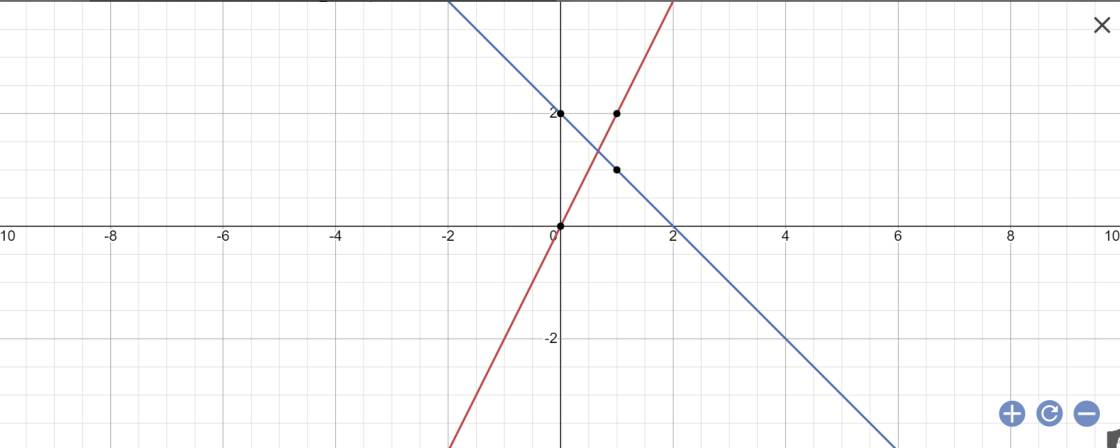 

b: Vì (d3)//(d2) nên \(\left\{{}\begin{matrix}a=-1\\b\ne2\end{matrix}\right.\)

Vậy: (d3): y=-x+b

Thay x=1 vào (d1), ta được:

\(y=2\cdot1=2\)

Thay x=1 và y=2 vào y=-x+b, ta được:

\(b-1=2\)

=>b=2+1=3

b) Vì A(xA;yA) là giao điểm của (D) và (D1) nên Hoành độ của A là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của (D) và (D1)

hay \(-x-4=3x+2\)

\(\Leftrightarrow-x-4-3x-2=0\)

\(\Leftrightarrow-4x-6=0\)

\(\Leftrightarrow-4x=6\)

hay \(x=-\dfrac{3}{2}\)

Thay \(x=-\dfrac{3}{2}\) vào hàm số y=-x-4, ta được: 

\(y=-\left(-\dfrac{3}{2}\right)-4=\dfrac{3}{2}-4=\dfrac{3}{2}-\dfrac{8}{2}=-\dfrac{5}{2}\)

Vậy: \(A\left(-\dfrac{3}{2};-\dfrac{5}{2}\right)\)

c) Vì (D2) song song với (D) nên a=-1

hay (D2): y=-x+b

Vì (D2) đi qua điểm B(-2;5)

nên Thay x=-2 và y=5 vào hàm số y=-x+b, ta được: 

-(-2)+b=5

hay b=5-2=3

Vậy: (D2): y=-x+3

b) Vì A(xA;yA) là giao điểm của (D) và (D1) nên Hoành độ của A là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của (D) và (D1)

hay \(-x-4=3x+2\)

\(\Leftrightarrow-x-4-3x-2=0\)

\(\Leftrightarrow-4x-6=0\)

\(\Leftrightarrow-4x=6\)

hay \(x=-\dfrac{3}{2}\)

Thay \(x=-\dfrac{3}{2}\) vào hàm số y=-x-4, ta được: 

\(y=-\left(-\dfrac{3}{2}\right)-4=\dfrac{3}{2}-4=\dfrac{3}{2}-\dfrac{8}{2}=-\dfrac{5}{2}\)

Vậy: \(A\left(-\dfrac{3}{2};-\dfrac{5}{2}\right)\)

c) Vì (D2) song song với (D) nên a=-1

hay (D2): y=-x+b

Vì (D2) đi qua điểm B(-2;5)

nên Thay x=-2 và y=5 vào hàm số y=-x+b, ta được: 

-(-2)+b=5

hay b=5-2=3

Vậy: (D2): y=-x+3

b) Vì A(xA;yA) là giao điểm của (D) và (D1) nên Hoành độ của A là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của (D) và (D1)

hay \(-x-4=3x+2\)

\(\Leftrightarrow-x-4-3x-2=0\)

\(\Leftrightarrow-4x-6=0\)

\(\Leftrightarrow-4x=6\)

hay \(x=-\dfrac{3}{2}\)

Thay \(x=-\dfrac{3}{2}\) vào hàm số y=-x-4, ta được: 

\(y=-\left(-\dfrac{3}{2}\right)-4=\dfrac{3}{2}-4=\dfrac{3}{2}-\dfrac{8}{2}=-\dfrac{5}{2}\)

Vậy: \(A\left(-\dfrac{3}{2};-\dfrac{5}{2}\right)\)

c) Vì (D2) song song với (D) nên a=-1

hay (D2): y=-x+b

Vì (D2) đi qua điểm B(-2;5)

nên Thay x=-2 và y=5 vào hàm số y=-x+b, ta được: 

-(-2)+b=5

hay b=5-2=3

Vậy: (D2): y=-x+3

Cách 1:

Do M thuộc d, gọi tọa độ M có dạng \(M\left(2m-2;m\right)\)

\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(2m-2;m-6\right)\\\overrightarrow{BM}=\left(2m-4;m-5\right)\end{matrix}\right.\)

Đặt \(T=MA+MB=\sqrt{\left(2m-2\right)^2+\left(m-6\right)^2}+\sqrt{\left(2m-4\right)^2+\left(m-5\right)^2}\)

\(T=\sqrt{5m^2-20m+40}+\sqrt{5m^2-26m+41}\)

\(T=\sqrt{5\left(m-2\right)^2+\left(2\sqrt{5}\right)^2}+\sqrt{5\left(\dfrac{13}{5}-m\right)^2+\left(\dfrac{6}{\sqrt{5}}\right)^2}\)

\(T\ge\sqrt{5\left(m-2+\dfrac{13}{5}-m\right)^2+\left(2\sqrt{5}+\dfrac{6}{\sqrt{5}}\right)^2}=\sqrt{53}\)

Dấu "=" xảy ra khi và chỉ khi:

\(6\left(m-2\right)=10\left(\dfrac{13}{5}-m\right)\Leftrightarrow m=\dfrac{19}{8}\)

\(\Rightarrow M\left(\dfrac{11}{4};\dfrac{19}{8}\right)\)

Cách 2:

Thay tọa độ A và B vào pt (d) được 2 giá trị cùng dấu âm \(\Rightarrow A;B\) nằm cùng phía so với (d)

Gọi d' là đường thẳng qua A và vuông góc với d \(\Rightarrow\) pt d' có dạng:

\(2\left(x-0\right)+1\left(y-6\right)=0\Leftrightarrow2x+y-6=0\)

Gọi C là giao điểm của d và d' \(\Rightarrow\left\{{}\begin{matrix}x-2y+2=0\\2x+y-6=0\end{matrix}\right.\)

\(\Rightarrow C\left(2;2\right)\)

Gọi D là điểm đối xứng với A qua d \(\Leftrightarrow C\) là trung điểm AD \(\Rightarrow D\left(4;-2\right)\)

Phương trình BD có dạng: \(7\left(x-2\right)+2\left(y-5\right)=0\Leftrightarrow7x+2y-24=0\)

\(MA+MB\) nhỏ nhất khi và chỉ khi M là giao điểm của BD

\(\Rightarrow\) Tọa độ M thỏa mãn: \(\left\{{}\begin{matrix}7x+2y-24=0\\x-2y+2=0\end{matrix}\right.\) \(\Rightarrow M\left(\dfrac{11}{4};\dfrac{19}{8}\right)\)

b) Xét tam giác OMB vuông tại O có:

BM2 = OM2 + OB2 = 1 + 1 = 2 ⇒ BM = √2

Tương tự tam giác OAB vuông tại O có:

B A 2  = O A 2 + O B 2  = 1 + 1 = 2 ⇒ BA = 2

Xét tam giác MAB có:

B M 2 + B A 2  = 2 + 2 = 4 = A M 2

⇒ ΔMAB vuông tại B

Do đó, khoảng cách từ M đến đường thẳng (d) là độ dài đoạn BM = 2

Đồ thị của hàm số y = ax ( a ≠ 0 ) là đường thẳng OA đi qua điểm A(-1;-3) do đó khi x = -1thì y = -3

Nên ta có -3 = a.(-1) => a = 3  (TM)
Công thức của hàm số đã cho là: y = 3x.

Đáp án cần chọn là: D