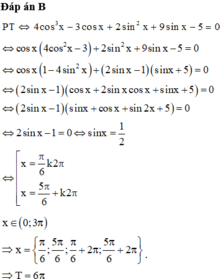Giải phương trình sau: \(cos3x+cos2x+sin^2x=2\)

Những câu hỏi liên quan
giải các phương trình sau :1. sin( x+pi/4)2/32.cos2x-5sinx-303.cos3xsin2x4.cos3x-sqrt{ }3 với -pi/2x05.4sin^4x + 12cos^2x76.cot(x-1)(cos2x)/(1+tanx) + sin^2x - 1/2sin2x7.sin^23x-cos^24xsin^25x-cos^26x
Đọc tiếp
giải các phương trình sau :
1. sin( x+\(\pi\)/4)=2/3
2.cos2x-5sinx-3=0
3.cos3x=sin2x
4.cos3x=-\(\sqrt{ }\)3 với -\(\pi\)/2<x<0
5.4sin\(^4\)x + 12cos\(^2\)x=7
6.cot(x-1)=(cos2x)/(1+tanx) + sin\(^2\)x - 1/2sin2x
7.sin\(^2\)3x-cos\(^2\)4x=sin\(^2\)5x-cos\(^2\)6x
Giải các phương trình sau
a) \(sin^6x+cos^6x=cos2x+\dfrac{1}{16}\)
b) \(sin^4\dfrac{x}{2}+cos^4\dfrac{x}{2}=\dfrac{5}{2}-2sinx\)
c) \(cos5xcosx=cos4xcos2x+4-3sin^2x\)
d) \(2cosxcos2x=1+cos2x+cos3x\)
e) \(sin3x+cos2x=2\left(sin2xcosx-1\right)\)
a.
\(\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)=cos2x+\dfrac{1}{16}\)
\(\Leftrightarrow1-\dfrac{3}{4}sin^22x=cos2x+\dfrac{1}{16}\)
\(\Leftrightarrow\dfrac{15}{16}-\dfrac{3}{4}\left(1-cos^22x\right)=cos2x\)
\(\Leftrightarrow\dfrac{3}{4}cos^22x-cos2x+\dfrac{3}{16}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=\dfrac{4-\sqrt{7}}{6}\\cos2x=\dfrac{4+\sqrt{7}}{6}>1\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow x=\pm\dfrac{1}{2}arccos\left(\dfrac{4-\sqrt{7}}{6}\right)+k\pi\)
Đúng 1
Bình luận (0)
b.
\(\left(sin^2\dfrac{x}{2}+cos^2\dfrac{x}{2}\right)^2-2sin^2\dfrac{x}{2}cos^2\dfrac{x}{2}=\dfrac{5}{2}-2sinx\)
\(\Leftrightarrow1-\dfrac{1}{2}sin^2x=\dfrac{5}{2}-2sinx\)
\(\Leftrightarrow\dfrac{1}{2}sin^2x-2sinx+\dfrac{3}{2}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=1\\sinx=3\left(loại\right)\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\)
Đúng 0
Bình luận (0)
c.
\(\Leftrightarrow\dfrac{1}{2}cos6x+\dfrac{1}{2}cos4x=\dfrac{1}{2}cos6x+\dfrac{1}{2}cos2x+4-3\left(\dfrac{1}{2}-\dfrac{1}{2}cos2x\right)\)
\(\Leftrightarrow\dfrac{1}{2}\left(2cos^22x-1\right)=\dfrac{1}{2}cos2x+\dfrac{5}{2}+\dfrac{3}{2}cos2x\)
\(\Leftrightarrow cos^22x-2cos2x-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=-1\\cos2x=3\left(loại\right)\end{matrix}\right.\)
\(\Leftrightarrow2x=\pi+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải các phương trình
a) \(\dfrac{\cos2x}{\sin2x-1}=0\)
b) \(\cos\left(\sin x\right)=1\)
c) \(2\sin^2x-1+\cos3x=0\)
d) \(tan3x.tanx=1\)
e) \(\cos3x=-\cos7x\)
a: ĐKXĐ: sin 2x<>1
=>2x<>pi/2+k2pi
=>x<>pi/4+kpi
\(\dfrac{cos2x}{sin2x-1}=0\)
=>cos2x=0
=>2x=pi/2+kpi
=>x=pi/4+kpi/2
Kết hợp ĐKXĐ, ta được:
x=3/4pi+k2pi hoặc x=7/4pi+k2pi
b: cos(sinx)=1
=>sin x=kpi
=>sin x=0
=>x=kpi
c: \(2\cdot sin^2x-1+cos3x=0\)
=>cos3x+cos2x=0
=>cos3x=-cos2x=-sin(pi/2-2x)=sin(2x-pi/2)
=>cos3x=cos(pi/2-2x+pi/2)=cos(pi-2x)
=>3x=pi-2x+k2pi hoặc 3x=-pi+2x+k2pi
=>x=-pi+k2pi hoặc x=pi/5+k2pi/5
e: cos3x=-cos7x
=>cos3x=cos(pi-7x)
=>3x=pi-7x+k2pi hoặc 3x=-pi+7x+k2pi
=>x=pi/10+kpi/5 hoặc x=pi/4-kpi/2
Đúng 2
Bình luận (0)
1+cosx+cos2x+cos3x=0
sinx+sin3x+sin5x=cosx+cos3x+cos5x
sin^2x + sin^2(3x) = 2sin^2(2x)
mọi người giúp mình giải phương trình này với mình cảm ơn
a/
\(\Leftrightarrow1+cos2x+cos3x+cosx=0\)
\(\Leftrightarrow2cos^2x+2cos2x.cosx=0\)
\(\Leftrightarrow2cosx\left(cosx+cos2x\right)=0\)
\(\Leftrightarrow2cosx\left(2cos^2x+cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=-1\\cosx=\frac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow...\)
b/
\(\Leftrightarrow2sin3x.cosx+sin3x=2cos3x.cosx+cos3x\)
\(\Leftrightarrow sin3x\left(2cosx+1\right)-cos3x\left(2cosx+1\right)=0\)
\(\Leftrightarrow\left(sin3x-cos3x\right)\left(2cosx+1\right)=0\)
\(\Leftrightarrow\sqrt{2}sin\left(3x-\frac{\pi}{4}\right)\left(2cosx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(3x-\frac{\pi}{4}\right)=0\\cosx=-\frac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow...\)
Đúng 0
Bình luận (0)
c/
\(\Leftrightarrow\frac{1}{2}-\frac{1}{2}cos2x+\frac{1}{2}-\frac{1}{2}cos6x=1-cos4x\)
\(\Leftrightarrow cos6x+cos2x-2cos4x=0\)
\(\Leftrightarrow2cos4x.cos2x-2cos4x=0\)
\(\Leftrightarrow2cos4x\left(cos2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos4x=0\\cos2x=1\end{matrix}\right.\) \(\Leftrightarrow...\)
giải phương trình: \(\frac{\cos x}{\cos3x}-\frac{\cos5x}{\cos x}+8\sin^2\left(2x+\frac{11\pi}{2}\right)=4\left(1+\cos2x\right)\)
ĐKXĐ: \(x\ne\frac{\pi}{6}+\frac{k\pi}{3}\)
\(\Leftrightarrow\frac{cos^2x-cos3x.cos5x}{cos3x.cosx}-4\left[1-2sin^2\left(2x+\frac{11\pi}{2}\right)\right]-4cos2x=0\)
\(\Leftrightarrow\frac{2cos^2x-cos2x-cos8x}{cos4x+cos2x}-4cos\left(4x+11\pi\right)-4cos2x=0\)
\(\Leftrightarrow\frac{1-cos8x}{cos4x+cos2x}+4cos4x-4cos2x=0\)
\(\Leftrightarrow1-cos8x+4\left(cos4x-cos2x\right)\left(cos4x+cos2x\right)=0\)
\(\Leftrightarrow1-cos8x+4cos^24x-4cos^22x=0\)
\(\Leftrightarrow1-\left(2cos^24x-1\right)+4cos^24x-2\left(1+cos4x\right)=0\)
\(\Leftrightarrow cos^24x-cos4x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos4x=0\\cos4x=1\end{matrix}\right.\) \(\Leftrightarrow...\)
Đúng 0
Bình luận (0)
Giải phương trình sau: \(\cot x-1=\dfrac{\cos2x}{1+\tan x}+\sin^2x-\dfrac{1}{2}\sin2x\)
ĐKXĐ: \(x\ne\dfrac{k\pi}{2}\)
\(\dfrac{cosx}{sinx}-1=\dfrac{cos^2x-sin^2x}{1+\dfrac{sinx}{cosx}}+sin^2x-sinx.cosx\)
\(\Leftrightarrow\dfrac{cosx-sinx}{sinx}=cosx\left(cosx-sinx\right)-sinx\left(cosx-sinx\right)\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(\dfrac{1}{sinx}-cosx+sinx\right)=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(1-sinx.cosx+sin^2x\right)=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(3-sin2x-cos2x\right)=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(3-\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\right)=0\)
Đúng 0
Bình luận (0)
Giải phương trình sau:
cos
3
x
+
3
cos
2
x
+
2
cos
x
0
Đọc tiếp
Giải phương trình sau: cos 3 x + 3 cos 2 x + 2 cos x = 0
![]()
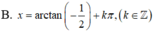
![]()
![]()
giải các phương trình : a) \(\sin x+\sin2x+\sin3x=\cos x+\cos2x+\cos3x\) ; b) \(\sin x=\sqrt{2}\sin5x-\cos x\) ; c) \(\frac{1}{\sin2x}+\frac{1}{\cos2x}=\frac{2}{\sin4x}\) ; d)
\(\sin x+\cos x=\frac{\cos2x}{1-\sin2x}\)
Phương trình cos3x – cos2x + 9.sin x – 4 0 trên khoảng
0
,
3
π
có tổng các nghiệm là
Đọc tiếp
Phương trình cos3x – cos2x + 9.sin x – 4 = 0 trên khoảng 0 , 3 π có tổng các nghiệm là
![]()
![]()
![]()
![]()