Các bạn cho tui hỏi, muốn kết luận tập xác định của hàm số mà có dương vô cực (hay âm vô cực) thì kết luận như nào?

Những câu hỏi liên quan
Cho hàm số
f
(
x
)
1
/
(
x
-
2
)
có đồ thị như ở Hình 52Quan sát đồ thị và cho biết:- Khi biến x dần tới dương vô cực, thì f(x) dần tới giá trị nào. - Khi biến x dần tới âm vô cực, thì f(x) dần tới giá trị nào.
Đọc tiếp
Cho hàm số f ( x ) = 1 / ( x - 2 ) có đồ thị như ở Hình 52
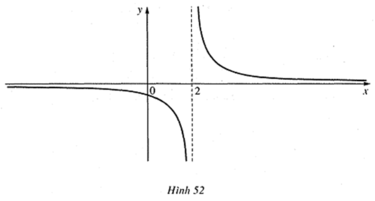
Quan sát đồ thị và cho biết:
- Khi biến x dần tới dương vô cực, thì f(x) dần tới giá trị nào.
- Khi biến x dần tới âm vô cực, thì f(x) dần tới giá trị nào.
- Khi biến x dần tới dương vô cực, thì f(x) dần tới giá trị 0.
- Khi biến x dần tới âm vô cực, thì f(x) dần tới giá trị 0.
Đúng 0
Bình luận (0)
Xét sự biến thiên của hàm số f(x)=x+1x1x trên khoảng (1; dương vô cực). Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng (1; dương vô cực)
B. Hàm số nghịch biến trên khoảng (1; dương vô cực)
C. Hàm số đồng biến trên khoảng (-1;1)
D. Hàm số nghịch biến trên khoảng (âm vô cực; 1)
Mọi người giải ra giúp mình với ạ
Cho hàm số \(f\left( x \right) = x\) có đồ thị như ở Hình 9. Quan sát đồ thị đó và cho biết:
a) Khi biến x dần tới dương vô cực thì \(f\left( x \right)\) dần tới đâu.
b) Khi biến x dần tới âm vô cực thì \(f\left( x \right)\) dần đâu.
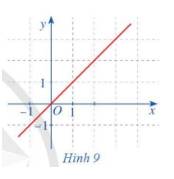
a) Khi biến x dần tới dương vô cực thì \(f\left( x \right)\) dần tới dương vô cực.
b) Khi biến x dần tới âm vô cực thì \(f\left( x \right)\) dần âm vô cực.
Đúng 0
Bình luận (0)
Cho hàm số \(f\left( x \right) = \frac{1}{x}\,\,\left( {x \ne 0} \right)\) có đồ thị như ở Hình 7. Quan sát đồ thị đó và cho biết:
a) Khi biến x dần tới dương vô cực thì \(f\left( x \right)\) dần tới giá trị nào.
b) Khi biến x dần tới âm vô cực thì \(f\left( x \right)\) dần tới giá trị nào.
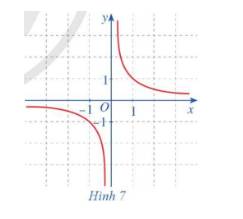
a) Khi biến x dần tới dương vô cực thì \(f\left( x \right)\) dần tới 0.
b) Khi biến x dần tới âm vô cực thì \(f\left( x \right)\) dần tới 0.
Đúng 0
Bình luận (0)
Cho hàm số
y
2
x
3
+
3
x
2
-
12
x
+
2019
. Gọi
x
1
và
x
2
lần lượt là điểm cực đại và cực tiểu của hàm số. Kết luận nào sau đây là đúng
Đọc tiếp
Cho hàm số y = 2 x 3 + 3 x 2 - 12 x + 2019 . Gọi x 1 và x 2 lần lượt là điểm cực đại và cực tiểu của hàm số. Kết luận nào sau đây là đúng
![]()
![]()
![]()
![]()
Cho bài toán: “Xét tính đơn điệu của hàm số
y
x
2
+
2
x
-
3
” Một bạn học sinh đã làm bài như sau:Bước 1: Tập xác định:
D
ℝ
(
-
3
;
1
)
Bước 2: Tìm đạo hàm:
y
x
2...
Đọc tiếp
Cho bài toán: “Xét tính đơn điệu của hàm số y = x 2 + 2 x - 3 ” Một bạn học sinh đã làm bài như sau:
Bước 1: Tập xác định: D = ℝ \ ( - 3 ; 1 )
Bước 2: Tìm đạo hàm: y ' = x 2 + 2 x - 3 ' 2 x 2 + 2 x - 3 = x + 1 x 2 + 2 x - 3
Bước 3: y ' = 0 ⇔ x + 1 = 0 x 2 + 2 x - 3 > 0 ⇔ x = 1 x < - 3 ⇔ x ∈ ∅ ; x > 1
Bước 4: Bảng biến thiên:
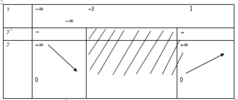
Bước 5: Kết luận:
Vậy hàm số nghịch biến trên nửa khoảng ( - ∞ ; - 3 ] , đồng biến trên nửa khoảng [ 1 ; + ∞ ) . Hỏi bài làm trên đúng hay
sai? Nếu sai thì sai từ bước nào?
A. Bài làm đúng.
B. Sai từ bước 3.
C. Sai từ bước 4.
D. Sai từ bước 5
Số bội giác của kính hiển vi ngắm chừng ở vô cực có (các) tính chất nào sau đây ?
A. Tỉ lệ thuận với tiêu cự vật kính.
B. Tỉ lệ thuận với tiêu cự thị kính.
C. Tỉ lệ thuận với độ dài quang học của kính.
D. Các kết luận A, B, C đều đúng.
Cho hàm số y 2x3 + 3x2 – 12x - 12. Gọi x1, x2 lần lượt là hoành độ hai điểm cực đại và cực tiểu của đồ thị hàm số. Kết luận nào sau đây là đúng? A. (x1 – x2)2 8 B. x1x2 2 C. x2 – x1 3 D. x12 + x22 6
Đọc tiếp
Cho hàm số y = 2x3 + 3x2 – 12x - 12. Gọi x1, x2 lần lượt là hoành độ hai điểm cực đại và cực tiểu của đồ thị hàm số. Kết luận nào sau đây là đúng?
A. (x1 – x2)2 = 8
B. x1x2 = 2
C. x2 – x1 = 3
D. x12 + x22 = 6
Đáp án C.
TXĐ: D = R.
Ta có y’ = 6x2 + 6x - 12, y’ = 0 ó 6x2 + 6x – 12 = 0 ó x = 1 hoặc x = -2.
y’’ = 12x + 12, y’’(1) = 24 > 0 => x2 = 1 là điểm cực tiểu, y’’(-2) = -12 < 0 => x1 - 2 là điểm cực đại.
Vậy ta có x2 – x1 = 3.
Đúng 0
Bình luận (0)
Kết luận nào đúng về cực trị của hàm số y x3 – 3x2 + 3x + 4 A. Đạt cực đại tại x 1 B. Có hai điểm cực trị C. Đạt cực tiểu tại x 1 D. Không có cực trị
Đọc tiếp
Kết luận nào đúng về cực trị của hàm số y = x3 – 3x2 + 3x + 4
A. Đạt cực đại tại x = 1
B. Có hai điểm cực trị
C. Đạt cực tiểu tại x = 1
D. Không có cực trị
Đáp án D.
Ta có y’ = 3(x – 1)2 ≥ 0, ∀x ∈ R
Đúng 0
Bình luận (0)










