a) Khi biến x dần tới dương vô cực thì \(f\left( x \right)\) dần tới 0.
b) Khi biến x dần tới âm vô cực thì \(f\left( x \right)\) dần tới 0.
a) Khi biến x dần tới dương vô cực thì \(f\left( x \right)\) dần tới 0.
b) Khi biến x dần tới âm vô cực thì \(f\left( x \right)\) dần tới 0.
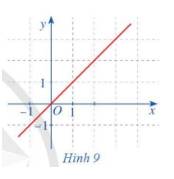
Cho hàm số \(f\left( x \right) = x\) có đồ thị như ở Hình 9. Quan sát đồ thị đó và cho biết:
a) Khi biến x dần tới dương vô cực thì \(f\left( x \right)\) dần tới đâu.
b) Khi biến x dần tới âm vô cực thì \(f\left( x \right)\) dần đâu.
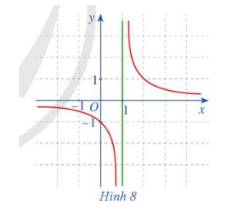
Cho hàm số \(f\left( x \right) = \frac{1}{{x - 1}}\,\,\left( {x \ne 1} \right)\) có đồ thị như ở Hình 8. Quan sát đồ thị đó và cho biết:
a) Khi biến x dần tới 1 về bên phải thì \(f\left( x \right)\) dần tới đâu.
b) Khi biến x dần tới 1 về bên trái thì \(f\left( x \right)\) dần tới đâu.
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l} - 1,\,\,x < 0\\0,\,\,x = 0\\1,\,\,x > 0\end{array} \right.\)
Hàm số \(f\left( x \right)\) có đồ thị ở Hình 6.
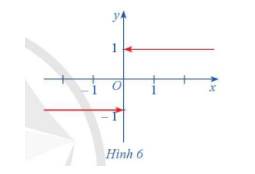
a) Xét dãy số \(\left( {{u_n}} \right)\) sao cho \({u_n} < 0\) và \(\lim {u_n} = 0.\) Xác định \(f\left( {{u_n}} \right)\) và tìm \(\lim f\left( {{u_n}} \right).\)
b) Xét dãy số \(\left( {{v_n}} \right)\) sao cho \({v_n} > 0\) và \(\lim {v_n} = 0.\) Xác định \(f\left( {{v_n}} \right)\) và tìm \(\lim f\left( {{v_n}} \right).\)
Cho hai hàm số \(f\left( x \right) = {x^2} - 1,g\left( x \right) = x + 1.\)
a) Tính \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\) và \(\mathop {\lim }\limits_{x \to 1} g\left( x \right).\)
b) Tính \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right]\)và so sánh \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right).\)
c) Tính \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) - g\left( x \right)} \right]\)và so sánh \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) - \mathop {\lim }\limits_{x \to 1} g\left( x \right).\)
d) Tính \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right).g\left( x \right)} \right]\)và so sánh \(\mathop {\lim }\limits_{x \to 1} f\left( x \right).\mathop {\lim }\limits_{x \to 1} g\left( x \right).\)
e) Tính \(\mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right)}}{{g\left( x \right)}}\)và so sánh \(\frac{{\mathop {\lim }\limits_{x \to 1} f\left( x \right)}}{{\mathop {\lim }\limits_{x \to 1} g\left( x \right)}}.\)
Biết rằng hàm số \(f\left( x \right)\) thỏa mãn \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = 3\) và \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = 5.\) Trong trường hợp này có tồn tại giới hạn \(\mathop {\lim }\limits_{x \to 2} f\left( x \right)\) hay không? Giải thích.
Xét hàm số \(f\left( x \right) = 2x.\)
a) Xét dãy số \(\left( {{x_n}} \right),\) với \({x_n} = 1 + \frac{1}{n}.\) Hoàn thành bảng giá trị \(f\left( {{x_n}} \right)\) tương ứng.

Các giá trị tương ứng của hàm số \(f\left( {{x_1}} \right),f\left( {{x_2}} \right),...,f\left( {{x_n}} \right),...\) lập thành một dãy số mà ta kí hiệu là \(\left( {f\left( {{x_n}} \right)} \right).\) Tìm \(\lim f\left( {{x_n}} \right).\)
b) Chứng minh rằng với dãy số bất kì \(\left( {{x_n}} \right),{x_n} \to 1\) ta luôn có \(f\left( {{x_n}} \right) \to 2.\)
Tính:
a) \(\mathop {\lim }\limits_{x \to 2} \left[ {\left( {x + 1} \right)\left( {{x^2} + 2x} \right)} \right];\)
b) \(\mathop {\lim }\limits_{x \to 2} \sqrt {{x^2} + x + 3} .\)
Tính các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to 2} \left( {{x^2} - 4x + 3} \right);\)
b) \(\mathop {\lim }\limits_{x \to 3} \frac{{{x^2} - 5x + 6}}{{x - 3}};\)
c) \(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt x - 1}}{{x - 1}}.\)
Tính \(\mathop {\lim }\limits_{x \to - {4^ + }} \left( {\sqrt {x + 4} + x} \right)\)