Cho tam giác ABC đường cao AH. Biết AB=6cm, AC=8cm
Viết tỉ số khối lượng của góc B và C
1, Cho tam giác ABC vuông tại A. Biết AB = 7cm và AC = 21cm. Tính các tỉ số lượng giác của góc B và góc C
2, Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5xm
a) Chứng minh tam giác ABC vuông tại A
b) Tính góc B, C vào đường cao AH của tam giác
c) Tính diện tích của tam giác ABC
cho tam giác ABC vuông tại A .Biết AB=7cm và AC=21 cm .tính các tỉ số lượng giác của góc B vá góc C
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu của H trên AB, AC. a) Viết tỉ số lượng giác góc B của AABC. b) Cho AB=6cm, AC = 8cm . Tính BC,AH c ) Chứng minh: AE.AB = AF AC
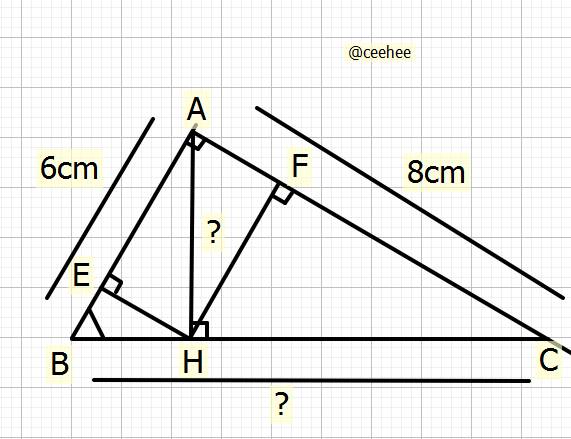
`a)` Tỉ số lượng giác góc `B` của \(\Delta ABC\)
\(SinB=\dfrac{AC}{BC}\\ CosB=\dfrac{AB}{BC}\\ TanB=\dfrac{AC}{AB}\\ CotB=\dfrac{AB}{AC}\)
`b)` Tính `BC,AH`
Xét \(\Delta ABC\) vuông tại `A`, đường cao `AH`
Ta có: \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\left(htl\right)\)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{6^2}+\dfrac{1}{8^2}\\ \Rightarrow\dfrac{1}{AH^2}=\dfrac{25}{576}\\ \Rightarrow AH^2=\dfrac{576\cdot1}{25}=23,04\\ \Rightarrow AH=\sqrt{23,04}=4,8cm\)
Ta có: \(AB\cdot AC=AH\cdot BC\left(htl\right)\)
\(\Rightarrow6\cdot8=4,8\cdot BC\\ \Rightarrow48=4,8\cdot BC\\ \Rightarrow BC=\dfrac{48}{4,8}\\ \Rightarrow BC=10cm\)
Vậy: `AH = 4,8cm; BC= 10cm`
`c)` C/m: `AE * AB = AF * AC`
Xét \(\Delta AHB\) vuông tại `H`, đường cao `HE`
Ta có: \(AH^2=AE\cdot AB\left(htl\right)\) `(1)`
Xét \(\Delta AHC\) vuông tại `H`, đường cao `HF`
Ta có: \(AH^2=AF\cdot AC\left(htl\right)\) `(2)`
Từ `(1)` và `(2)` \(\Rightarrow AH^2=AH^2\)
\(\Rightarrow AE\cdot AB=AF\cdot AC\left(=AH^2\right).\)
Cho tam giác ABC vuông tại A, đường cao AH. Tia phân giác của góc ABC cắt AH ở D và cắt AC ở E.
a) Chứng minh : AB.HD = AE.HB
b) Tính tỉ số diện tích của hai tam giác ABE và BHD biết AB = 6cm và AC = 8cm.
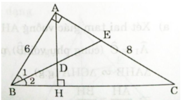
a) Ta có BE là phân giác của ∠ABC (gt)
⇒ ∠B1 = ∠B2
Do đó hai tam giác vuông:
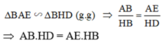
b) Ta có:
![]()
(định lý Pitago)
Xét hai tam giác vuông AHB và CAB có góc B chung nên :
![]()
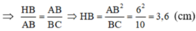
![]()

Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 3cm; BC = 5cm. a/ Tính AC, AH, HB, HC. b/ Tính các tỉ số lượng giác của góc B và tính góc C. c/ Vẽ HM vuông góc AB tại M; vẽ HN vuông góc AC tại N. Chứng minh: AM. AB = AN. AC.
c: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
giúp mk câu c) thôi đc ko ạ:(
Cho tam giác ABC vuông tại A, có đường cao AH. Biết AB= 6cm, AC= 8cm
a) Chứng minh tam giác HBA đồng dạng với tam giác ABC
b) Tính độ dài BC và AH
c) Phân giác của góc ABC cắt AH tại E, cắt AB tại D. Tính tỉ số diện tích của 2 tam giác ACD và HCE
đường cao AH. AB=6cm AC=8cm a) chứng minh tam giác HAC đồng dạng tam giác ABC b) Tính BC, AH c) Vẻ AD là đường phân giác của góc BAC d) Tính tỉ số diện tích tam giác HAC và tam giác HAB
a) Xét \(\Delta HAC\) và \(\Delta ABC\) có:
\(\widehat{AHC}=\widehat{BAC}=90^0\)
\(\widehat{C}\) CHUNG
suy ra: \(\Delta HAC~\Delta ABC\)
b) Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow\) \(BC^2=6^2+8^2=100\)
\(\Leftrightarrow\)\(BC=\sqrt{100}=10\)
\(\Delta HAC~\Delta ABC\) \(\Rightarrow\)\(\frac{AH}{AB}=\frac{AC}{BC}\)
hay \(\frac{AH}{6}=\frac{8}{10}\) \(\Rightarrow\) \(AH=\frac{6.8}{10}=4,8\)
mik làm dc câu a vs b giống bạn à 2 câu khi kh biết làm
cho tam giác abc,góc a =90°,đường cao ah,ab=15cm,ah=12cm.tính tỉ số lượng giác của góc b và góc c
cho tam giác ABC (A=90 độ),AB=6cm, AC=8cm vẽ đường cao AH đường phân giác BD của góc B cắt AH tại I. (D thuộc AC)
a.cm tam giác HAC đồng dạng với tam giác ABC
b.tính BC và HC
c.cm AB.BI=BD.HB
d.tính tỉ số diện tích của 2 tam giác HAC và HBA
Cho tam giác ABC vuông tại A có đường cao AH. Biết rằng: AB=6cm, AC=8cm
a)Tính BC và AH
b)Tính các tỉ số lượng giác tanB và cotC
c)Gọi M là trung điểm của AC. Tinh MHC(làm tròn đến phút)