Tìm Max Min của các biểu thức sau:
C= -4x2 +9x+7
D=-3x2-7x+12
Phân tích đa thức thành nhân tử
a) 3x2 – 9x
b) 4x2 + 7y – 4xy – 7x
Lời giải:
a. $3x^2-9x=3x(x-3)$
b. $4x^2+7y-4xy-7x=(4x^2-4xy)-(7x-7y)=4x(x-y)-7(x-y)=(x-y)(4x-7)$
Tìm đa thức A biết ( 4 x 2 - 7 x + 1 ) - A = ( 3 x 2 - 7 x - 1 )
A. 7 x 2 + 2
B. x 2 - 14 x + 2
C. x 2 + 2
D. x 2 - 2
Ta có: A = (4x2 - 7x + 1) - (3x2 - 7x - 1) = x2 + 2. Chọn C
cho 2 số x, y thỏa mãn: 2x2 + 7x + 7y +2xy + y2 + 12 =0
Tìm min, max của biểu thức P= x+ y+ 2
\(2x^2+7x+7y+2xy+y^2+12=0\)
\(\Leftrightarrow\left(x^2+y^2+4+2\left(xy+2x+2y\right)\right)+3\left(x+y+2\right)+2=-x^2\)
\(\Leftrightarrow\left(x+y+2\right)^2+3\left(x+y+2\right)+2=-x^2\)
\(\Leftrightarrow P^2+3P+2=-x^2\le0\)
\(\Leftrightarrow-2\le P\le-1\)
Tìm hệ số của mỗi đa thức sau
a) f (x) = 3x2 + 5x3 - 7x - 9
b) g(x) = 8x2 + 8 - 2x3 - 3x2 - 9x + 2x3 - 5
a) f (x) = 3x2 + 5x3 - 7x - 9
Hệ số cao nhất là: 5
Hệ số tự do là: 9
b) g(x) = 8x2 + 8 - 2x3 - 3x2 - 9x + 2x3 - 5
g(x) = ( 8x2 - 3x2) + ( 8-5) + ( -2x3 + 2x3) -9x
g(x) = 5x2 + 3 -9x
Hệ số cao nhất là: 5
Hệ số tự do là: 3
a) f (x) = 3x2 + 5x3 - 7x - 9
Hệ số cao nhất là: 5
Hệ số tự do là: 9
b) g(x) = 8x2 + 8 - 2x3 - 3x2 - 9x + 2x3 - 5
g(x) = ( 8x2 - 3x2) + ( 8-5) + ( -2x3 + 2x3) -9x
g(x) = 5x2 + 3 -9x
Hệ số cao nhất là: 5
Hệ số tự do là: 3
Dùng định nghĩa hai phân thức bằng nhau, hãy tìm đa thức A trong mỗi đẳng thức sau:
4 x 2 - 7 x + 3 x 2 - 1 = A x 2 + 2 x + 1
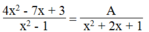 ⇒
4
x
2
-
7
x
+
3
x
2
+
2
x
+
1
=
A
x
2
-
1
⇒
4
x
2
-
7
x
+
3
x
2
+
2
x
+
1
=
A
x
2
-
1
⇒ 4 x 2 - 4 x - 3 x + 3 x + 1 2 = A x + 1 x - 1
⇒ 4 x x - 1 - 3 x - 1 . x + 1 2 = A . x + 1 x - 1
⇒ x - 1 4 x - 3 x + 1 2 = A x + 1 x - 1
⇒ A = 4 x - 3 x + 1 = 4 x 2 + 4 x - 3 x - 3 = 4 x 2 + x - 3
Vậy 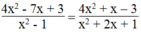
Bài 1: Tính Min hoặc Max của các biểu thức sau
A=x2-5x+8(Min)
B=6+9x2-1(min)
C=8-10x-4x2(max)
D=9-4x2-16x4(max)
\(A_{min}=8-\frac{25}{4}\) khi x=5/2
Bmin=xem lại đề đúng như đề Bmin=5 khi x=0
C=8+25-(2x+5)^2
Cmax=8+25 khi x=-5/2
Dmax=9 khi x=0