Cho tứ giác ABCD có góc CAD= góc CBD= 90 độ. Chứng minh rằng góc ACD= góc ABD.

Những câu hỏi liên quan
Cho tứ giác ABCD có góc BAC= 25 độ góc CAD = 75 độ góc ABD = 40 độ góc CBD = 85 độ . tính số đo góc BCD?
Help me
1. Cho tứ giác ABCD có góc B 120 độ, góc C 50 độ, góc D 90 độ. Tính góc A và góc ngoài của góc A2. chó tứ giác ABCD biết chu vi tam giác ABD 68cm, tam giácBCD 40cm,chu vi tứ giác ABCD 54cm. Tính độ dài đường chéo BD3. Chứng minh rằng các góc của 1 tứ giác không thể đều là góc nhọn, không đều là góc tù 4. Cho tứ giác ABCD có AB BC, BDCA a) Chứng minh BD là đường trung trực của AC b) góc B 120 độ, góc D 80 độ.Tính góc A, góc C
Đọc tiếp
1. Cho tứ giác ABCD có góc B= 120 độ, góc C= 50 độ, góc D= 90 độ. Tính góc A và góc ngoài của góc A
2. chó tứ giác ABCD biết chu vi tam giác ABD= 68cm, tam giácBCD= 40cm,chu vi tứ giác ABCD= 54cm. Tính độ dài đường chéo BD
3. Chứng minh rằng các góc của 1 tứ giác không thể đều là góc nhọn, không đều là góc tù
4. Cho tứ giác ABCD có AB= BC, BD=CA
a) Chứng minh BD là đường trung trực của AC
b) góc B= 120 độ, góc D= 80 độ.Tính góc A, góc C
4: Sửa đề: DA=DC
a: BA=BC
DA=DC
=>BD là trung trực của AC
b: góc A+góc C=360-120-80=160 độ
Xét ΔBAD và ΔBCD có
BA=BD
AD=CD
BD chung
=>ΔBAD=ΔBCD
=>góc BAD=góc BCD=160/2=80 độ
3: Nếu bốn góc trong tứ giác đều là góc nhọn thì chắc chắn tổng 4 góc cộng lại sẽ nhỏ hơn 360 độ
=>Trái với định lí tổng 4 góc trong một tứ giác
Nếu bốn góc trong tứ giác đều là góc tù thì chắc chắn tổng 4 góc cộng lại sẽ lớn hơn 360 độ
=>Trái với định lí tổng 4 góc trong một tứ giác
Do đó: 4 góc trong 1 tứ giác không thể đều là góc nhọn hay đều là góc tù được
Đúng 0
Bình luận (0)
Cho tam giác cân ABC (AB = AC). Trên tia đối của tia CA lấy một điểm D nào đó:
a) Chứng minh rằng: Góc ABD = ( Góc CBD + Góc CBD ) + Góc CDB.
b) Cho góc A = 30 độ và góc ABD = 90 độ. Tìm góc CBD.
cho tứ giác ABCD có: góc DAC = góc DBC = 90 độ. cmr:
a) góc ADB = góc ACB
b) góc ABD = góc ACD
Cho tứ giác ABCD có góc ABD=ACD=90 độ. Tính độ dài đoạn thẳng CD, biết rằng AB=BC=2cm và AD=8cm
Cho tứ giác ABCD, biết rằng AB=AD, góc B=90 độ, góc A=60 độ, góc D=135 độ
a) Tính góc C
b) Chứng minh rằng tam giác ABD đều, từ ccos chúng minh AB=AC
c) Từ góc A, kẻ AE vuông góc với đường thẳng CD, (E thuộc CD). Tính các góc của tam giác AEC
giúp em với ạ, em cảm ơn
a: góc C=360-90-60-135=210-135=75 độ
b: Xét ΔABD có AB=AD và góc BAD=60 độ
nên ΔABD đều
Đúng 0
Bình luận (0)
Cho 2 tam giác ABC và ABD có AB = AC = CA = 3cm, AD = BD = 2cm ( C và D nằm khác phía đối với AB ). Chứng minh rằng: góc CAD = góc CBD.
Xét tam giác ABC và tam giác ABD, có:
AC=CD ( gt )
CD là cạnh chung
AD=BD ( gt )
Vậy CAD=CBD (c.c.c )
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có góc BCD = góc BDC = 50 độ, góc ACD = góc ADB = 30 độ. Gọi I là giao điểm của AC và BD. Chứng minh rằng tam giác ABI cân.
góc DIC=180-50-30=100 độ
=>góc AIB=100 độ
góc IAD=180-80-30=70 độ
góc IBC=100-20=80 độ
Đến đây mình thua rồi, xin lỗi bạn nhiều nha, nhưng hình như đề này chưa đủ dữ kiện để cm ΔABI cân đâu ạ
Đúng 1
Bình luận (1)
Cho tứ diện ABCD có \(\widehat {CBD} = {90^0}.\)
a) Gọi M, N tương ứng là trung điểm của AB, AD. Chứng minh rằng MN vuông góc
BC.
b) Gọi G, K tương ứng là trọng tâm của các tam giác ABC, ACD. Chứng minh rằng
GK vuông góc với BC.
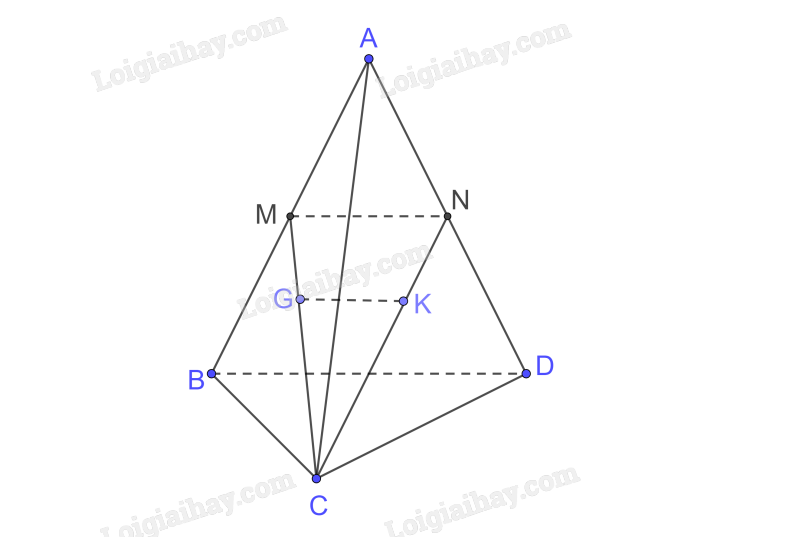
a) Xét tam giác ABD có
M, N tương ứng là trung điểm của AB, AD
\( \Rightarrow \) MN là đường trung bình của tam giác ABD
\( \Rightarrow \) MN // BD mà BD \( \bot \) BC (\(\widehat {CBD} = {90^0}\))
\( \Rightarrow \) MN \( \bot \) BC.
b) Vì G, K tương ứng là trọng tâm của các tam giác ABC, ACD nên \(\frac{{CG}}{{CM}} = \frac{{CK}}{{CN}} = \frac{2}{3}\)
\( \Rightarrow \) GK // MN (Định lý Talet) mà MN \( \bot \) BC
\( \Rightarrow \) GK \( \bot \) BC.
Đúng 0
Bình luận (0)














