Tìm tất cả các số nguyê n để:
Phân số P= \(\frac{10x+25}{2x+4}\)đạt giá trị nhỏ nhất
Tìm tất cả các số nguyên n để:
Phân số \(\dfrac{n+1}{n-2}\) có giá trị là một sô nguyên
`(n+1)/(n-2)`
Ta có:
`(n+1)/(n-2)`
`=> (n -2+3)/(n-2)`
`=> 3/(n-2)` hay `n-2 in Ư(3)`
Ta có: `Ư(3)={1;-1;3;-3}`
`=> n in {3;1;5;-1}`
Vậy: `n in {3;1;5;-1}`
Để A nguyên thì n-2+3 chia hết cho n-2
=>\(n-2\in\left\{1;-1;3;-3\right\}\)
=>\(n\in\left\{3;1;5;-1\right\}\)
Tìm x thuộc số nguyên sao cho biểu thức A = \(\dfrac{10x+25}{2x+4}\) đạt giá trị nhỏ nhất.
Do `x ∈ Z => 2x` là só chẵn `=> 2x + 4` là số chẵn
`A = (10x + 25)/(2x+4)`
`= (10x + 20)/(2x+4) + 5/(2x+4)`
`= 5 + 5/(2x+4)`
`A ` có giá trị nhỏ nhất khi `5/(2x+4)` có giá trị nhỏ nhất
`<=> 2x+4` là số nguyên âm nhỏ nhất
`<=> 2x + 4 = -2`
`<=> 2x = -6`
`<=> x = -3`
Vậy `A ` đạt giá trị nhỏ nhất `<=> x = -3`
tìm giá trị nhỏ nhất của phân số D=\(\frac{10x+25}{2x+4}\)
Tìm tất cả các số nguyên x sao cho biểu thức \(A=\frac{2019}{\left|2x-6\right|-4}\) đạt giá trị nhỏ nhất.
Giải thích chi tiết dùm mình nhé!
Vì \(\left|2x-6\right|\ge0\forall x;\left|2x-6\right|-4\ge-4\)
\(\Rightarrow\frac{1}{\left|2x-6\right|-4}\le\frac{1}{-4}\Rightarrow\frac{2019}{\left|2x-6\right|-4}\ge\frac{2019}{-4}\Rightarrow A\ge\frac{2019}{-4}\)
Dấu ''='' xảy ra <=> x = 3
Vậy GTNN A là -2019/4 <=> x = 3
tìm tất cả các số nguyên x sao cho A= 2019/ l 2x-6l-4 đạt giá trị nhỏ nhất
nêu cách giải nữa nha
Tìm x để phân thức sau đạt giá trị nhỏ nhất
\(\frac{2x^3-5x^2+10x-4}{2x-1}\)
Lấy 2x3 - 5x2 + 10x - 4 chia cho 2x - 1 ta được x2 - 2x + 4
Phân tích x2 - 2x + 4 = x2 -2x + 1 + 3 = (x + 1)2 + 3 ==> x = -1 đề có GTNN = 3
Tìm tất cả các số nguyên x để các phân số sau có giá trị là số nguyên: C=\(\frac{10x-9}{2x-3}\)
Để C nguyên thì : 10x - 9 chia hết cho 2x - 3
<=> 10x - 15 + 6 chia hết cho 2x - 3
<=> 5(2x - 3) + 6 chia hết cho 2x - 3
=> 6 chia hết cho 2x - 3
=> 2x - 3 thuộc Ư(6) = {-6;-3;-2;-1;1;2;3;6}
Ta có bảng :
| 2x - 3 | -6 | -3 | -2 | -1 | 1 | 2 | 3 | 6 |
| 2x | -3 | 0 | 1 | 2 | 4 | 5 | 6 | 9 |
| x | 0 | 1 | 2 | 3 |
Tìm tất cả các giá trị thực của tham số m để hàm số 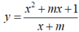 liên tục và đạt giá trị nhỏ nhất trên [0;2] tại một điểm
x
0
∈
(
0
;
2
)
.
liên tục và đạt giá trị nhỏ nhất trên [0;2] tại một điểm
x
0
∈
(
0
;
2
)
.
A. m > 1
B. -1 < m < 1
C. m > 2
D. 0 < m < 1