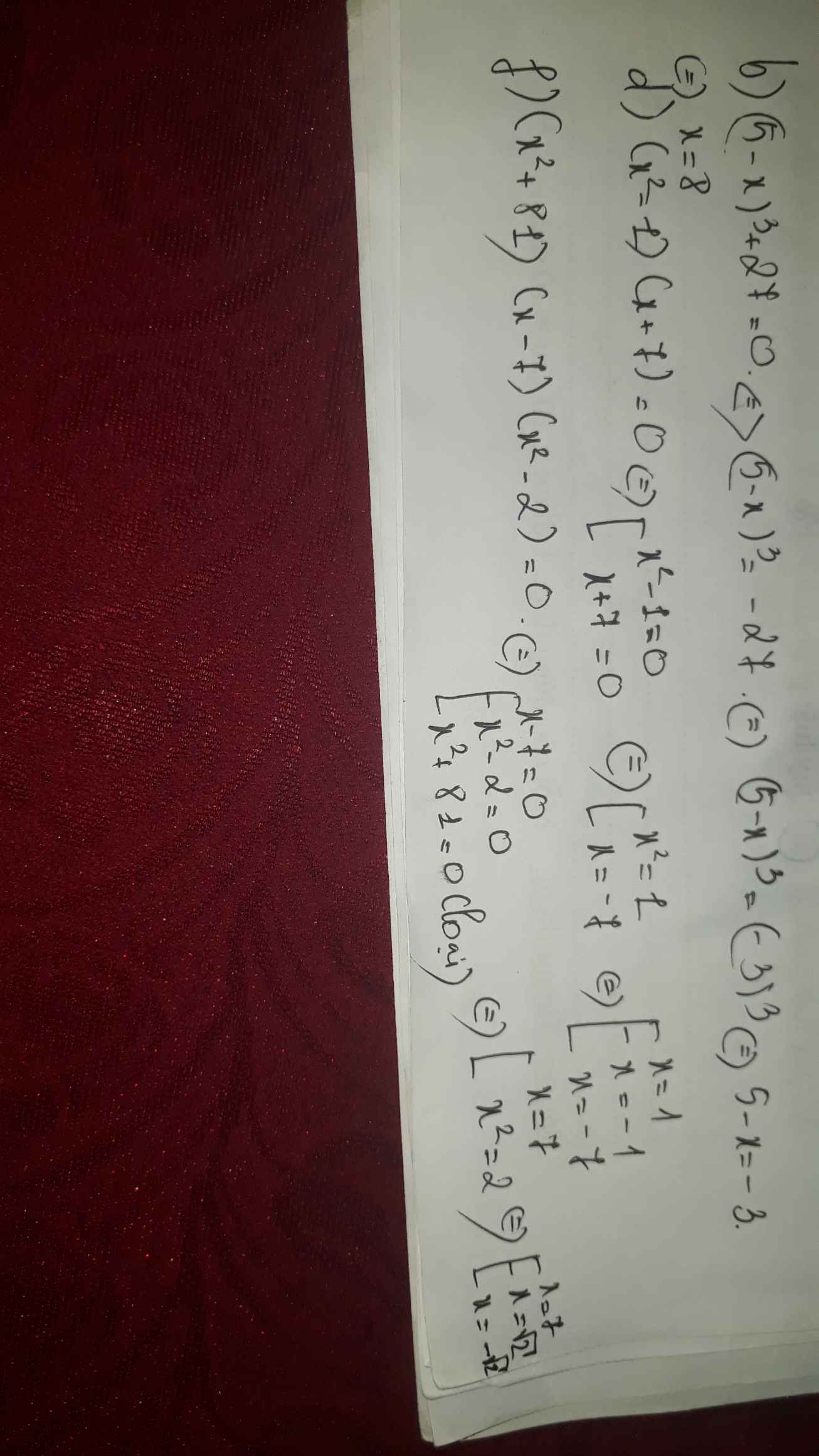1: \(\Leftrightarrow2x^2-10x-3x-2x^2=0\)

=>-13x=0

=>x=0

2: \(\Leftrightarrow5x-2x^2+2x^2-2x=13\)

=>3x=13

=>x=13/3

3: \(\Leftrightarrow4x^4-6x^3-4x^3+6x^3-2x^2=0\)

=>-2x^2=0

=>x=0

4: \(\Leftrightarrow5x^2-5x-5x^2+7x-10x+14=6\)

=>-8x=6-14=-8

=>x=1

`1)2x(x-5)-(3x+2x^2)=0`

`<=>2x^2-10x-3x-2x^2=0`

`<=>-13x=0`

`<=>x=0`

___________________________________________________

`2)x(5-2x)+2x(x-1)=13`

`<=>5x-2x^2+2x^2-2x=13`

`<=>3x=13<=>x=13/3`

___________________________________________________

`3)2x^3(2x-3)-x^2(4x^2-6x+2)=0`

`<=>4x^4-6x^3-4x^4+6x^3-2x^2=0`

`<=>x=0`

___________________________________________________

`4)5x(x-1)-(x+2)(5x-7)=0`

`<=>5x^2-5x-5x^2+7x-10x+14=0`

`<=>-8x=-14`

`<=>x=7/4`

___________________________________________________

`5)6x^2-(2x-3)(3x+2)=1`

`<=>6x^2-6x^2-4x+9x+6=1`

`<=>5x=-5<=>x=-1`

___________________________________________________

`6)2x(1-x)+5=9-2x^2`

`<=>2x-2x^2+5=9-2x^2`

`<=>2x=4<=>x=2`

len google di ban

mk chua hoc bai nay

1) Ta có: \(\left(3-x^2\right)+6-2x=0\)

\(\Leftrightarrow3-x^2+6-2x=0\)

\(\Leftrightarrow-x^2-2x+9=0\)

\(\Leftrightarrow x^2+2x-9=0\)

\(\Leftrightarrow x^2+2x+1=10\)

\(\Leftrightarrow\left(x+1\right)^2=10\)

\(\Leftrightarrow\left[{}\begin{matrix}x+1=\sqrt{10}\\x+1=-\sqrt{10}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{10}-1\\x=-\sqrt{10}-1\end{matrix}\right.\)

Vậy: \(S=\left\{\sqrt{10}-1;-\sqrt{10}-1\right\}\)

2) Ta có: \(5\left(2x-1\right)+7=4\left(2-x\right)+2\)

\(\Leftrightarrow10x-5+7=8-4x+2\)

\(\Leftrightarrow10x+4x=8+2+5-7\)

\(\Leftrightarrow14x=8\)

\(\Leftrightarrow x=\dfrac{4}{7}\)

Vậy: \(S=\left\{\dfrac{4}{7}\right\}\)

3) Ta có: \(x^2-6x+4\left(x-6\right)=0\)

\(\Leftrightarrow x\left(x-6\right)+4\left(x-6\right)=0\)

\(\Leftrightarrow\left(x-6\right)\left(x+4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-6=0\\x+4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-4\end{matrix}\right.\)

Vậy: S={6;-4}

Mk ko chép lại đề nha !

\(4x^2-4x+1+x^2+6x+9-5x^2+245=0\)

\(2x+255=0\)

\(2x=-255\)

\(x=\frac{-225}{2}\)

(2x - 1)² + (x + 3)² - 5(x + 7)(x - 7)      = 0

4x² - 4x + 1 + x² + 6x + 9 - 5x² + 245 = 0

                                             2x + 255 = 0

                                             2x           = -255

                                               x           = -127,5.

a, \(\left(x+4\right)^2-\left(x+1\right)\left(x-1\right)=16\)

\(\Leftrightarrow x^2+8x+16-\left(x^2-x+x-1\right)=16\)

\(\Leftrightarrow8x+1=0\Leftrightarrow x=-\frac{1}{8}\)

b, \(\left(2x-1\right)^2+\left(x+3\right)^2-5\left(x+7\right)\left(x-7\right)=0\)

\(\Leftrightarrow4x^2-4x+1+x^2+6x+9-5\left(x^2-49\right)=0\)

\(\Leftrightarrow2x+255=0\Leftrightarrow x=-\frac{225}{2}\)

c, \(\left(x+2\right)\left(x-2\right)-x^3-2x=15\)

\(\Leftrightarrow x^2-4-x^3-2x=15\)( vô nghiệm )

d, \(\left(x+3\right)^3-x\left(3x+1\right)^2+\left(2x+1\right)\left(4x^2-2x+1\right)=28\)

\(\Leftrightarrow x^3+9x^2+27x+27-9x^3+6x^2-x+8x^3+1=28\)

\(\Leftrightarrow15x^2+26=0\Leftrightarrow x^2\ne-\frac{26}{15}\)( vô nghiệm )

Tính nhẩm hết á, sai bỏ quá nhá, sắp đi hc ... nên chất lượng hơi kém xíu ~~~ 

a) ( x + 4 )² - ( x + 1 )( x - 1 ) = 16

<=> x² + 8x + 16 - ( x² - 1 ) = 16

<=> x² + 8x + 16 - x² + 1 = 16

<=> 8x + 17 = 16

<=> 8x = -1

<=> x = -1/8

b) ( 2x - 1 )² + ( x + 3 )² - 5( x + 7 )( x - 7 ) = 0

<=> 4x² - 4x + 1 + x² + 6x + 9 - 5( x² - 49 ) = 0

<=> 5x² + 2x + 10 - 5x² + 245 = 0

<=> 2x + 255 = 0

<=> 2x = -255

<=> 2x = -255/2

c) ( x + 2 )( x² - 2x + 4 ) - x( x² + 2 ) = 15

<=> x³ + 2³ - x³ - 2x = 15

<=> 8 - 2x = 15

<=> 2x = -7

<=> x = -7/2

d) ( x + 3 )³ - x( 3x + 1 )² + ( 2x + 1 )( 4x² - 2x + 1 ) = 28

<=> x³ + 9x² + 27x + 27 - x( 9x² + 6x + 1 ) + [ ( 2x )³ + 1³ ] = 28

<=> x³ + 9x² + 27x + 27 - 9x³ - 6x² - x + 8x³ + 1 = 28

<=> 3x² + 26x + 28 = 28

<=> 3x² + 26x = 0

<=> x( 3x + 26 ) = 0

<=> \(\orbr{\begin{cases}x=0\\3x+26=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x=-\frac{26}{3}\end{cases}}\)

a,\((x+4)^2-(x+1)(x-1)=16\)

 \(\Rightarrow x^2+8x+16-x^2+1=16\)

\(\Rightarrow 8x=-1\Rightarrow x=-\dfrac{1}{8}\)

b,\((2x-1)^2-(x+3)^2-5(x+7)(x-7)=0\)

\(\Rightarrow 4x^2-4x+1-(x^2+6x+9)-5(x^2-49)=0\)

\(\Rightarrow 4x^2-4x+1-x^2-6x-9-5x^2-245=0\)

\(\Rightarrow -x^2-10x-244=0\)

\(\Rightarrow -(x^2-10x+25)-219=0\)

\(\Rightarrow -(x-5)^2-219=0\)

\(\Rightarrow (x-5)^2+219=0\)

Mà \((x-5)^2+219>0\) suy ra PT vô nghiệm

( 2x - 1 )² + ( x + 3 )² - 5( x + 7 )( x - 7 ) = 0

<=> ( 2x - 1 )² + ( x + 3 )² - 5( x² - 7² ) = 0

<=> 4x² - 4x + 1 + x² + 6x + 9 - 5x² + 245 = 0

<=> 2x + 255 = 0

<=> 2x = -255

<=> x = -255/2

\(pt< =>4x^2-4x+1+x^2+6x+9-5x^2+5.49=0\)

\(< =>2x+255=0< =>x=-\frac{255}{2}\)

\(\left(2x-1\right)^2+\left(x+3\right)^2-5\left(x+7\right)\left(x-7\right)=0\)

\(\Leftrightarrow\left(4x^2-4x+1\right)+\left(x^2+6x+9\right)-5\left(x^2-49\right)=0\)

\(\Leftrightarrow4x^2-4x+1+x^2+6x+9-5x^2+245=0\)

\(\Leftrightarrow2x+255=0\)

\(\Leftrightarrow2x=-255\)

\(\Leftrightarrow x=\frac{-255}{2}\)

Vậy tập nghiệm của phương trình là: \(S=\left\{\frac{-255}{2}\right\}\)

b) Ta có: \(\left(5-x\right)^3+27=0\)

\(\Leftrightarrow\left(5-x\right)^3=-27\)

\(\Leftrightarrow5-x=-3\)

hay x=8

d) Ta có: \(\left(x^2-1\right)\left(x+7\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x+7\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\\x=-7\end{matrix}\right.\)

f) Ta có: \(\left(x^2+81\right)\left(x-7\right)\left(x^2-2\right)=0\)

\(\Leftrightarrow\left(x-7\right)\left(x+\sqrt{2}\right)\left(x-\sqrt{2}\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=7\\x=\sqrt{2}\\x=-\sqrt{2}\end{matrix}\right.\)

a) \(25x^2-9=0\)

\(\Leftrightarrow\left(5x\right)^2-3^2=0\)

\(\Leftrightarrow\left(5x+3\right)\left(5x-3\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}5x-3=0\\5x+3=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{3}{5}\\x=-\frac{3}{5}\end{cases}}\)

Vậy \(S=\left\{\frac{3}{5};\frac{-3}{5}\right\}\)

b) \(\left(x+4\right)^2-\left(x+1\right)\left(x-1\right)=16\)

\(\Leftrightarrow\left(x^2+8x+16\right)-\left(x^2-1\right)=16\)

\(\Leftrightarrow x^2+8x+16-x^2+1=16\)

\(\Leftrightarrow8x+17=16\)

\(\Leftrightarrow8x=-1\)

\(\Leftrightarrow x=-\frac{1}{8}\)

Vậy.........

c)\(\left(2x-1\right)^2+\left(x+3\right)^2-5\left(x+7\right)\left(x-7\right)=0\)

\(\Leftrightarrow\left(4x^2-4x+1\right)+\left(x^2+6x+9\right)-5\left(x^2-49\right)=0\)

\(\Leftrightarrow4x^2-4x+1+x^2+6x+9-5x^2+245=0\)

\(\Leftrightarrow2x=-255\)

\(\Leftrightarrow x=-127,5\)

Vậy.............

có j sai xót mong m.n bỏ qua☺

a) \(25x^2-9=0\)                      

<=> \(\left(5x\right)^2=9\)

<=> \(\left(5x\right)^2=3^2\)

<=> \(5x=3\)

<=> \(x=\frac{3}{5}\)

b) \(\left(x+4\right)^2-\left(x-1\right)\left(x+1\right)=16\)

<=> \(x^2+2.x.4+4^2-\left(x^2-1^2\right)=16\)

<=> \(x^2+8x+16-x^2+1=16\)

<=> \(\left(x^2-x^2\right)+8x+\left(16+1\right)=16\)

<=> \(8x+17=16\)

<=> \(8x=-1\)

<=> \(x=\frac{-1}{8}\)

c) \(\left(2x-1\right)^2+\left(x+3\right)^2-5\left(x+7\right)\left(x-7\right)=0\)

<=> \(\left(2x\right)^2-2.2x.1+1^2+x^2+2.x.3+3^2-5\left(x^2-7^2\right)=0\)

<=> \(4x^2-4x+1+x^2+6x+9-5x^2+5.7^2=0\)

<=> \(\left(4x^2+x^2-5x^2\right)-\left(4x-6x\right)+\left(1+9+5.7^2\right)=0\)

<=> \(2x+245=0\)

<=> \(2x=-245\)

<=> \(x=\frac{-245}{2}\)

a) \(25x^2-9=0\)

\(\Rightarrow25x^2-3^2=0\)

\(\Rightarrow\left(25x+3\right).\left(25x-3\right)=0\)

\(\Rightarrow\orbr{\begin{cases}25x+3=0\\25x-3=0\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}25x=-3\\25x=3\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}x=\frac{-3}{25}\\x=\frac{3}{25}\end{cases}}\)

b) \(\left(x+4\right)^2-\left(x+1\right)\left(x-1\right)=16\)

\(\Rightarrow\left(x+4\right)^2-\left[\left(x+1\right)^2-\left(x-1\right)^2\right]=16\)

\(\Rightarrow\left(x+4\right)^2=16\)

\(\Rightarrow\left(x+4\right)^2=4^2\)

\(\Rightarrow x+4=4\)

\(\Rightarrow x=0\)

c) \(\left(2x-1\right)^2+\left(x+3\right)^2-5\left(x+7\right)\left(x-7\right)=0\)

\(\Rightarrow\left(2x-1\right)+2\left(2x-1\right)\left(x+3\right)+\left(x+3\right)^2-5.\left(x+7\right)^2-\left(x-7\right)^2=0\)

\(\Rightarrow2\left(x+3\right)^3=0\)

\(\Rightarrow\left(x+3\right)^2=0\)

\(\Rightarrow x=3\)