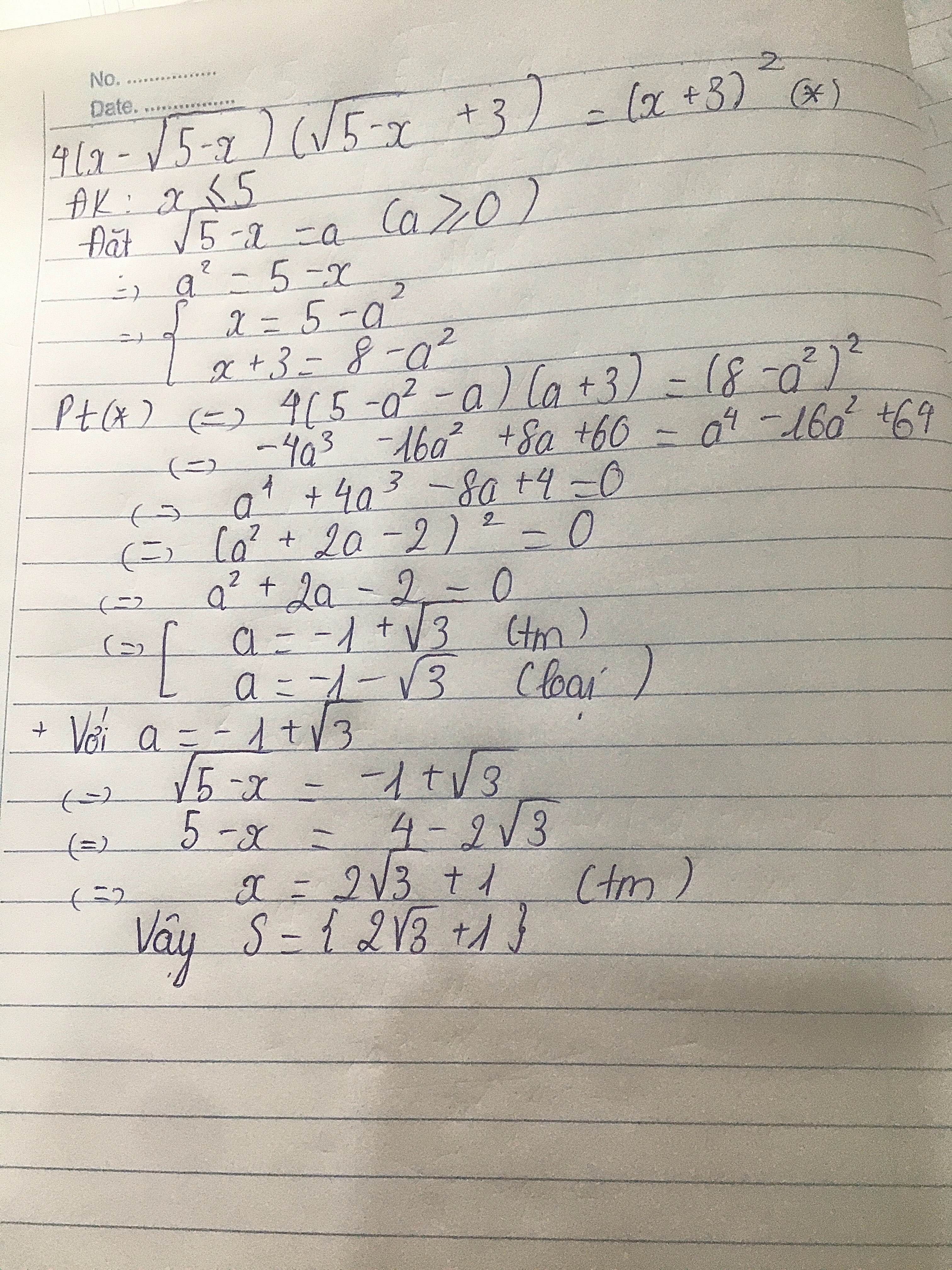tui làm bên học24 r` mà, muốn đưa link mà lỗi, thôi làm lại :(

\(pt\Leftrightarrow x^9-12x^6+48x^3-64=\left(\sqrt[3]{\left(x^2+4\right)^2}\right)^2+8\sqrt[3]{\left(x^2+4\right)^2}+16\)

\(\Leftrightarrow x^9-12x^6+48x^3-128=\left(\sqrt[3]{\left(x^2+4\right)^2}\right)^2-16+8\sqrt[3]{\left(x^2+4\right)^2}-32\)

\(\Leftrightarrow\left(x-2\right)\left(x^2+2x+4\right)\left(x^6-4x^3+16\right)=\frac{\left(x^2+4\right)^4-4096}{\left(\sqrt[3]{\left(x^2+4\right)^2}\right)^2+16}+\frac{512\left(x^2+4\right)^2-32768}{8\sqrt[3]{\left(x^2+4\right)^2}+32}\)

\(\Leftrightarrow\left(x-2\right)\left(x^2+2x+4\right)\left(x^6-4x^3+16\right)=\frac{\left(x-2\right)\left(x+2\right)\left(x^2+12\right)\left(x^4+8x^2+80\right)}{\left(\sqrt[3]{\left(x^2+4\right)^2}\right)^2+16}+\frac{512\left(x-2\right)\left(x+2\right)\left(x^2+12\right)}{8\sqrt[3]{\left(x^2+4\right)^2}+32}\)

\(\Leftrightarrow\left(x-2\right)\left(x^2+2x+4\right)\left(x^6-4x^3+16\right)-\frac{\left(x-2\right)\left(x+2\right)\left(x^2+12\right)\left(x^4+8x^2+80\right)}{\left(\sqrt[3]{\left(x^2+4\right)^2}\right)^2+16}+\frac{512\left(x-2\right)\left(x+2\right)\left(x^2+12\right)}{8\sqrt[3]{\left(x^2+4\right)^2}+32}=0\)

\(\Leftrightarrow\left(x-2\right)\left[\left(x^2+2x+4\right)\left(x^6-4x^3+16\right)-\frac{\left(x+2\right)\left(x^2+12\right)\left(x^4+8x^2+80\right)}{\left(\sqrt[3]{\left(x^2+4\right)^2}\right)^2+16}+\frac{512\left(x+2\right)\left(x^2+12\right)}{8\sqrt[3]{\left(x^2+4\right)^2}+32}\right]=0\)

Dễ thấy: pt trong ngoặc vuông vô nghiệm

\(\Rightarrow x-2=0\Rightarrow x=2\)

Đ/S :2

bài này mình chưa giải dc triệt để ở cái cuối

\(2x^3-4x^2+3x-1=2x^3\left(2-y\right)\sqrt{3-2y}\) \(\left(y\le\dfrac{3}{2}\right)\)

\(\Leftrightarrow4x^3-8x^2+6x-2=2x^3\left(4-2y\right)\sqrt{3-2y}\left(1\right)\)

\(đặt:\sqrt{3-2y}=a\ge0\Rightarrow a^2+1=4-2y\)

\(\left(1\right)\Leftrightarrow4x^3-8x^2+6x-2=2x^3.\left(a^2+1\right)a\)

\(\Leftrightarrow4x^3-8x^2+6x-2-2x^3\left(a^2+1\right)a\)

\(\Leftrightarrow-2\left(xa-x+1\right)\left[\left(xa\right)^2+x^2a+2x^2-xa-2x+1\right]=0\)

\(\Leftrightarrow x.a-x+1=0\Leftrightarrow x\left(a-1\right)=-1\Leftrightarrow x=\dfrac{-1}{a-1}\)

\(\left(\sqrt{x\sqrt{3-2y}-\sqrt{x}}\right) ^2=x\sqrt{3-2y}-\sqrt{x}\)

\(=\dfrac{-a}{a-1}-\sqrt{\dfrac{-1}{a-1}}\)

\(\left(\sqrt{x\sqrt{3-2y}+2}+\sqrt{x+1}\right)=\sqrt{\dfrac{-a}{a-1}+2}+\sqrt{\dfrac{a-2}{a-1}}\)

\(\Rightarrow\left(\dfrac{-a}{a-1}-\sqrt{-\dfrac{1}{a-1}}\right)\left(\sqrt{\dfrac{-a}{a-1}+2}+\sqrt{\dfrac{a-2}{a-1}}\right)-4=0\)

\(\Leftrightarrow\left(-\dfrac{a}{a-1}-\sqrt{-\dfrac{1}{a-1}}\right).2\sqrt{\dfrac{a-2}{a-1}}=4\)

\(\Leftrightarrow\left(-\dfrac{a}{a-1}-\sqrt{-\dfrac{1}{a-1}}\right)\sqrt{\dfrac{a-2}{a-1}}=2\)

\(\Leftrightarrow\left(-1+\dfrac{-1}{a-1}-\sqrt{-\dfrac{1}{a-1}}\right)\sqrt{1-\dfrac{1}{a-1}}=2\)(3)

\(đặt:1-\dfrac{1}{a-1}=u\Rightarrow\sqrt{-\dfrac{1}{a-1}}=\sqrt{u-1}\)

\(\left(3\right)\Leftrightarrow\left(u-2-\sqrt{u-1}\right)\sqrt{u}=2\)

bình phương lên tính được u

\(\Rightarrow u=.....\Rightarrow a\Rightarrow y=...\Rightarrow x=....\)

Với \(x=0\) không phải nghiệm

Với \(x>0\) chia 2 vế cho pt đầu cho \(x^3\)

\(\Rightarrow2-\dfrac{4}{x}+\dfrac{3}{x^2}-\dfrac{1}{x^3}=2\left(2-y\right)\sqrt{3-2y}\)

\(\Leftrightarrow1-\dfrac{1}{x}+\left(1-\dfrac{1}{x}\right)^3=\sqrt{3-2y}+\sqrt{\left(3-2y\right)^3}\)

Xét hàm \(f\left(t\right)=t+t^3\Rightarrow f'\left(t\right)=1+3t^2>0\Rightarrow f\left(t\right)\) đồng biến

\(\Rightarrow1-\dfrac{1}{x}=\sqrt{3-2y}\)

Thế vào pt dưới:

\(\left(\sqrt{x\left(1-\dfrac{1}{x}\right)-\sqrt{x}}\right)^2\left(\sqrt{x\left(1-\dfrac{1}{x}\right)+2}+\sqrt{x+1}\right)=4\)

\(\Leftrightarrow\left(x-\sqrt{x}-1\right)\left(\sqrt{x+1}+\sqrt{x+1}\right)=4\)

\(\Leftrightarrow\left(x-\sqrt{x}-1\right)\sqrt{x+1}=2\)

Phương trình này ko có nghiệm đẹp, chắc bạn ghi nhầm đề bài của pt dưới

... giải ra \(1-\dfrac{1}{x}=\sqrt{3-2y}\)

Thế xuống pt dưới:

\(\left(\sqrt{x\left(1-\dfrac{1}{x}\right)+2}\right)^2\left(\sqrt{x\left(1-\dfrac{1}{x}\right)+2}+\sqrt{x-1}\right)^4=4\)

\(\Leftrightarrow\left(x+1\right)\left(\sqrt{x+1}+\sqrt{x-1}\right)^4=4\)

Có vẻ đề bài vẫn sai

Do \(x\ge1\) theo ĐKXĐ nên \(x+1\ge2\) ; \(\left(\sqrt{x+1}+\sqrt{x-1}\right)^4\ge\left(\sqrt{2}+0\right)^4=4\)

\(\Rightarrow\left(x+1\right)\left(\sqrt{x+1}+\sqrt{x-1}\right)^4\ge8>4\) nên pt vô nghiệm

a.

Đặt \(\left\{{}\begin{matrix}\sqrt[3]{x+2}=a\\\sqrt[3]{x-2}=b\end{matrix}\right.\) ta được:

\(2a^2-b^2=ab\)

\(\Leftrightarrow\left(a-b\right)\left(2a+b\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}a=b\\2a=-b\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}a^3=b^3\\8a^3=-b^3\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x+2=x-2\left(vô-nghiệm\right)\\8\left(x+2\right)=-\left(x-2\right)\end{matrix}\right.\)

\(\Leftrightarrow x=-\dfrac{14}{9}\)

b.

Đặt \(\left\{{}\begin{matrix}\sqrt[3]{65+x}=a\\\sqrt[3]{65-x}=b\end{matrix}\right.\)

\(\Rightarrow a^2+4b^2=5ab\)

\(\Leftrightarrow\left(a-b\right)\left(a-4b\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}a=b\\a=4b\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}a^3=b^3\\a^3=64b^3\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}65+x=65-x\\65+x=64\left(65-x\right)\end{matrix}\right.\)

\(\Leftrightarrow...\)

c.

Đặt \(\left\{{}\begin{matrix}\sqrt[3]{x+2}=a\\\sqrt[3]{x+1}=b\end{matrix}\right.\)

\(\Rightarrow a+b=1+ab\)

\(\Leftrightarrow\left(a-1\right)\left(b-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}a=1\\b=1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}a^3=1\\b^3=1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x+2=1\\x+1=1\end{matrix}\right.\)

\(\Leftrightarrow...\)

Gõ đề có sai không ạ?

\(\left\{{}\begin{matrix}\sqrt{3+2x^2y-x^4y^2}+x^4\left(1-2x^2\right)=y^4\\1+\sqrt{1+\left(x-y\right)^2}=x^3\left(x^3-x+2y^2\right)\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{4-\left(1-x^2y\right)^2}=2x^6-x^4+y^4\\-\sqrt{1+\left(x-y\right)^2}=1-x^6+x^4-2x^3y^2\end{matrix}\right.\)

Cộng theo vế HPT²

\(\sqrt{4-\left(1-x^2y\right)^2}-\sqrt{1+\left(x-y\right)^2}=\left(x^3-y^2\right)^2+1\)

\(\Leftrightarrow\sqrt{4-\left(1-x^2y\right)^2}=\sqrt{1+\left(x-y\right)^2}+\left(x^3-y^2\right)^2+1\) (1)

Có:

\(\left\{{}\begin{matrix}\sqrt{4-\left(1-x^2y\right)^2}\le2\\\sqrt{1+\left(x-y\right)^2}+\left(x^2-y^2\right)^2+1\ge2\end{matrix}\right.\)

\(\Rightarrow\) (1) xảy ra \(\Leftrightarrow\) \(\left\{{}\begin{matrix}\sqrt{4-\left(1-x^2y\right)^2}=2\\\sqrt{1+\left(x-y\right)^2}=1\\\left(x^3-y^2\right)^2=0\end{matrix}\right.\Leftrightarrow x=y=1\)