Giải dùm em bài này ạ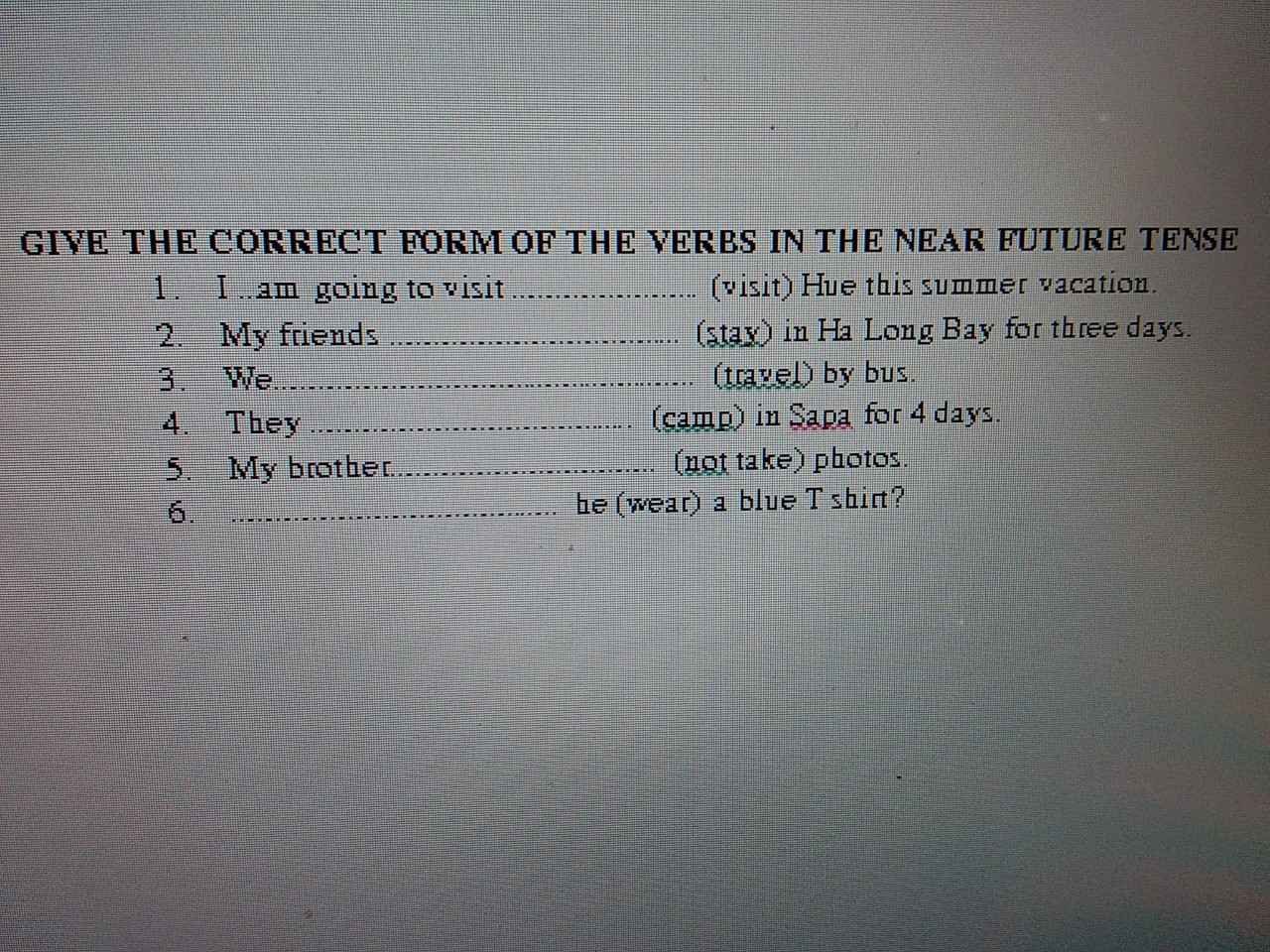

Những câu hỏi liên quan
Ai giải dùm em bài này em cảm ơn ạ!


 giải chi tiết 3 bài này dùm em vs ạ
giải chi tiết 3 bài này dùm em vs ạ
em cảm ơn mọi người nhiều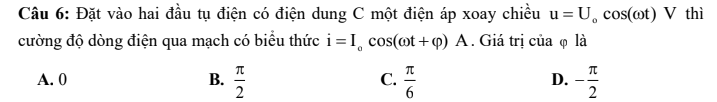
Giải dùm em bài này với ạ : (m+1)^2 >=4m
\(\left(m+1\right)^2\ge4m\Leftrightarrow m^2+2m+1\ge4m\Leftrightarrow m^2-2m+1\ge0\)\(\Leftrightarrow\left(m-1\right)^2\ge0\)
Vì \(\left(m-1\right)^2\ge0\)(luôn đúng) nên pt vô số nghiêmj
Mình cũng ko bt đây là giải pt hay cm BĐT nữa nên nếu ko đúng mục đích thì bạn thông cảm
Đúng 0
Bình luận (0)
giải dùm em mấy câu này vs ạ nãy em ghi còn thiếu
em cảm ơn mn nhiều giải thích rọ dùm em luôn vs ạ


3.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)
Đúng 3
Bình luận (1)
Câu 2 đề thiếu yêu cầu
Câu 9:
Từ đồ thị ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;0\right)\) và \(\left(2;+\infty\right)\)
\(\Rightarrow\) A đúng do \(\left(-1;0\right)\subset\left(-\infty;0\right)\)
Đúng 2
Bình luận (0)
mn giải hộ em bài toán này dùm em với ạ
5 mũ 6 :5 mũ 4 +2 mũ 3.2 mũ 2 _1 mũ 2017
= 5 mũ 2 + 2 mũ 5 - 1
= 25 + 32 -1
= 57 - 1
= 56
Đúng 0
Bình luận (0)
= 5^2 + 2 ^ 5 - 1
= 25 + 32 -1
= 57 - 1
= 56
Đúng 0
Bình luận (0)
= 5 ^ 2 + 2 ^ 5 - 1
= 25 + 32 -1
= 57 - 1
= 56
Đáp án: 56
Đúng 0
Bình luận (0)
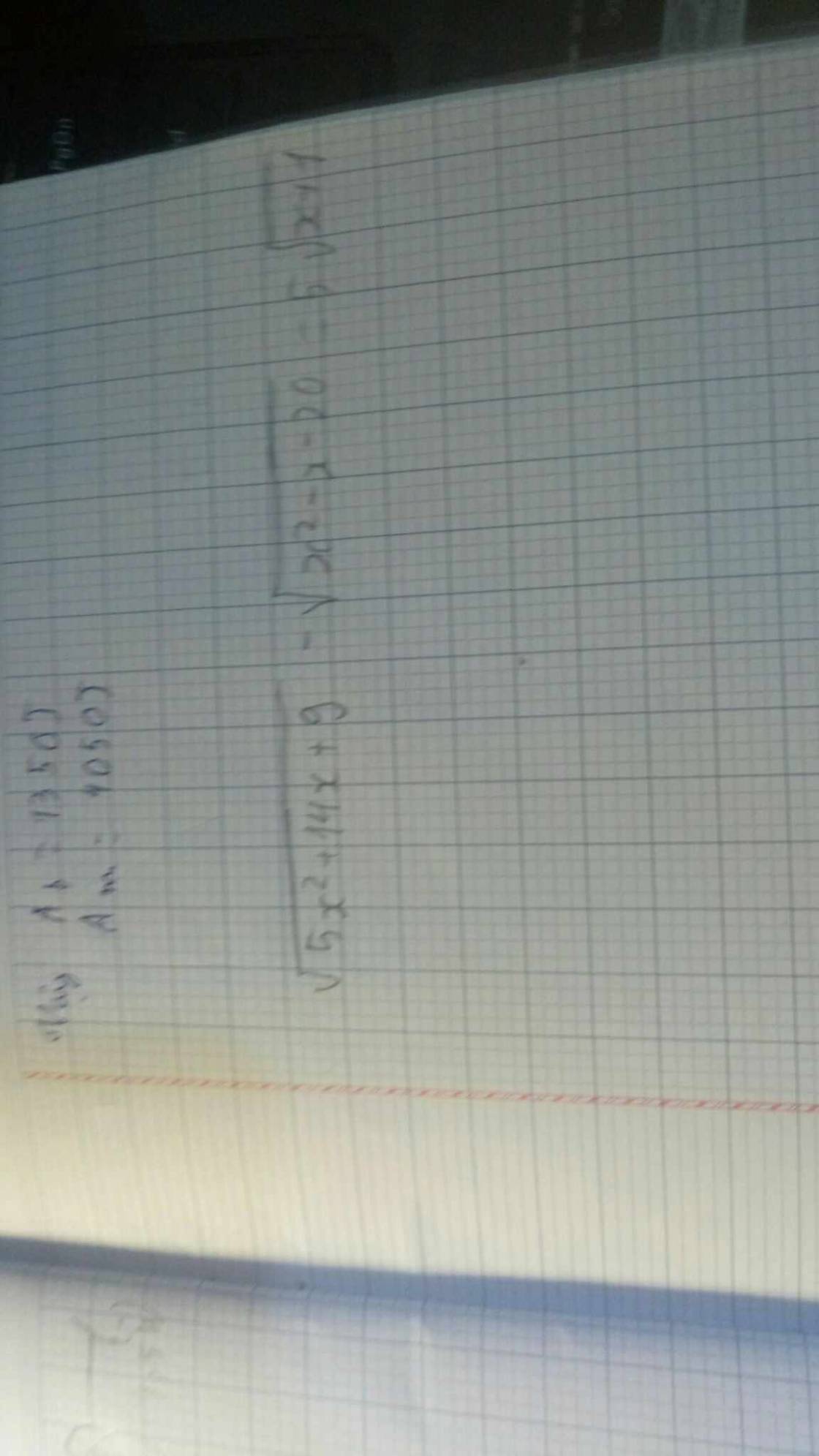 giải dùm e bài này ik ạ
giải dùm e bài này ik ạ
ĐKXĐ: \(\left\{{}\begin{matrix}5x^2+14x+9>=0\\x+1>=0\\x^2-x-20>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(x+1\right)\left(5x+9\right)>=0\\x+1>=0\\\left(x-5\right)\left(x+4\right)>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}x< =-\dfrac{9}{5}\\x>=-1\end{matrix}\right.\\x>=-1\\\left[{}\begin{matrix}x>=5\\x< =-4\end{matrix}\right.\end{matrix}\right.\)
=>x>=5
\(\sqrt{5x^2+14x+9}-\sqrt{x^2-x-20}=5\sqrt{x+1}\)
=>\(\sqrt{5x^2+14x+9}-21+6-\sqrt{x^2-x-20}=5\sqrt{x+1}-15\)
=>\(\dfrac{5x^2+14x+9-441}{\sqrt{5x^2+14x+9}+21}+\dfrac{36-x^2+x+20}{6+\sqrt{x^2-x-20}}=5\left(\sqrt{x+1}-3\right)\)
=>\(\dfrac{5x^2+14x-432}{\sqrt{5x^2+14x+9}+21}+\dfrac{-x^2+x+56}{6+\sqrt{x^2-x-20}}=5\cdot\dfrac{x+1-9}{\sqrt{x+1}+3}\)
=>\(\dfrac{\left(x-8\right)\left(5x+54\right)}{\sqrt{5x^2+14x+9}+21}-\dfrac{x^2-x-56}{\sqrt{x^2-x-20}+6}=\dfrac{5\left(x-8\right)}{\sqrt{x+1}+3}\)
=>\(\dfrac{\left(x-8\right)\left(5x+4\right)}{\sqrt{5x^2+14x+9}+21}-\dfrac{\left(x-8\right)\left(x+7\right)}{\sqrt{x^2-x-20}+6}-\dfrac{5\left(x-8\right)}{\sqrt{x+1}+3}=0\)
=>\(\left(x-8\right)\left(\dfrac{5x+4}{\sqrt{5x^2+14x+9}+21}-\dfrac{x+7}{\sqrt{x^2-x-20}+6}-\dfrac{5}{\sqrt{x+1}+3}\right)=0\)
=>x-8=0
=>x=8(nhận)
Đúng 2
Bình luận (0)
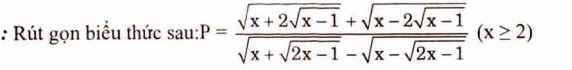 giải dùm e bài này vs ạ
giải dùm e bài này vs ạ
Lời giải:
\(P.\frac{1}{\sqrt{2}}=\frac{\sqrt{(x-1)+2\sqrt{x-1}+1}+\sqrt{(x-1)-2\sqrt{x-1}+1}}{\sqrt{(2x-1)+2\sqrt{2x-1}+1}-\sqrt{(2x-1)-2\sqrt{2x-1}+1}}\)
\(=\frac{\sqrt{(\sqrt{x-1}+1)^2}+\sqrt{(\sqrt{x-1}-1)^2}}{\sqrt{(\sqrt{2x-1}+1)^2}-\sqrt{(\sqrt{2x-1}-1)^2}}\)
\(=\frac{\sqrt{x-1}+1+\sqrt{x-1}-1}{\sqrt{2x-1}+1-(\sqrt{2x-1}-1)}=\frac{2\sqrt{x-1}}{2}=\sqrt{x-1}\)
Đúng 1
Bình luận (0)
Phân tích dùm em bài này với ạ. Em cảm ơn trước ạ

















