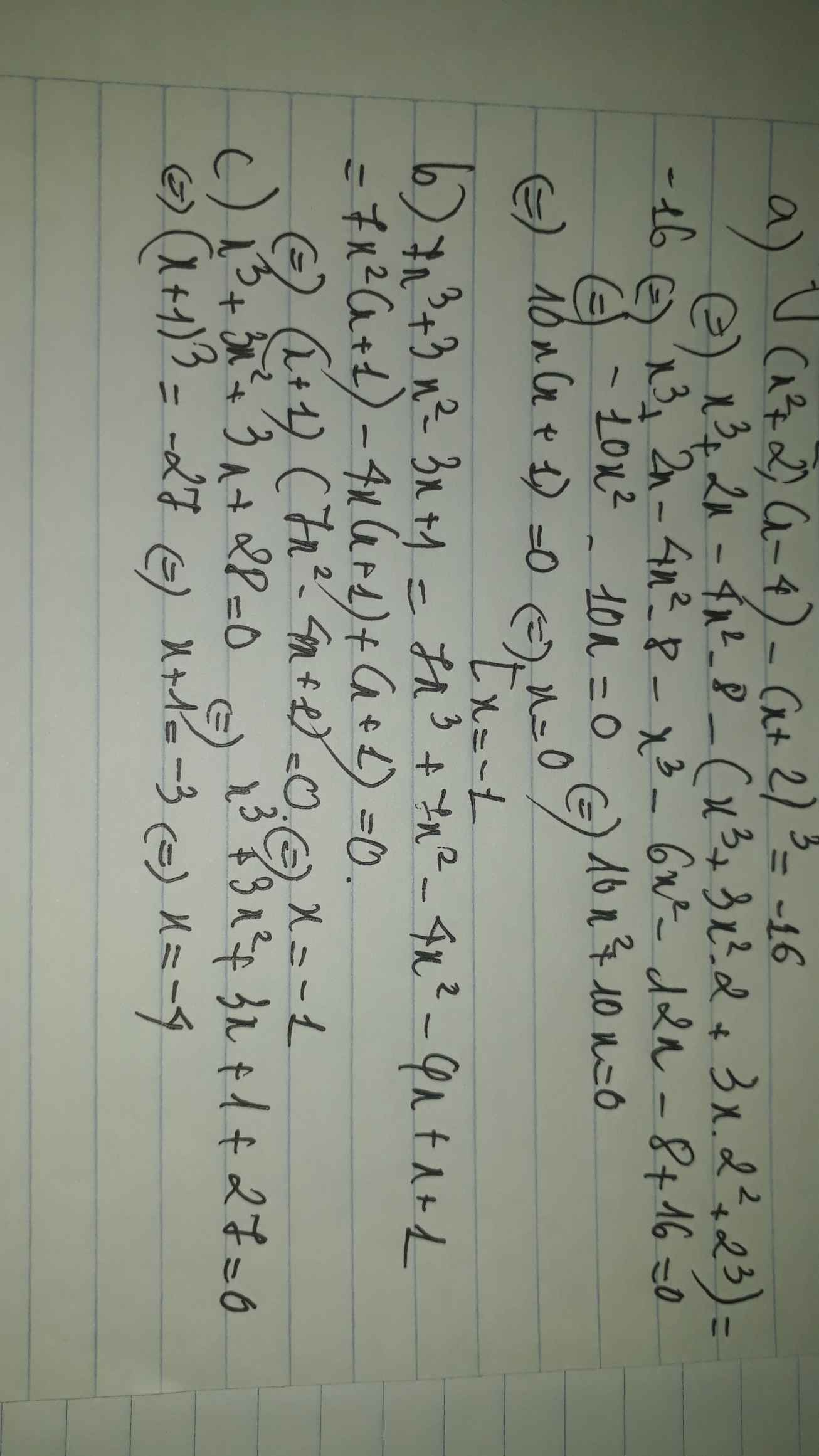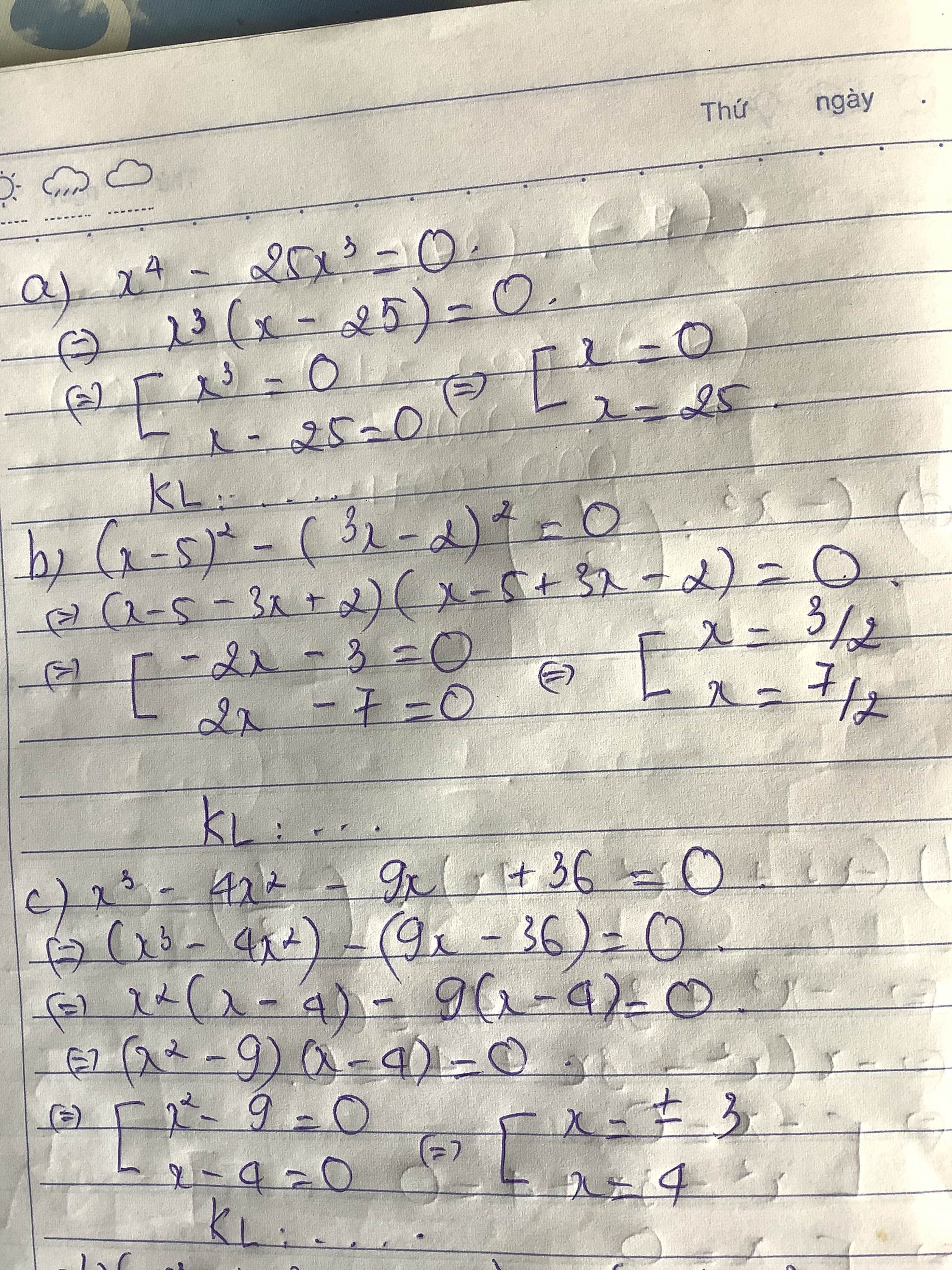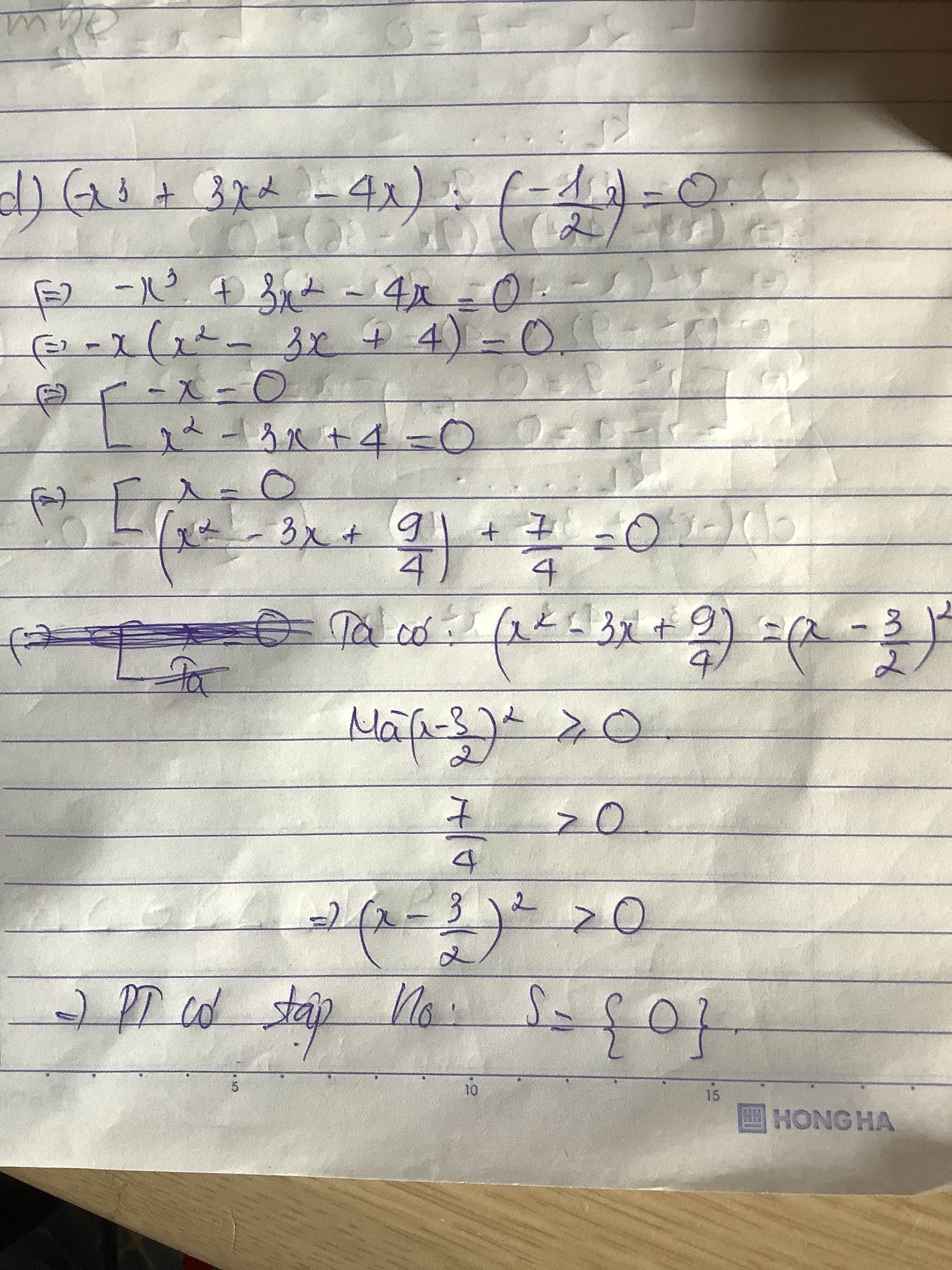\(\sqrt{2}\)x3 + 3x2 - 2 = 0

Những câu hỏi liên quan
Cho hàm số
f
(
x
)
x
3
-
3
x
2
+
2
có đồ thị là đường cong trong hình bên. Hỏi phương trình
x
3
-
3
x
2
+
2...
Đọc tiếp
Cho hàm số f ( x ) = x 3 - 3 x 2 + 2 có đồ thị là đường cong trong hình bên.
Hỏi phương trình
x
3
-
3
x
2
+
2
3
-
3
(
x
3
-
3
x
2
+
2
)
2
+
2
=
0
có bao nhiêu nghiệm thực phân biệt?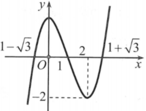
![]()
![]()
![]()
![]()
Cho hàm số
f
x
x
3
−
3
x
2
+
2
có đồ thị là đường cong trong hình bên. Hỏi phươngtrình
x
3
−
3
x
2
+
2...
Đọc tiếp
Cho hàm số
f
x
=
x
3
−
3
x
2
+
2
có đồ
thị là đường cong trong hình bên. Hỏi phương
trình
x
3
−
3
x
2
+
2
3
−
3
x
3
−
3
x
2
+
2
2
+
2
=
0
có bao nhiêu nghiệm thực phân biệt?
A. 7
B. 9
C. 6
D. 5
Cho hàm số
f
x
x
3
-
3
x
2
+
2
có đồ thị là đường cong trong hình bên.Hỏi phương trình
x
3
-
3
x
2
+
2
3...
Đọc tiếp
Cho hàm số f x = x 3 - 3 x 2 + 2 có đồ thị là đường cong trong hình bên.
Hỏi phương trình
x 3 - 3 x 2 + 2 3 - 3 x 3 - 3 x 2 + 2 2 + 2 = 0 có bao nhiêu nghiệm thực phân biệt?

A. 7.
B. 9.
C. 6.
D. 5.
Cho hàm số
f
x
x
3
−
3
x
2
+
2
có đồ thị là đường cong trong hình bên. Hỏi phương trình
x
3
−
3
x
2
+
2
3...
Đọc tiếp
Cho hàm số
f
x
=
x
3
−
3
x
2
+
2
có đồ thị là đường cong trong hình bên. Hỏi phương trình
x
3
−
3
x
2
+
2
3
−
3
x
3
−
3
x
2
+
2
2
+
2
=
0
có bao nhiêu nghiệm thực dương phân biệt? 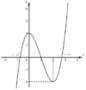
A. 3
B. 5
C. 7
D. 1
Đáp án C

Chú ý và sai lầm: Sau khi đặt ẩn phụ và tìm ra được 3 nghiệm t, nhiều học sinh kết luận sai lầm phương trình có 3 nghiệm phân biệt và chọn đáp án A. Số nghiệm của phương trình là số nghiệm x chứ không phải số nghiệm t.
Đúng 0
Bình luận (0)
Cho đồ thị hàm số
y
x
3
+
3
x
2
-
2
có các điểm cực đại A(-2;2) và điểm cực tiểu B(0;-2) thì phương trình
x
3
+
3
x
2
-
2
m
có hai nghiệm khi A.
-
2
m
2
B.
m
-
2
hoặc
m...
Đọc tiếp
Cho đồ thị hàm số y = x 3 + 3 x 2 - 2 có các điểm cực đại A(-2;2) và điểm cực tiểu B(0;-2) thì phương trình x 3 + 3 x 2 - 2 = m có hai nghiệm khi
A. - 2 < m < 2
B. m = - 2 hoặc m = 2
C. m > 2
D. m < - 2
Tìm các giới hạn
1. lim ( x đến +--∞) (x3 +3x2+2)
2. lim (x đến -∞) (\(\sqrt{4x^2-x+5}\))
3. lim ( x đến +- ∞) (\(\sqrt{x^2-2x-1}-\sqrt{x^2-7x+3}\))
1.
\(\lim\limits_{x\to +\infty}(x^3+3x^2+2)=+\infty\)
2.
\(\lim\limits_{x\to -\infty}\sqrt{4x^2-x+5}=\lim\limits_{x\to -\infty}-x.\sqrt{4+\frac{1}{x}+\frac{5}{x^2}}=+\infty\) do $-x\to +\infty$ và $\lim\limits_{x\to -\infty}\sqrt{4+\frac{1}{x}+\frac{5}{x^2}}=4>0$
Đúng 0
Bình luận (0)
3.
\(\lim\limits_{x\to +\infty}(\sqrt{x^2-2x-1}-\sqrt{x^2-7x+3})=\lim\limits_{x\to +\infty}\frac{x^2-2x-1-(x^2-7x+3)}{\sqrt{x^2-2x-1}+\sqrt{x^2-7x+3}}\)
\(=\lim\limits_{x\to +\infty}\frac{5x-4}{\sqrt{x^2-2x-1}+\sqrt{x^2-7x+3}}=\lim\limits_{x\to +\infty}\frac{5-\frac{4}{x}}{\sqrt{1-\frac{2}{x}-\frac{1}{x^2}}+\sqrt{1-\frac{7}{x}+\frac{3}{x^2}}}\)
\(=\frac{5}{1+1}=\frac{5}{2}\)
Đúng 0
Bình luận (0)
Tìm x biết:
a) x3 - 7x2 - 9x + 63 = 0
b) x3 - 3x2 + 3x - 1 + 2.(x2 - x) = 0
tìm x thỏa mãn:
a) (x2+2)(x-4)-(x+2)3=-16
b) 7x3+3x2-3x+1=0
c) x3+3x2+3x+28=0
a: Ta có: \(\left(x^2+2\right)\left(x-4\right)-\left(x+2\right)^3=-16\)
\(\Leftrightarrow x^3-4x^2+2x-8-x^3-6x^2-12x-8=-16\)
\(\Leftrightarrow-10x^2-10x=0\)
\(\Leftrightarrow-10x\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
c: Ta có: \(x^3+3x^2+3x+28=0\)
\(\Leftrightarrow\left(x+1\right)^3=-27\)
\(\Leftrightarrow x+1=-3\)
hay x=-4
Đúng 0
Bình luận (0)
Chứng minh rằng phương trình x3 -3x2-1=0 có nghiệm x thuộc (3,4) và x > 1+\(\sqrt[5]{36}\)
Em 2k8 nên e k chắc :((
Đặt f(x) = x^3 - 3x^2 - 1 = 0 => f(x) liên tục trên (3;4)
x = 3 => f(3) = -1 ; x = 4 => f(4) = 15
=> f(3) . f(4) = -15 < 0 => tồn tại no x thuộc (3;4) để f(x) = 0 ( đpcm )
Đúng 1
Bình luận (0)
Tìm x:
a) x4-25x3=0
b) (x-5)2-(3x-2)2=0
c) x3-4x2-9x+36=0
d) (-x3+3x2-4x) : (\(-\dfrac{1}{2}\)x)=0
a.
$x^4-25x^3=0$
$\Leftrightarrow x^3(x-25)=0$
\(\Leftrightarrow \left[\begin{matrix} x^3=0\\ x-25=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=0\\ x=25\end{matrix}\right.\)
b.
$(x-5)^2-(3x-2)^2=0$
$\Leftrightarrow (x-5-3x+2)(x-5+3x-2)=0$
$\Leftrightarrow (-2x-3)(4x-7)=0$
\(\Leftrightarrow \left[\begin{matrix}
-2x-3=0\\
4x-7=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix}
x=\frac{-3}{2}\\
x=\frac{7}{4}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
c.
$x^3-4x^2-9x+36=0$
$\Leftrightarrow x^2(x-4)-9(x-4)=0$
$\Leftrightarrow (x-4)(x^2-9)=0$
$\Leftrightarrow (x-4)(x-3)(x+3)=0$
\(\Leftrightarrow \left[\begin{matrix} x-4=0\\ x-3=0\\ x+3=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=4\\ x=3\\ x=-3\end{matrix}\right.\)
d. ĐK: $x\neq 0$
$(-x^3+3x^2-4x):(\frac{-1}{2}x)=0$
$\Leftrightarrow x(-x^2+3x-4):(\frac{-1}{2}x)=0$
$\Leftrightarrow -2(-x^2+3x-4)=0$
$\Leftrightarrow x^2-3x+4=0$
$\Leftrightarrow (x-1,5)^2=-1,75< 0$ (vô lý)
Vậy pt vô nghiệm.
Đúng 1
Bình luận (0)
Xem thêm câu trả lời