1:Thay x=1 và y=3 vào (d2), ta được:

\(m-2m+3=3\)

hay m=0

a, pt hoanh độ giao điểm cua 2 đg thẳng d1 và d2 la: 2x - 5 = 1 <=> x = 3

vậy tọa độ giao điểm cua d1 va d2 la A(3;1)

Để d1 , d2, d3 đồng quy thì d3 phải đi qua diem A(3;1)

Ta co pt: (2m - 3).3 - 1 = 1

<=> 6m - 9 -1 = 1

<=> 6m = 11 <=> m = 11/6

mấy bài còn lại tương tự nha

Gọi I là giao điểm của ( d 1 ) và ( d 2 ). Khi đó tọa độ của I là nghiệm của hệ phương trình: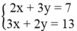 

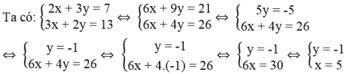
Tọa độ điểm I là I(5; -1)

Đường thẳng (d): y = (2m – 5)x – 5m đi qua I(5; -1) nên tọa độ của I nghiệm đúng phương trình đường thẳng:

Ta có: -1 = (2m – 5).5 – 5m ⇔ -1 = 10m – 25 – 5m

⇔ 5m = 24 ⇔ m = 24/5

Vậy với m = 24/5 thì đường thẳng (d) đi qua giao điểm của hai đường thẳng ( d 1 ) và ( d 2 ).

PT hoành độ giao điểm: \(3-2x=3x-2\Leftrightarrow x=1\Leftrightarrow y=1\Leftrightarrow A\left(1;1\right)\)

Để 3 đt đồng quy thì \(A\left(1;1\right)\in y=mx+m-5\)

\(\Leftrightarrow m+m-5=1\Leftrightarrow2m=6\Leftrightarrow m=3\)

Phương trình hoành độ giao điểm:

3-2x=3x-2

⇔x=1

Thay x=1 vào hàm số ➜ y=1

Vậy giao điểm hai đường thẳng y = 3 – 2x, y = 3x – 2 có tọa độ (1; 1).

Để y = mx + m – 5 qua hai đường thẳng ➜ x=1; y=1

Thay x=1; y=1 vào y = mx + m – 5

m+m-5=1

⇔m=3

Vậy m=3 để ba đường thẳng y = 3 – 2x, y = 3x – 2 và y = mx + m – 5
đồng quy tại một điểm.

Tọa độ giao điểm của hai đường thẳng (d1) và (d2) là:

\(\left\{{}\begin{matrix}2x-3y=12\\3x+4y=1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}8x-12y=48\\9x+12y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}17x=51\\3x+4y=1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=3\\4y=1-3x=1-3\cdot3=-8\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=3\\y=-2\end{matrix}\right.\)

Thay x=3 và y=-2 vào (d), ta được:

\(3\left(2m+3\right)-3m+4=-2\)

=>6m+9-3m+4=-2

=>6m+13=-2

=>6m=-15

=>\(m=-\dfrac{5}{2}\)

Đáp án D