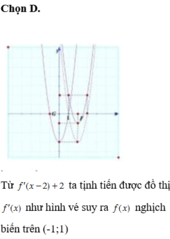
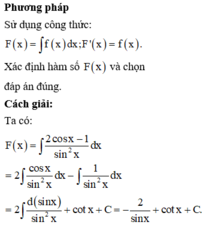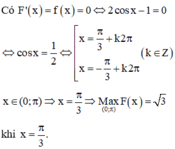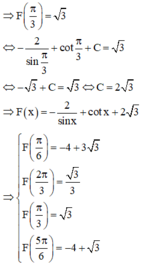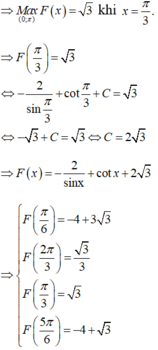Biết rằng trên khoảng (\(\frac{3}{2}\);+∞), hàm số f(x) =\(\frac{20x^2-30x+7}{\sqrt{2x-3}}\)có một hàm nguyên F(x)=(ax2+bx+c). \(\sqrt{2x-3}\), ( a,b,c∈z) . Tính S=a+b+c bằng

Những câu hỏi liên quan
CÂU 1:a)A2+2^2+...+2^{2015}+2^{2016}b) Chứng tỏ rằng A 1. Afrac{1}{2^2}+frac{1}{3^2}+frac{1}{4^2}+frac{1}{5^2}+....+frac{1}{2017^2}c)Mfrac{2}{3.5}+frac{2}{5.7}+frac{2}{7.9}+....+frac{2}{97.99}(dấu (.) là dấu nhân đó nha các bạn)d)Cfrac{1}{2.4}+frac{1}{4.6}+frac{1}{6.8}+...+frac{1}{98.100}e)CÂU 2:a)frac{-3}{2}x+frac{-1}{3}x-frac{1}{2}b)frac{-4}{3}x+frac{1}{2}-xfrac{-3}{2}-xc) frac{3}{2}:left(frac{1}{2}x+3right)-frac{4}{5}-2frac{1}{2}d)8x7,8.x+25CÂU 3:a. Trong 1 bản đồ có tỉ lệ xích là 1 : 1.000....
Đọc tiếp
CÂU 1:a)\(A=2+2^2+...+2^{2015}+2^{2016}\)
b) Chứng tỏ rằng A < 1. \(A=\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}+....+\frac{1}{2017^2}\)
c)\(M=\frac{2}{3.5}+\frac{2}{5.7}+\frac{2}{7.9}+....+\frac{2}{97.99}\)(dấu (.) là dấu nhân đó nha các bạn)
d)\(C=\frac{1}{2.4}+\frac{1}{4.6}+\frac{1}{6.8}+...+\frac{1}{98.100}\)
e)
CÂU 2:a)\(\frac{-3}{2}x+\frac{-1}{3}=x-\frac{1}{2}\)
b)\(\frac{-4}{3}x+\frac{1}{2}-x=\frac{-3}{2}-x\)
c) \(\frac{3}{2}:\left(\frac{1}{2}x+3\right)-\frac{4}{5}=-2\frac{1}{2}\)
d)\(8x=7,8.x+25\)
CÂU 3:a. Trong 1 bản đồ có tỉ lệ xích là 1 : 1.000.000, khoảng cách giữa 2 tỉnh A và B là 6,5 cm. Hỏi ở ngoài thực tế thì khoảng cách giữ 2 tỉnh đó là ?
b. Khoảng cách giữa 2 tỉnh A và B là 75km. Hỏi nếu trên bản đồ có tỉ lệ xích là 1 : 5.000.000 thì khoảng cách giữa 2 tỉnh đó là ?
c. khoảng cách giữa 2 tỉnh A và B trên ban đồ là 4,5cm. Tính khoảng cách giữa tỉnh ở ngoài thực tế biết xích đạo là 1:1,5 triệu
CÂU 4 : Tìm số tự nhiên\(a\)lớn nhất, biết rằng \(480⋮a\) và \(600⋮a\)
Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:
a) y = sinx trên khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{7\pi }}{2}} \right),\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\)
b) y = cosx trên khoảng \(\left( { - 20\pi ; - 19\pi } \right),\left( { - 9\pi ; - 8\pi } \right)\)
a) y = sinx
- Khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{7\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
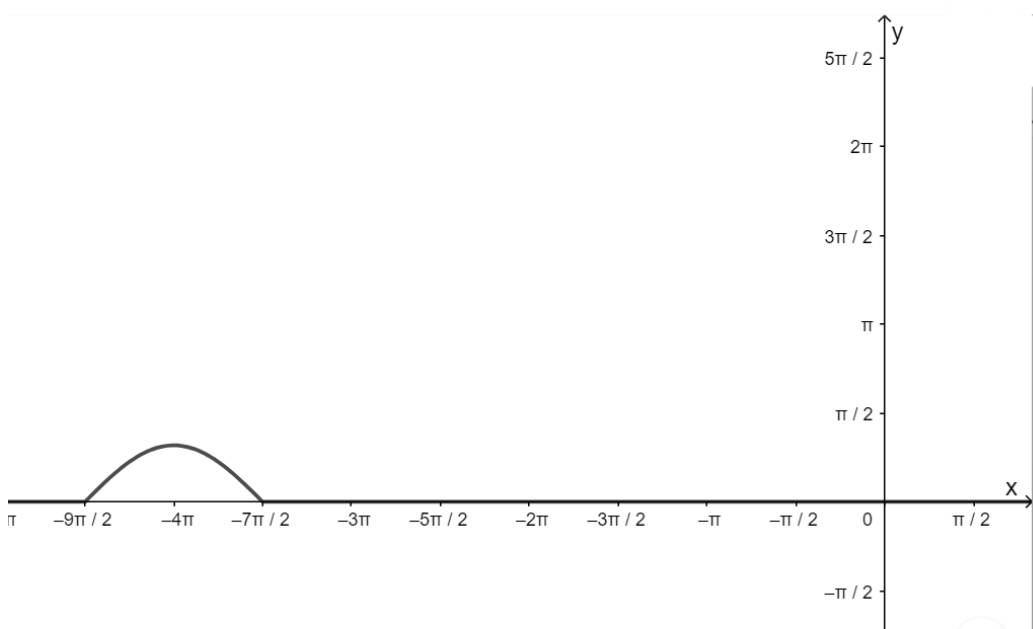
+ Đồng biến trên khoảng \(\left( { - \frac{{9\pi }}{2}; - 4\pi } \right)\)
+ Nghịch biến trên khoảng; \(\left( { - 4\pi ; - \frac{{7\pi }}{2}} \right)\)
- Khoảng \(\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
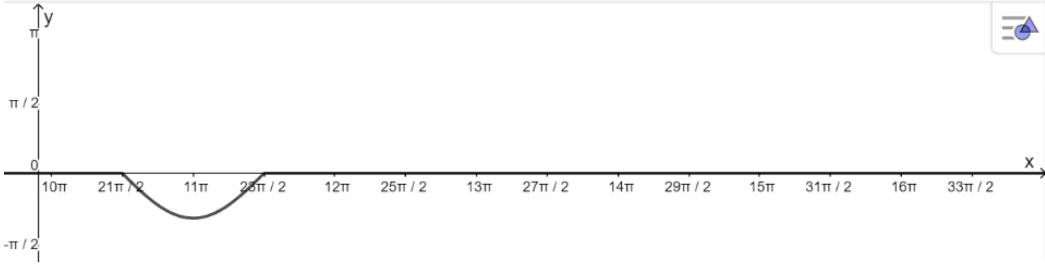
+ Đồng biến trên khoảng: \(\left( {11\pi ;\frac{{23\pi }}{2}} \right)\)
+ Nghịch biến trên khoảng: \(\left( {\frac{{21\pi }}{2};11\pi } \right)\)
Đúng 0
Bình luận (0)
a) Xác định hệ số a của paradol y = a\(x^2\), biết rằng paradol đi qua A(-2;-2)
b) Tìm tọa độ của M thuộc paradol nói trên, biết rằng khoảng cách từ M đến trục hoành gấp đôi khoảng cách từ M đến trục tung.
Biết rằng hàm số \(y = 2{x^2}{\rm{ + }}mx + n\) giảm trên khoảng \(\left( { - \infty ;1} \right),\)tăng trên khoảng \(\left( {1; + \infty } \right)\) và có tập giá trị là \([9; + \infty )\). Xác định giá trị của m và n.
Tham khảo:
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - m}}{{2.2}} = - \frac{m}{4};{y_S} = f( - \frac{m}{4})\)
Vì hàm số bậc hai có \(a = 2 > 0\) nên ta có bảng biến thiên sau:

Hàm số đạt giá trị nhỏ nhất bằng \(f( - \frac{m}{4}).\)
Hàm số giảm trên \(( - \infty ; - \frac{m}{4})\) và tăng trên \(( - \frac{m}{4}; + \infty )\)
Theo giả thiết, ta có:
Hàm số giảm trên khoảng \(\left( { - \infty ;1} \right)\)\( \Rightarrow \left( { - \infty ;1} \right) \subset ( - \infty ; - \frac{m}{4}) \Leftrightarrow 1 \le - \frac{m}{4}.\)
Tương tự hàm số tăng trên khoảng \(\left( {1; + \infty } \right)\)\( \Rightarrow \left( {1; + \infty } \right) \subset ( - \frac{m}{4}; + \infty ) \Leftrightarrow - \frac{m}{4} \le 1.\)
Do đó: \( - \frac{m}{4} = 1\) hay \(m = - 4\)
Lại có: Tập giá trị là \([9; + \infty )\)\( \Rightarrow \)Giá trị nhỏ nhất của hàm số bằng 9.
\( \Leftrightarrow f(1) = f( - \frac{m}{4}) = 9 \Leftrightarrow {2.1^2} + ( - 4).1 + n = 9 \Leftrightarrow n = 11.\)
Vậy \(m = - 4,n = 11.\)
Đúng 0
Bình luận (0)
Cho f(x) biết rằng
y
f
’
(
x
-
2
)
+
2
có đồ thị như hình vẽ bên. Hỏi hàm số f(x) nghịch biến trên khoảng nào trong các khoảng dưới đây? A. (-∞;2) B.
3
2
;
5
2
C. (2;+∞) D. (-1;1)
Đọc tiếp
Cho f(x) biết rằng y = f ’ ( x - 2 ) + 2 có đồ thị như hình vẽ bên. Hỏi hàm số f(x) nghịch biến trên khoảng nào trong các khoảng dưới đây?
A. (-∞;2)
B. 3 2 ; 5 2
C. (2;+∞)
D. (-1;1)
Cho hàm số F(x) là một nguyên hàm của hàm số
f
x
2
cos
x
−
1
sin
2
x
trên khoảng
0
;
π
Biết rằng giá trị lớn nhất của F(x) trên khoảng
0
;...
Đọc tiếp
Cho hàm số F(x) là một nguyên hàm của hàm số f x = 2 cos x − 1 sin 2 x trên khoảng 0 ; π Biết rằng giá trị lớn nhất của F(x) trên khoảng 0 ; π là 3 . Chọn mệnh đề đúng trong các mệnh đề sau?
A. F π 6 = 3 3 − 4
B. F 2 π 3 = 3 2
C. F π 3 = − 3
D. F 5 π 6 = 3 − 3
trên cùng 1 mp cho 4037 điểm biết rằng 3 điểm bất kì trong 4037 điểm trên luôn chọn được 2 điểm có khoảng cách nhỏ hơn 1. CMR trong các điểm nói trên có ít nhất 2019 điểm nằm trong đường tròn bán kính bằng 1
Cho hàm số F(x) là một nguyên hàm của hàm số
f
(
x
)
2
cos
x
-
1
sin
2
x
trên khoảng
0
;
π
. Biết rằng giá trị lớn nhất của F(x) trên khoảng
0...
Đọc tiếp
Cho hàm số F(x) là một nguyên hàm của hàm số f ( x ) = 2 cos x - 1 sin 2 x trên khoảng 0 ; π . Biết rằng giá trị lớn nhất của F(x) trên khoảng 0 ; π là 3 . Chọn mệnh đề đúng trong các mệnh đề sau?

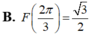
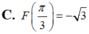
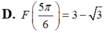
Biết rằng độ dài đường xích đạo khoảng 40 000km. Khoảng cách giữa thành phố Hà Nội và Thành phố Hồ Chí Minh khoảng 2 000km. Độ dài đường xích đạo dài gấp mấy lần khoảng cách giữa hai thành phố trên?
Độ dài đường xích đạo dài gấp số lần khoảng cách giữa hai thành phố trên là:
40 000 : 2 000 = 20 (lần)
Vậy độ dài đường xích đạo dài gấp 20 lần khoảng cách giữa TP Hà Nội và TP Hồ Chí Minh.
Đúng 2
Bình luận (0)
tỉ lệ xích của bản đồ bằng 1/1000000.Tìm khoảng cách giữa 2 thành phố trên bản đồ biết rằng khoảng cách giữa 2 thành phố trên thực tế bằng 94 km
giúp mk vs
ai nhanh mk tk
Khoảng cách giữa hai thanh pho tren bản do la : 94 . \(\frac{1}{1000000}=0,000094\left(km\right)=9,4cm\)
Đúng 0
Bình luận (0)
khoảng cách giữa 2 thành phố trên thực tế là :
94 : 1000000 = 0,000094 ( km ) = 0,094 m
Đáp số : 0,094 m
Đúng 0
Bình luận (0)