a, Xét tam giác ABH và tam giác ACH ta có 

AB = AC (gt) 

AH _ chung

^AHB = ^AHC = 90⁰

Vậy tam giác ABH = tam giác ACH ( ch - cgv ) 

b, Xét tam giác ABC cân tại A

AH là đường cao đồng thời là đường trung tuyến 

=> H là trung điểm BC 

c, Do H là trung điểm BC => HB = 6/2 = 3 cm 

Theo định lí Pytago tam giác AHB vuông tại H

\(AH=\sqrt{AB^2-BH^2}=\sqrt{25-9}=4cm\) 

Hình bạn tự vẽ chắc dc rùi nhé mình chỉ giải thôi 

Bài làm 

a/ \(\Delta\)ABC cân tại A có AM là đường trung tuyến ứng với cạnh BC ( M là trung điểm BC )

Nên  Am cũng là đường cao \(\Rightarrow\)AM \(⊥\)BC

  vì M là trung điểm của BC \(\Rightarrow\)BM= MC = \(\frac{1}{2}BC=\frac{1}{2}.6=3cm\)

Xét tam giác AMB vuông tại M có:

AM² + BM² = AB²

AM² + 3²     = 5²

AM² + 9     =  25

AM²           =  25 - 9 =16

\(\Rightarrow\)AM= \(\sqrt{16}=4\)

Vậy S ABC = \(\frac{1}{2}AM.BC\)= ^{\(\frac{1}{2}4.6=12\)}

b/ Xét tứ giác AMCN có :

OA=OC (gt)

OM=ON ( N đối xứng với M qua O )

\(\Rightarrow\)Tứ giác AMCN là hình bình hành

Mà AM \(⊥\)MC ( chứng minh ở câu a ) \(\Rightarrow\)\(\widehat{AMC}\)= 90 ⁰

Hình bình hành AMCN có \(\widehat{AMC}=90\)nên AMCN là hình chữ nhật

C/ Để AMNC là hình vuông thì AM phải bằng MC ( Vì theo lý thuyết hcn có 2 cạnh kề bằng nhau là hình vuông )

Nếu tam giác ABC vuông cân tại A thì có :

AM là đường trung tuyến ứng với cạnh huyền BC nên BM = AM = MC 

Vậy để tứ giác AMCN là hình vuông thì tam giác ABC phải là tam giác vuông cân tại A

a: Xét ΔAMB và ΔAMC có

AM chung

MB=MC

AB=AC

=>ΔAMB=ΔAMC

b: BM=CM=3cm

=>AM=4cm

c: Xét ΔHBC có

HM vừa là đường cao, vừa là trung tuyến

=>ΔHBC cân tại H

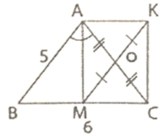
a) Vì M là trung điểm của BC nên:

BM = BC/2 = 6/2 = 3(cm)

Tam giác ABC cân tại A, lại có AM là đường phân giác nên AM cũng là đường cao. Do đó tam giác AMB vuông tại M.

Suy ra: AM2 = AB2 - BM2 (Định lí Pytago)

= 52 - 32 = 16(cm)

Suy ra AM = 4cm

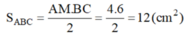
b) ΔAMC vuông tại M có MO là đường trung tuyến nên OM = OA.

Suy ra ∠OAM = ∠OMA ( ΔAMO cân tại O)

Lại có ∠OAM = ∠MAB (AM là tia phân giác góc BAC)

Suy ra ∠OMA = ∠MAB

Mà đây là 2 góc ở vị trí so le trong

Suy ra OM // AB

Vậy tứ giác ABMO là hình thang.

c) Tứ giác AMCK có OA = OC; OM = OK nên tứ giác AMCK là hình bình hành . Lại có ∠AMC = 90o (chứng minh trên) nên tứ giác AMCK là hình chữ nhật.

Hình chữ nhật AMCK là hình vuông

⇔ AM = MC = BM

⇔ AM = BC/2

⇔ ΔABC vuông cân tại A.

a: Xét ΔABH vuông tại H và ΔACH vuông tại H có

AB=AC

AH chung

DO đó: ΔABH=ΔACH

b: BH=CH=BC/2=3cm

=>AH=4(cm)

c: Xét ΔABC có

H là trung điểm của BC

HM//AC

Do đó: M là trung điểm của AB