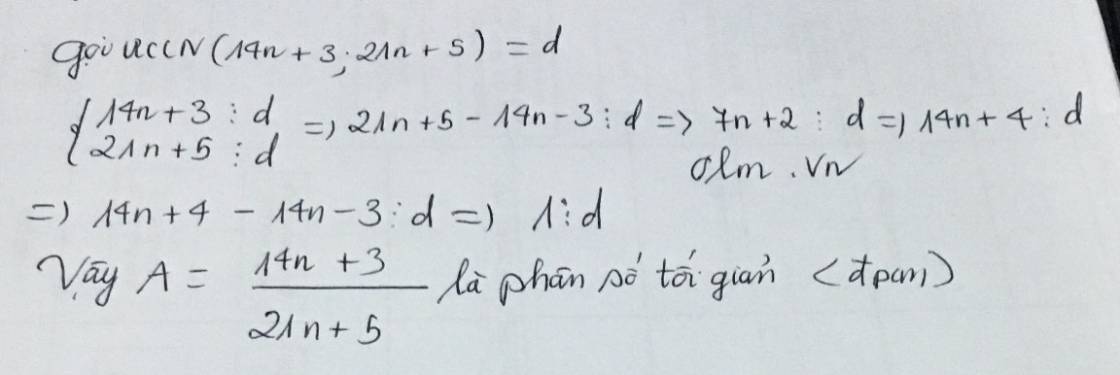Cho n\(\in\)N chứng tỏ: \(A = {14n+3 {} \over 21n+3}\)là phân số tối giản

Những câu hỏi liên quan
Cho n thuộc N chứng tỏ: \(A= {14n+3{} \over 21n+5}\) là phân số tối giản
Cho n thuộc N, Chứng tỏ rằng phân số 14n+3/21n+5 là phân số tối giản.
Đặt \(\left(14n+3,21n+5\right)=d\).
Suy ra
\(\hept{\begin{cases}14n+3⋮d\\21n+5⋮d\end{cases}}\Rightarrow2\left(21n+5\right)-3\left(14n+3\right)=1⋮d\Rightarrow d=1\).
Do đó ta có đpcm.
Cho n thuộc N. Chứng tỏ rằng phân số: 14n+3/21n+5 là phân số tối giản
Gọi d = ƯCLN ( 14n + 3 , 21n + 5 )
Xét hiệu :
\(\left(21n+5\right)-\left(14n+3\right)⋮d\)
\(2\left(21n+5\right)-3\left(14+3\right)⋮d\)
\(42n+10-42n-9⋮d\)
\(10-9⋮d\)
\(1⋮d\)
\(\Rightarrow d\inƯ\left(1\right)\)
\(\RightarrowƯ\left(1\right)=1\Rightarrow d=1\)
Vậy....
#Louis
Đúng 0
Bình luận (0)
cho n thuộc N. chứng tỏ
14n+ 3/21n+5 là phân số tối giản
Gọi \(d\inƯC\left(14n+3,21n+5\right)\)
\(\Rightarrow\hept{\begin{cases}\left(14n+3\right)⋮d\\\left(21n+5\right)⋮d\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}3\left(14n+3\right)⋮d\\2\left(21n+5\right)⋮d\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\left(42n+9\right)⋮d\\\left(42n+10\right)⋮d\end{cases}}\)
\(\Rightarrow\left(42n+10\right)-\left(42+9\right)⋮d\)
\(\Rightarrow1⋮d\)
\(\Rightarrow d\in\left\{1\right\}\)
\(\Rightarrow1\inƯC\left(14n+3,21n+5\right)\)
\(\Rightarrow\frac{14n+3}{21n+5}\)là phân số tối giản
Đúng 0
Bình luận (0)
CHỨNG TỎ RẰNG:\(\dfrac{14n+3}{21n+5}\) LÀ PHÂN SỐ TỐI GIẢN VỚI MỌI n∈Z
Giả sử UCLN(14n+3;21n+5)=d
14n+3 chia hết cho d nên 42n+9 chia hết cho d
21n+5 chia hết cho d nên 42n+10 chia hết cho d
vay 1 chia hết cho d, d=1
Vậy phân số tối giản
Đúng 1
Bình luận (0)
Giải:
Gọi ƯC(14n+3;21n+5)=d
⇒14n+3 ⋮ d ⇒3.(14n+3) ⋮ d ⇒42n+9 ⋮ d
21n+5 ⋮ d 2.(21n+5) ⋮ d 42n+10 ⋮ d
⇒(42n+10)-(42n+9) ⋮ d
⇒ 1 ⋮ d
⇒d=1
Vậy 14n+3/21n+5 là phân số tối giản.
Chúc bạn học tốt!
Đúng 1
Bình luận (0)
chứng tỏ B=\(\dfrac{14n+3}{21n+5}\)(n ϵ N) là phân số tối giản😁
giúp mình nhé!!!
Gọi d=ƯCLN(14n+3;21n+5)
=>42n+9-42n-10 chia hết cho d
=>-1 chia hết cho d
=>d=1
=>PSTG
Đúng 1
Bình luận (1)
Gọi ƯCLN (14n + 3 ; 21n + 5) = d
=> 14n + 3 chia hết cho d => 3(14n + 3) chia hết cho d
21n + 5 chia hết cho d => 2(21n + 5) chia hết cho d
=>2(21n + 5) - 3(14n + 3) chia hết cho d
=> (42n + 10) - (42n + 9) chia hết cho d
=> d = ±1
Đúng 1
Bình luận (0)
Cho n ∈ N , Chứng tỏ rằng phân số \(\frac{14n+3}{21n+5}\) là phân số tối giản
Gọi ƯCLN (14n + 3 ; 21n + 5) = d
=> 14n + 3 chia hết cho d => 3(14n + 3) chia hết cho d
21n + 5 chia hết cho d => 2(21n + 5) chia hết cho d
=>2(21n + 5) - 3(14n + 3) chia hết cho d
=> (42n + 10) - (42n + 9) chia hết cho d
=> d = ±1
=> \(\frac{14n+3}{21n+5}\) là phân số tối giản
Đúng 0
Bình luận (0)
Các bạn xem mình làm có đúng không ??
Đặt d = ƯCLN ( 14n + 3,21n + 5 ) ( d ∈ ℕ* )
Ta có : 14 n + 3 ⋮ d và 21n + 5 ⋮ d
⇒ 3( 14n + 3 ) ⋮ và 2( 21n + 5 ) ⋮ d ⇒ 42n + 9 ⋮ d và 42n + 10 ⋮ d
⇒ (42n + 10) - (42n + 9) ⋮ d ⇒ 1 ⋮ d . Do đó : d = 1
Vậy phân số trên là phân số tối giản
Đúng 0
Bình luận (0)
Đặt z = ƯCLN (14n + 3, 21n + 5) ( z ∈ ℕ*)
Ta có : 14n + 3 ⋮ z và 21n + 5 ⋮ z
⇒ 3(14n + 3 ) ⋮ z và 2(21n + 5 ) ⋮ z ⇒ 42n + 9 ⋮ z và 42n + 10 ⋮ z
⇒ (42n + 10) - (42n + 9) ⋮ z ⇒ 1 ⋮ z. Do đó: z = 1
Vậy phân số trên là phân số tối giản
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng tỏ rằng: \(\frac{14n+3}{21n+5}\)là phân số tối giản với mọi n thuộc Z
Cho n \(\in\)N chứng tỏ: \(A=\dfrac {14n+3}{21n+5}\) là phân số tối giản