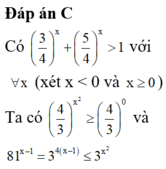Với x<11 rút gọn bt \(\sqrt{121-22x+x^2}\) +x-11

Những câu hỏi liên quan
Khoanh tròn vào chữ cái trước khẳng định đúng.Bỏ dấu giá trị tuyệt đối của biểu thức |x−2| ta được biểu thức:A. x – 2 với x 2 và 2 – x với x 2B. x – 2 với x
≥
2 và 2 – x với x 2C. x – 2 với x 0 và 2 – x với x 0D. x – 2 với x
≥
0 và 2 – x với x 0
Đọc tiếp
Khoanh tròn vào chữ cái trước khẳng định đúng.
Bỏ dấu giá trị tuyệt đối của biểu thức |x−2| ta được biểu thức:
A. x – 2 với x > 2 và 2 – x với x < 2
B. x – 2 với x ≥ 2 và 2 – x với x < 2
C. x – 2 với x > 0 và 2 – x với x < 0
D. x – 2 với x ≥ 0 và 2 – x với x < 0
Khoanh tròn vào chữ cái trước khẳng định đúng.
Bỏ dấu giá trị tuyệt đối của biểu thức |−5x| ta được biểu thức:
A. -5x với x > 0 và 5x với x < 0
B. -5x với x ≥ 0 và 5x với x < 0
C. 5x với x > 0 và -5x với x < 0
D. -5x với x ≤ 0 và 5x với x > 0
Tìm các số nguyên x biết
a) |x-1| = 6 với x > 1
b) |x+2| = 3 với x > 0
c) x + |3 - x| = 7 với x > 3
a) |x-1| = 6 với x > 1
Do x > 1 nên x + 1 > 0. Từ đó | x - 1| = x – 1 (Giá trị tuyệt đối của một số nguyên dương)
Theo đề bài, ta có: x – 1 = 6 hay x = 7
b) |x+2| = 3 với x > 0
Do x > 0 nên x + 2 > 0. Từ đó b) |x + 2| = x + 2 (Giá trị tuyệt đối của một số nguyên dương)
Theo đề bài, ta có: x + 2 = 3 hay x =1
c) x + |3 - x| = 7 với x > 3
Do x > 3 nên 3 - x là một nguyên âm. Từ đó |3 - x| = - (3 - x)
Theo đề bài, ta có:
x + |3 - x| = 7
x + x - 3 = 7
x\(^2\) = 7 + 3 = 10
x = 10 : 2 = 5
Đúng 2
Bình luận (0)
Giải:
a)
|x-1| = 6 với x > 1
Do x > 1 nên x + 1 > 0. Từ đó | x - 1| = x – 1 (Giá trị tuyệt đối của một số nguyên dương)
Theo đề bài, ta có: x – 1 = 6 hay x = 7
b) |x+2| = 3 với x > 0
Do x > 0 nên x + 2 > 0. Từ đó b) |x + 2| = x + 2 (Giá trị tuyệt đối của một số nguyên dương)
Theo đề bài, ta có: x + 2 = 3 hay x =1
c) x + |3 - x| = 7 với x > 3
Do x > 3 nên 3 - x là một nguyên âm. Từ đó |3 - x| = - (3 - x)
Theo đề bài, ta có:
x + |3 - x| = 7
x + x - 3 = 7
x2 = 7 + 3 = 10
x =10:2=5
Đúng 0
Bình luận (3)
1) x+(16/x-2) với x>2
2) 5x+ (180/x-1) với x>1
3) x/2 +(2x/x-1) với x >1
4) 2/2-x +(1/x) với 0<x<2
Giúp mình với. đề là tìm gtnn
Có bao nhiêu mệnh đề dưới đây là đúng?
3
x
2
x
v
ớ
i
∀
x
∈
ℝ
4
x
2
≥
3
x
2
v
ớ
i
∀
x
∈
ℝ
81
x
-
1
≤
3
x...
Đọc tiếp
Có bao nhiêu mệnh đề dưới đây là đúng?
3 x > 2 x v ớ i ∀ x ∈ ℝ 4 x 2 ≥ 3 x 2 v ớ i ∀ x ∈ ℝ 81 x - 1 ≤ 3 x 2 v ớ i ∀ x ∈ ℝ 5 x + 3 x > 4 x v ớ i ∀ x ∈ ℝ 2 x + 3 x < 5 x v ớ i ∀ x > 1
A. 2
B. 3
C. 4
D. 5
Bỏ dấu GTTĐ
a) /x/ với x > 0
b) /x/ với x < 0
c) / x + 1 / với x > 0
d) / x - 3 / với x > 3
e) / x - 5 / với x < 5
g) / x + 2 / với x < -2
cho x và y tỉ lệ nghịch với nhau với x=5 , y = 1/2 . Tìm h có hệ số tỉ lệ của y với x , biểu diên x theo y , y theo x, với x=-3 . tìm y , với y = -6 tìm x
a: Vì x và y tỉ lệ nghịch
nên hệ số tỉ lệ của y đối với x là \(h=x\cdot y=5\cdot\dfrac{1}{2}=\dfrac{5}{2}\)
b:\(x\cdot y=\dfrac{5}{2}\)
=>\(y=\dfrac{5}{2x};x=\dfrac{5}{2y}\)
Khi x=-3 thì \(y=\dfrac{5}{2\cdot\left(-3\right)}=\dfrac{5}{-6}=-\dfrac{5}{6}\)
Khi y=-6 thì \(x=\dfrac{5}{2\cdot\left(-6\right)}=\dfrac{5}{-12}=-\dfrac{5}{12}\)
Đúng 0
Bình luận (0)
tìm giá trị nhỏ nhất của các biểu thức sau:a Adfrac{x^3+2021}{x} với x0b B4x+dfrac{25}{x-1}với x1c Cdfrac{3x^4+16}{x^3}với x0d Dx+dfrac{1}{x}với x lớn hơn bằng 2e Edfrac{9x}{2-x}+dfrac{2}{x}với 0x2f Fdfrac{3}{1-x}+dfrac{4}{x}với 0x1
Đọc tiếp
tìm giá trị nhỏ nhất của các biểu thức sau:
a A=\(\dfrac{x^3+2021}{x}\) với x>0
b B=\(4x+\dfrac{25}{x-1}\)với x>1
c C=\(\dfrac{3x^4+16}{x^3}\)với x>0
d D=\(x+\dfrac{1}{x}\)với x lớn hơn bằng 2
e E=\(\dfrac{9x}{2-x}+\dfrac{2}{x}\)với 0<x<2
f F=\(\dfrac{3}{1-x}+\dfrac{4}{x}\)với 0<x<1
a.
\(A=x^2+\dfrac{2021}{x}=x^2+\dfrac{2021}{2x}+\dfrac{2021}{2x}\ge3\sqrt[3]{\dfrac{2021^2}{4x^2}}=3\sqrt[3]{\dfrac{2021^2}{4}}\)
Dấu "=" xảy ra khi \(x=\sqrt[3]{\dfrac{2021}{3}}\)
b.
\(B=4\left(x-1\right)+\dfrac{25}{x-1}+4\ge2\sqrt{\dfrac{100\left(x-1\right)}{x-1}}+4=24\)
Dấu "=" xảy ra khi \(x=\dfrac{7}{2}\)
c.
\(C=3x+\dfrac{16}{x^3}=x+x+x+\dfrac{16}{x^3}\ge4\sqrt[4]{\dfrac{16x^3}{x^3}}=8\)
\(A_{min}=8\) khi \(x=2\)
Đúng 0
Bình luận (0)
d.
\(D=x+\dfrac{1}{x}=\left(\dfrac{x}{4}+\dfrac{1}{x}\right)+\dfrac{3}{4}.x\ge2\sqrt{\dfrac{x}{4x}}+\dfrac{3}{4}.2=\dfrac{5}{2}\)
Dấu "=" xảy ra khi \(x=2\)
e.
\(E=\dfrac{9\left(x-2\right)+18}{2-x}+\dfrac{2}{x}=2\left(\dfrac{1}{x}+\dfrac{9}{2-x}\right)-9\ge\dfrac{2.\left(1+3\right)^2}{x+2-x}-9=7\)
\(E_{min}=7\) khi \(x=\dfrac{1}{5}\)
f.
\(F=\dfrac{3}{1-x}+\dfrac{4}{x}\ge\dfrac{\left(\sqrt{3}+2\right)^2}{1-x+x}=7+4\sqrt{3}\)
Dấu "=" xảy ra khi \(x=4-2\sqrt{3}\)
Đúng 0
Bình luận (0)
Cho hàm số :
f
x
x
2
x
v
ớ
i
x
1
,
x
≠
0...
Đọc tiếp
Cho hàm số : f x = x 2 x v ớ i x < 1 , x ≠ 0 0 v ớ i x = 0 x v ớ i x ≥ 1
A. Mọi điểm thuộc R
B. Mọi điểm trừ x=0
C. Mọi điểm trừ x=1
D. Mọi điểm trừ x=0 và x=1
Tính giá trị của (x2-5)(x+3)+(x+4)(x+x2)
a)Với x=0
b)Với x=15
c)Với x=-15
d)Với x=0,15