chứng minh định lí:Trong một tam giác, có ba đường trung tuyến cùng nhau tại một điểm. điểm đó cách đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.
Những câu hỏi liên quan
Chứng minh định lí:
Ba đường trung tuyến của một tam giác cùng đi qua một điểm.
Điểm đó cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.
Giao điểm của ba đường trung tuyến gọi là trọng tâm
GT : G là trọng tâm ∆ ABC
KL:\(\frac{AG}{AD}=\frac{BG}{BE}=\frac{CG}{CF}=\frac{2}{3}\)
Đúng 0
Bình luận (0)
trong tam giác ta có các cạnh như : AG;GD;AE;EC.....
theo hình vẽ như bạn Hoàn g Q V
ta có: AG là 2 phần và AD là 3 phần
=>\(\frac{AG}{AD}=\frac{2}{3}\)
=>(ĐPCM)
Đúng 0
Bình luận (0)
CMR: Ba đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy
Có ai biết cách chứng minh định lý ba đường trung tuyến này không?
"Ba đường trung tuyến của một tam giác đồng quy tại một điểm, điểm đó gọi là trọng tâm của tam giác. Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng \(\frac{2}{3}\)độ dài đường trung tuyến đi qua đỉnh ấy
Điền số thích hợp vào chỗ trống: “Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng … độ dài đường trung tuyến đi qua đỉnh ấy”
A. 2/3
B. 3/2
C. 3
D. 2
Định lý: Vị trí trọng tâm: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy
Số cần điền là 2/3.
Chọn đáp án A.
Đúng 0
Bình luận (0)
1 tháng 4 2015 lúc 17:29
Chứng minh rằng: Điểm cách đều ba đỉnh của một tam giác vuông là trung điểm của cạnh huyền của tam giác đó.
Từ đó hãy tính độ dài đường trung tuyến xuất phát từ đỉnh góc vuông theo độ dài cạnh huyền của một tam giác vuông.
Sử dụng bài 55 để chứng minh rằng: Điểm cách đều ba đỉnh của một tam giác vuông là trung điểm của cạnh huyền của tam giác đó.
Từ đó hãy tính độ dài đường trung tuyến xuất phát từ đỉnh góc vuông theo độ dài cạnh huyền của một tam giác vuông.
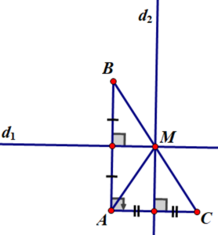
+ Giả sử ∆ABC vuông tại A.
d1 là đường trung trực cạnh AB, d2 là đường trung trực cạnh AC.
d1 cắt d2 tại M. Khi đó M là điểm cách đều ba đỉnh của tam giác ABC.
+ Áp dụng kết quả bài 55 ta có B, M, C thẳng hàng.
QUẢNG CÁO+ M cách đều A, B, C ⇒ MB = MC ⇒ M là trung điểm của cạnh BC (đpcm)
+ M là trung điểm của cạnh BC (đpcm)
*) Giả sử AM là trung tuyến của tam giác ABC suy ra M là trung điểm của cạnh BC
⇒ MB = MC = BC/2
Mà MA = MB = MC (cmt)
⇒ MA = BC/2
Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền.
Đúng 0
Bình luận (0)
chứng minh rằng trọng tâm của tam giác cách các đỉnh bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy
Cho tam giác ABC có AM và BN là hai đường trung tuyến cắt nhau tại G. Khẳng định nào sau đây đúng? (có thể chọn nhiều đáp án) *
Điểm G cách đều ba đỉnh của tam giác
Điểm G gọi là trọng tâm của tam giác
GA = 2.GM
Điểm G cách đỉnh B một khoảng bằng 2/3 độ dài đường trung tuyến BN
GA = GB
GN = 3.BN
Cho tam giác ABC có AM và BN là hai đường trung tuyến cắt nhau tại G. Khẳng định nào sau đây đúng? (có thể chọn nhiều đáp án) *
Điểm G cách đều ba đỉnh của tam giác
Điểm G gọi là trọng tâm của tam giác
GA = 2.GM
Điểm G cách đỉnh B một khoảng bằng 2/3 độ dài đường trung tuyến BN
GA = GB
GN = 3.BN
Đúng 0
Bình luận (0)
Cho tam giác ABC có AM và BN là hai đường trung tuyến cắt nhau tại G. Khẳng định nào sau đây đúng? (có thể chọn nhiều đáp án) *
Điểm G cách đều ba đỉnh của tam giác
Điểm G gọi là trọng tâm của tam giác
GA = 2.GM
Điểm G cách đỉnh B một khoảng bằng 2/3 độ dài đường trung tuyến BN
GA = GB
GN = 3.BN
Đúng 0
Bình luận (0)
Sử dụng bài 55 để chứng minh rằng : Điểm cách đều ba đỉnh của một tam giác vuông là trung điểm của cạnh huyền của tam giác đó
Từ đó hãy tính độ dài đường trung tuyến xuất phát từ đỉnh góc vuông theo độ dài cạnh huyền của một tam giác vuông ?
a) Giả sử ∆ABC vuông góc tại A. Vẽ hai đường trung trực của hai cạnh góc vuông AB, AC cắt nhau tại M. Ta chứng minh M là trung điểm của BC.
Vì M là giao điểm hai đường trung trực d1, d2
của AB, AC mà AB ⊥ AC nên B, M, C thẳng hàng (bài tập 55)
Vì MA = MB (M thuộc đường trung trực của AB)
MA = MC (M thuộc đường trung trực của AC)
=> MB = MC
Do B, M, C thẳng hàng và M cách đều BC nên M là trung điểm của BC
b) M là trung điểm Bc => MB = 1212 BC
mà AM = MB nên MA =1212 BC
Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền.
Đúng 0
Bình luận (0)
a) Giả sử ∆ABC vuông góc tại A. Vẽ hai đường trung trực của hai cạnh góc vuông AB, AC cắt nhau tại M. Ta chứng minh M là trung điểm của BC.
Vì M là giao điểm hai đường trung trực d1, d2
của AB, AC mà AB ⊥ AC nên B, M, C thẳng hàng (bài tập 55)
Vì MA = MB (M thuộc đường trung trực của AB)
MA = MC (M thuộc đường trung trực của AC)
=> MB = MC
Do B, M, C thẳng hàng và M cách đều BC nên M là trung điểm của BC
b) M là trung điểm Bc => MB = 1212 BC
mà AM = MB nên MA =1212 BC
Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền
Đúng 0
Bình luận (1)