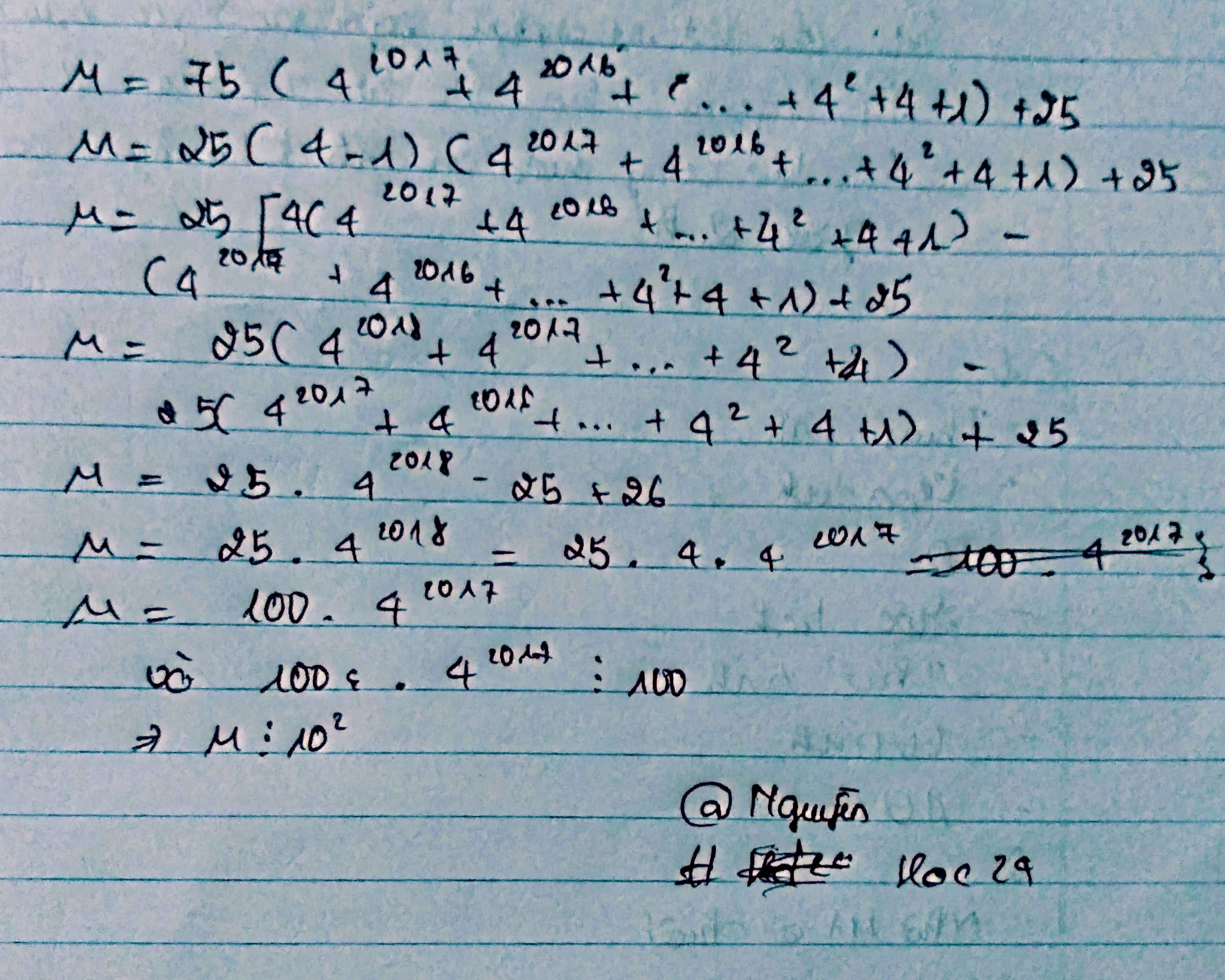cho B =4+4^2+4^3+4^4+.................4^2016 chứng tỏ B chia hết cho 105

Những câu hỏi liên quan
cho C= 4+4^2 +4^3+4^4+...........+4^2015+4^2016
chứng minh C chia hết cho 105
ta có 4+4^2+...+4^2016
=>(4+4^2+4^3+4^4+4^5+4^6)+(4^7+4^8+4^9+4^10+4^11+4^12)+...+(4^2011+4^2012+4^2013+4^2014+4^2015+4^2016)
=>4.(1+4+4^2+4^3+4^4+4^5)+4^7.(1+4+4^2+4^3+4^4+4^5)+...+4^2011.(1+4+4^2+4^3+4^4+4^5)
=>4.1365+4^7.1365+...+4^2011.1365
=>1365.(4+4^7+...+4^2011)chia hết cho 105 vì 1365 chia hết cho 105
Vậy C chia hết cho 105
Đúng 0
Bình luận (0)
ta có:4+4^2+4^3+....+4^2016=4^1+4^2+4^3+....+4^2016
=>có (2016-1):1+1=2016 số số hạng
C=(4+4^2+4^3+4^4+4^5+4^6)+(4^7+4^8+4^9+4^10+4^11+4^12)+....+(4^2011+4^2012+4^2013+4^2014+4^2015+4^2016)
C=4(1+4+4^2+
sorry nha mình bận
Đúng 0
Bình luận (0)
chứng tỏ rằng
a) A=49+105+399 chia hết cho 7
b) B=84+48+120 không chia hết cho 8
c) C=125 nhân 11+50 nhân 34 chia hết cho 25
d) D= 1+4+4 mũ 2+4 mũ 3 +...........+4 mũ 10 +4 mũ 11 chia hết cho21
Chứng tỏ rằng :
A) 5 mũ 2016 + 5 mũ 2015 + 5 mũ 2016 chia hết cho 31
B) 1+7+7 mũ 2 + 7 mũ 3+ .....+7 mũ 701 chia hết cho 8
C) 4 mũ 39 + 4 mũ 40+ 4 mũ 41 chia hết cho 28
1+7+7 mũ 2+7 mũ 3......+7 mũ 100.Tính a,a là tổng dãy số trên
Đúng 0
Bình luận (0)
Cho C = \(4^1+4^2+4^3+4^4+..+4^{2016}\) .
Chứng minh C chia hết cho 105. help me
Cách làm như sau:
-Chứng minh C chia hết cho 5 bằng cách nhóm 2 số vào một cặp
-Chứng minh C chia hết cho 21 bằng cách nhóm 3 số vào một cặp
Mà 21 và 5 nguyên tố cùng nhau =>C chia hết cho 21.5 => C chia hết cho 105(đpcm)
Đúng 0
Bình luận (0)
Ta có :
\(C=4^1+4^2+4^3+4^4+...+4^{2016}\)
\(C=\left(4^1+4^2\right)+\left(4^2+4^3\right)+...+\left(4^{2015}+4^{2016}\right)\)
\(C=4\left(1+4\right)+4^2\left(1+4\right)+...+4^{2015}\left(1+4\right)\)
\(C=4.5+4^2.5+...+4^{2015}.5\)
\(C=5\left(4+4^2+...+4^{2015}\right)⋮5\) \(\left(1\right)\)
Lại có :
\(C=4^1+4^2+4^3+4^4+...+4^{2016}\)
\(C=\left(4^1+4^2+4^3\right)+\left(4^4+4^5+4^6\right)+...+\left(4^{2014}+4^{2015}+4^{2016}\right)\)
\(C=4\left(1+4+16\right)+4^4\left(1+4+16\right)+...+4^{2014}\left(1+4+16\right)\)
\(C=4.21+4^4.21+...+4^{2014}.21\)
\(C=21\left(4+4^4+...+4^{2014}\right)⋮21\) \(\left(2\right)\)
Từ (1) và (2) suy ra : \(C⋮5\) và \(C⋮21\)
\(\Rightarrow\)\(C⋮5.21=105\)
\(\Rightarrow\)\(C⋮105\)
Vậy \(C⋮105\)
Chúc bạn học tốt ~
Đúng 0
Bình luận (0)
Cho B=4^1+4^2+4^3+...+4^20 Chứng tỏ B Chia hết cho 5
Cho C=7+7^2+7^3+...7^20 Chứng tỏ C chia hết cho 8
\(B=4+4^2+4^3+...+4^{20}\)
\(=\left(4+4^2\right)+\left(4^3+4^4\right)+...+\left(4^{19}+4^{20}\right)\)
\(=4.\left(1+4\right)+4^3.\left(1+4\right)+....+4^{19}.\left(1+4\right)\)
\(=5.\left(4+4^3+...+4^{19}\right)⋮5\)
Vậy B chia hết cho 5
\(C=\left(7+7^2\right)+\left(7^3+7^4\right)+...+\left(7^{19}+7^{20}\right)\)
\(=7.\left(1+7\right)+7^3.\left(1+7\right)+....+7^{19}.\left(1+7\right)\)
\(=7.8+7^3.8+...+7^{19}.8\)
\(=8.\left(7+7^3+...+7^{19}\right)⋮8\)
Vậy C chia hết cho 8
Đúng 1
Bình luận (0)
mình chưa học đến thông cảm nhé
Chứng tỏ rằng :
a . nếu 2 STN a và 2a đều có tổng các chữ số là k thì a chia hết cho 9
b . A = ( n + 20162017 ) . ( n + 21072016 ) chia hết cho 2 với mọi STN
c . B =75 . ( 4120 + 4119 + 4118 + ...... + 43 + 42 + 4 +1 ) +25 chia hết cho M
Bài 1:
a) Cho C = 4 + 4^2 + 4^3 + 4^4 + ... + 4^2015 + 4^2016 . Chứng minh C chia hết cho 21 và 105
b) Chứng minh rằng với mọi số tự nhiên khác 0 có số lượng các ước tự nhiên là một số lẻ thì số tự nhiên đó là số chính phương
Bài 1:
a) C = 4 + 42 + 43 + 44 + ... + 42015 + 42016
C = (4 + 42 + 43) + (44 + 45 + 46) + ... + (42014 + 42015 + 42016)
C = 4(1 + 4 + 42) + 44 ( 1 + 4 + 42) + ...+ 42014(1 + 4 + 42)
C = 4 . 21 + 44 . 21 + ... + 42014 . 21
C = 21(4 + 44 + ... + 42014) \(⋮\)21
=> C \(⋮\)21
C = 4 + 42 + 43 + 44 + 45 + ... + 42015 + 42016
C = (4 + 42 + 43 + 44 + 45 + 46) + ... + (42011 + 42012 + 42013 + 42014 + 42015 + 42016)
C = 4(1 + 4 + 42 + 43 + 44 + 45) + ... + 42011(1 + 4 + 42 + 43 + 44 + 45)
C = 4 . 1365 + 47 . 1365 + ... + 42011 . 1365
C = 1365(4 + 47 + ... + 42011)
mà 1365 \(⋮\)105
=> C \(⋮\)105
Đúng 0
Bình luận (0)
Cho A = 1 + 4 + 4^2 + 4^3 +...+ 4^11 chứng minh:
a) A chia hết cho 21
b) A chia hết cho 105
c) A chia hết cho 4097
a)A=1+4+4/\2+.........+4/\11
=(1+4+4/\2)+.....+(4/\9+4/\10+4/\11)
=21+..............+4/\9.(1+4+4/\2)
=21+..+4/\9.21
=(1+4/\3+....+4/\9).21chia hết cho 21
Đúng 0
Bình luận (0)
Chứng tỏ rằng \(M=75.\left(4^{2017}+4^{2016}+...+4^2+4+1\right)+25\) chia hết cho 102