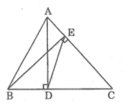
Tam giác ABC có 2 đường cao là AD và BE (D ∈ BC, E ∈ AC).
Chứng minh ΔDEC ∽ ΔABC

Những câu hỏi liên quan
Tam giác ABC có hai đường cao là AD và BE (D thuộc BC và E thuộc AC). Chứng minh hai tam giác DEC và ABC là hai tam giác đồng dạng.
Xét △ ADC và △ BEC, ta có:
∠ (ADC) = ∠ (BEC) = 90 0
∠ C chung
Suy ra: △ ADC đồng dạng △ BEC (g.g)
Suy ra: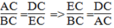 ⇒ ECBC = DCAC
⇒ ECBC = DCAC
Xét △ DEC và △ ABC ta có:
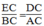
∠ C chung
Vậy △ DEC đồng dạng △ ABC (c.g.c)
Đúng 0
Bình luận (0)
Tam giác ABC có hai đường cao là AD và BE (D thuộc BC, E thuộc AC). Chứng minh hai tam giác DEC và ABC là hai tam giác đồng dạng ?
Cho ΔABC , AB=AC , phân giác AD .
a, Chứng minh : ΔABD=ΔACD
b, Vẽ trung tuyến CF , G là giao điểm CF và AD . Chứng minh G là trọng tâm ΔABC
c, Gọi H là trung điểm của CD . Đường thẳng \(\perp\)CD tại H cắt AC tại E . Chứng minh : ΔDEC cân
d, So sánh AD và BD
a) Xét ΔABD và ΔACD có
AB=AC(ΔBAC cân tại A)
\(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác của \(\widehat{BAC}\))
AD chung
Do đó: ΔABD=ΔACD(c-g-c)
b) Ta có: ΔABD=ΔACD(cmt)
nên BD=CD(hai cạnh tương ứng)
hay D là trung điểm của BC
Xét ΔABC có
AD là đường trung tuyến ứng với cạnh BC(cmt)
CF là đường trung tuyến ứng với cạnh AB(gt)
AD cắt CF tại G(gt)
Do đó: G là trọng tâm của ΔABC(Tính chất ba đường trung tuyến của tam giác)
c) Ta có: ΔABD=ΔACD(cmt)
nên \(\widehat{ADB}=\widehat{ADC}\)(hai góc tương ứng)
mà \(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)
nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
Xét ΔADC có
H là trung điểm của CD(gt)
HE//AD(cùng vuông góc với BC)
Do đó: E là trung điểm của AC(Định lí 1 về đường trung bình của tam giác)
Ta có: ΔADC vuông tại D(cmt)
mà DE là đường trung tuyến ứng với cạnh huyền AC(E là trung điểm của AC)
nên \(DE=\dfrac{AC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
hay DE=EC
Xét ΔDEC có ED=EC(cmt)
nên ΔDEC cân tại E(Định nghĩa tam giác cân)
Đúng 0
Bình luận (2)
Cho tam giác ABC cân tại A, có góc BAC nhọn. Qua A vẽ tia phân giác của góc BAC cắt cạnh BC tại D. a) Chứng minh ΔABD ΔACD. b) Vẽ đường trung tuyến CF của tam giác ABC cắt cạnh AD tại G. Chứng minh G là trọng tâm của tam giác ABC. c) Gọi H là trung điểm của cạnh DC. Qua H vẽ đường thẳng vuông góc với cạnh DC cắt cạnh AC tại E. Chứng minh ΔDEC cân. d) Chứng minh ba điểm B, G, E thẳng hàng và AD BD.
Đọc tiếp
Cho tam giác ABC cân tại A, có góc BAC nhọn. Qua A vẽ tia phân giác của góc BAC cắt cạnh BC tại D. a) Chứng minh ΔABD = ΔACD. b) Vẽ đường trung tuyến CF của tam giác ABC cắt cạnh AD tại G. Chứng minh G là trọng tâm của tam giác ABC. c) Gọi H là trung điểm của cạnh DC. Qua H vẽ đường thẳng vuông góc với cạnh DC cắt cạnh AC tại E. Chứng minh ΔDEC cân. d) Chứng minh ba điểm B, G, E thẳng hàng và AD > BD.
Cho ΔABC. Lấy điểm D, E sao cho C là trung điểm của BE và AD. Chứng minh:
a) ΔABC = ΔDEC; b) AB // DE
c) Nếu ΔABC cân tại C thì ΔAEC là tam giác gì? Vì sao?
cho tam giác ABC cân tại A, có góc A là góc nhọn. Vẽ hai đường cao AD và BE cắt nhau tại H (D thuộc BC, E thuộc AC).
a) chứng minh tam giác ABC = tam giác ACD
b) đường thẳng CH cắt AB tại F. Chứng minh CF là đường cao của tam giác ABC
c) chứng minh EF //BC
Cho tam giác ABC (AB<AC) có đường cao AD (D thuộc BC)
a/ Chứng minh hai tam giác DAB và ACB đồng dạng
b/ Phân giác góc ABC cắt AC tại E, từ C vẽ đường thằng vuông góc với đường thẳng BE tại F chứng minh AE.AB=EC.BD
c/ Kẻ FH vuông AC tại H chứng minh hai góc BCF và HCF bằng nhau
d/ I là trung điểm BC, chứng minh I,H,F thẳng hàng
Sửa đề: ΔABC vuông tại A
a) Xét ΔDAB vuông tại D và ΔACB vuông tại A có
\(\widehat{ABC}\) chung
Do đó: ΔDAB\(\sim\)ΔACB(g-g)
b) Xét ΔABC có
BE là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AE}{EC}=\dfrac{AB}{BC}\)(Định lí đường phân giác của tam giác)(1)
Ta có: ΔDAB\(\sim\)ΔACB(cmt)
nên \(\dfrac{AB}{BC}=\dfrac{BD}{BA}\)(Các cặp cạnh tương ứng tỉ lệ)(2)
Từ (1) và (2) suy ra \(\dfrac{AE}{EC}=\dfrac{BD}{AB}\)
hay \(AE\cdot AB=BD\cdot EC\)(đpcm)
Đúng 1
Bình luận (0)
Cho tam giác ABC nhọn nội tiếp đường tròn tâm O(AB<AC), có ba đường cao AD, BE, CF cắt nhau tại H ( D thuộc BC, E thuộc AC, F thuộc AB)
a) Chứng minh tứ giác BFEC và tứ giác BFHD là các tứ giác nội tiếp
b) Vẽ đường kính AK của (O). Chứng minh AB.AC=AD.AK
a: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
góc BDH+góc BFH=180 độ
=>BDHF nội tiếp
b; góc ACK=1/2*sđ cung AK=90 độ
Xét ΔACK vuông tại C và ΔADB vuông tại D có
góc AKC=góc ABD
=>ΔACK đồng dạng với ΔADB
=>AC/AD=AK/AB
=>AC*AB=AD*AK
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn có AD và BE là hai đường cao cắt nhau tại H a, Chứng minh rằng: AD + BE < BC + AC b, Cho biết: AC < BC. Chứng minh rằng: HA < HB và AC + BE < BC + AD
a: ΔADC vuông tại D
=>AD<AC
ΔBEC vuông tại E
=>BE<BC
=>AD+BE<BC+AC
b: CA<CB
=>góc CAB>gócCBA
=>90 độ-góc CAB<90 độ-góc CBA
=>góc HBA<góc HAB
=>HA<HB
Đúng 0
Bình luận (0)
Cho ΔABC vuông tại A, đường cao AH và đường phân giác AD (H và D thuộc BC). Biết AB = 21cm, AC = 28cm.
a) Tính diện tích tam giác ABC và chứng minh AH . BC = AB . AC
\(S_{ABC}=\dfrac{AB.AC}{2}=\dfrac{21.28}{2}=294\left(cm^2\right)\)
Ta có:\(S_{ABC}=\dfrac{AB.AC}{2}\) mà ta lại có: \(S_{ABC}=\dfrac{AH.BC}{2}\)
\(\Rightarrow\dfrac{AB.AC}{2}=\dfrac{AH.BC}{2}\Rightarrow AB.AC=AH.BC\left(đpcm\right)\)
Đúng 3
Bình luận (4)