Xét △ ADC và △ BEC, ta có:
∠ (ADC) = ∠ (BEC) = 90 0
∠ C chung
Suy ra: △ ADC đồng dạng △ BEC (g.g)
Suy ra: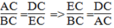 ⇒ ECBC = DCAC
⇒ ECBC = DCAC
Xét △ DEC và △ ABC ta có:
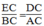
∠ C chung
Vậy △ DEC đồng dạng △ ABC (c.g.c)
Xét △ ADC và △ BEC, ta có:
∠ (ADC) = ∠ (BEC) = 90 0
∠ C chung
Suy ra: △ ADC đồng dạng △ BEC (g.g)
Suy ra: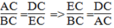 ⇒ ECBC = DCAC
⇒ ECBC = DCAC
Xét △ DEC và △ ABC ta có:
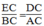
∠ C chung
Vậy △ DEC đồng dạng △ ABC (c.g.c)
Cho tam giác ABC có hai đường cao là AD và BE ( D thuộc BC, E thuộc AC). Chứng minh rằng:
a) tam giác ADC đồng dạng tam giác BEC.
b) AC.EC=BC.DC
c) tam giác DEC đồng dạng tam giác ABC.
Bài: Cho tam giác ABC nhọn với các đường cao AD, BE (D thuộc BC; E thuộc AC). Chứng minh tam giác DEC đồng dạng với tam giác ABC
- Bài này hơi khó, giúp mình nhé, cám ơn !
Câu 1: - cho tam giác ABC . Vẽ MN là đường trung bình của tam giác ABC ( M thuộc AB, N thuộc AC) . Chứng minh tam giác ABC đồng dạng với tam giác AMN
câu 2: cho tam giác ABC có góc A > 90 ( AC > AB) trên cạnh BC, AC lấy 2 điểm D và E sao cho CDE = BAC
A. Chứng minh tam giác ABC đồng dạng tam giác DEC
B. Viết tỉ số đồng dạng cũa tam giác ABC và tam giác DEC
C. Chứng minh DC × BC=EC×AC
Cho tam giác ABC nhọn có ba đường cao AD, BE, CF với D thuộc BC, E thuộc AC, F thuộc AB, Gọi H là trực tâm của tam giác ABC. Chững minh rằng tam giác ABD đồng dạng với tam giác CHD
Cho tam giác ABC có ba góc nhọn, hai đường cao BD và CE của tam giác cắt nhau tại H (D thuộc AC, E thuộc AB)
a) Chứng minh rằng tam giác BHE đồng dạng với tam giác CHD
b) Chứng minh AB.AE = AC.AD
c) Chứng minh góc AED = góc ACB
Cho tam giác ABC vuông tại A có AH là đường cao (H thuộc BC).Biết AB =6cm,Bc=10cm
a,chứng minh rằng tam giác HBA đồng dạng vs tam giác ABC
b,Tính AC,AH,HB
c,I và K lần lượt là hình chiếu của điểmH lên AB, AC. CHứng minh rằng AI .AB=AK.AC
d,Vẽ phân giác của tam giác AD của tam giác ABC ( D thuộc BC).Đường phân giác DE của tam giác ABD(E thuộc AB),đường phân giác DF của tam giác ADC(F thuộc AC) chứng minh rằng EA/EB*DB/DC*FC/FA=1
Cho tam giác ABC vuông tại A (AB<AC) có AH là đường cao (H thuộc cạnh BC).
a, Chứng minh: Tam giác ABC đồng dạng với tam giác HAC và
AC2= BC.HC
b, Gọi CD là tia phân giác góc ACB (D thuộc cạnh AB), E là giao điểm của AH và CD. Chứng minh: AE.AD=HE.BD
Cho tam giác ABC vuông tại A ( AB < AC ), đường cao AH ( H thuộc BC )
1, Chứng minh: Tam giác HBA đồng dạng tam giác ABC và BC2 = BH.BC
2, Kẻ phân giác BE Của góc ABC ( E thuộc AC ), BE cắt AH tại I
Cho tam giác ABC nhọn (AB <AC), đường cao AD (D thuộc BC). Gọi E,F lần lượt là hình chiếu của D trên AB và AC
a) Chứng minh: tam giác ADE đồng dạng tam giác ABD và AE.AB= AD^2
b) Chứng minh: gócAFE= góc ABC
c) Gọi I là giao điểm của FE và CB. Chứng minh: ID^2= IE.IF
giúp e vs ạ