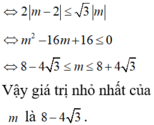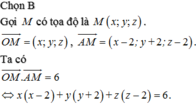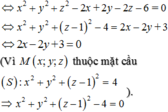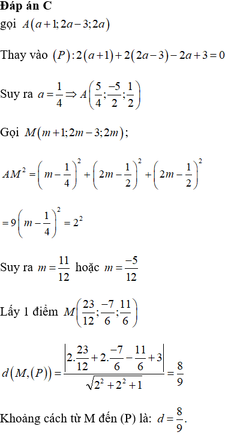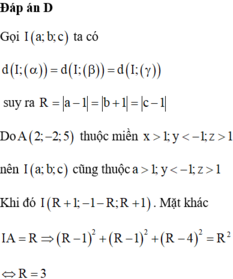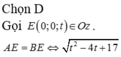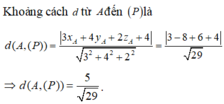Trong không gian Oxyz, cho điểm M(1/2;√3/2;0) và mặt cầu (S):x2+y2+z2=8. Đường thẳng d thay đổi, đi qua điểm M, cắt mặt cầu (S) tại hai điểm A, B phân biệt. Tính diện tích lớn nhất S của tam giác OAB.

Những câu hỏi liên quan
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
(
S
m
)
:
(
x
-
1
)
2
+
(
y
-
1
)
2
+
(
z
-...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu ( S m ) : ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - m ) 2 = m 2 4 và hai điểm A(2;3;5), B(1;2;4). Tìm giá trị nhỏ nhất của m để trên ( S m ) tồn tại điểm M sao cho M A 2 - M B 2 = 9 .
A. m=1
B. m= 3 - 3
C. m= 8 - 4 3
D. m= 4 - 3 2
Trong không gian với hệ trục tọa độ Oxyz cho điểm A(2;-2;2) và mật cầu (S):
x
2
+
y
2
+
(
z
-
1
)
2
4
. Điểm M di chuyển trên mặt cầu (S) đồng thời thỏa mãn
O...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho điểm A(2;-2;2) và mật cầu (S): x 2 + y 2 + ( z - 1 ) 2 = 4 . Điểm M di chuyển trên mặt cầu (S) đồng thời thỏa mãn O M → . A M → = 6 . Điểm M luôn thuộc mặt phẳng nào dưới đây?
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho hai điểm
A
(
-
1
;
1
;
2
)
và
B
(
3
;
-
5
;
0
)
. Tọa độ trung điểm của đoạn thẳng AB là
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A ( - 1 ; 1 ; 2 ) và B ( 3 ; - 5 ; 0 ) . Tọa độ trung điểm của đoạn thẳng AB là
![]()
![]()
![]()
![]()
Trong không gian hệ tọa độ Oxyz, cho mặt phẳng (P):2x+2y-z+30 và đường thẳng (d):
x
-
1
1
y
+
3
2
z
2
. Gọi A là giao điểm của (d) và (P); gọi M là điểm thuộc (d) thỏa mãn điều kiện MA 2. Tính khoảng cách từ M đến mặt phẳng (P)? A. ...
Đọc tiếp
Trong không gian hệ tọa độ Oxyz, cho mặt phẳng (P):2x+2y-z+3=0 và đường thẳng (d): x - 1 1 = y + 3 2 = z 2 . Gọi A là giao điểm của (d) và (P); gọi M là điểm thuộc (d) thỏa mãn điều kiện MA = 2. Tính khoảng cách từ M đến mặt phẳng (P)?
A. 4 9
B. 8 3
C. 8 9
D. 2 9
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm
A
(
1
;
2
;
-
1
)
,
B
(
2
;
-
1
;
3
)
,
C
(
-
2
;
3
;
3
)
.
Tìm tọa độ điểm D là chân đường phân giác trong góc A của tam giác ABC A. D(0;3;1). B. D(0;1;3) C. D(0;-3...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A ( 1 ; 2 ; - 1 ) , B ( 2 ; - 1 ; 3 ) , C ( - 2 ; 3 ; 3 ) . Tìm tọa độ điểm D là chân đường phân giác trong góc A của tam giác ABC
A. D(0;3;1).
B. D(0;1;3)
C. D(0;-3;1).
D. D(0;3;-1).
Chọn B.
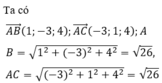
Suy ra, tam giác ABC cân ở A nên D là trung điểm BC.
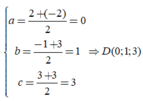
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm
A
(
1
;
2
;
-
1
)
,
B
(
2
;
-
1
;
3
)
,
C
(
-
2
;
3
;
3
)
.
Tìm tọa độ điểm D là chân đường phân giác trong góc A của tam giác ABC A. D(0;3;1) B. D(0;1;3) C. D(0;-3;1...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A ( 1 ; 2 ; - 1 ) , B ( 2 ; - 1 ; 3 ) , C ( - 2 ; 3 ; 3 ) . Tìm tọa độ điểm D là chân đường phân giác trong góc A của tam giác ABC
A. D(0;3;1)
B. D(0;1;3)
C. D(0;-3;1)
D. D(0;3;-1)
Chọn B.
Ta có
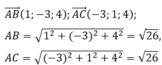
Suy ra, tam giác ABC cân ở A nên D là trung điểm BC.
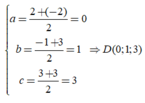
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) đi qua điểm A(2;-2;5) và tiếp xúc với các mặt phẳng
(
α
)
:
x
1
,
(
β
)
:
y
-
1
,
(
γ
)
:
z
1
. Bán kính của mặt cầu (S) bằng A.
33
B. 1 C.
3...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) đi qua điểm A(2;-2;5) và tiếp xúc với các mặt phẳng ( α ) : x = 1 , ( β ) : y = - 1 , ( γ ) : z = 1 . Bán kính của mặt cầu (S) bằng
A. 33
B. 1
C. 3 2
D. 3
Trong không gian với hệ trục tọa độ Oxyz cho hai điểm
A
(
2
;
3
;
2
)
,
B
(
-
2
;
-
1
;
4
)
. Tìm tọa độ điểm E thuộc trục Oz sao cho E cách đều hai điểm A, B
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho hai điểm A ( 2 ; 3 ; 2 ) , B ( - 2 ; - 1 ; 4 ) . Tìm tọa độ điểm E thuộc trục Oz sao cho E cách đều hai điểm A, B
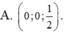
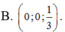
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho các điểm A (2;0;0), B (0;3;0), C (0;0;6), D (1;1;1). Có tất cả bao nhiêu mặt phẳng phân biệt đi qua 3 trong 5 điểm O, A, B, C, D? A. 6 B. 10 C. 7 D. 5.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho các điểm A (2;0;0), B (0;3;0), C (0;0;6), D (1;1;1). Có tất cả bao nhiêu mặt phẳng phân biệt đi qua 3 trong 5 điểm O, A, B, C, D?
A. 6
B. 10
C. 7
D. 5.
Chọn C
Phương trình mặt phẳng 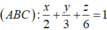
Ta thấy 4 điểm A, B, C, D đồng phẳng (do D ∈ (ABC)).
Chọn 3 trong 5 điểm có ![]()
Chọn 3 trong 4 điểm đồng phẳng A, B, C, D có ![]()
Vậy có 10 - 4 + 1 = 7 => mặt phẳng phân biệt đi qua 5 điểm đã cho.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) có phương trình: 3x+4y+2z+40 và điểm A(1;-2;3). Tính khoảng cách d từ A đến (P) A.
d
5
9
B.
d
5
29
C.
d
5
29
D. ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) có phương trình: 3x+4y+2z+4=0 và điểm A(1;-2;3). Tính khoảng cách d từ A đến (P)
A. d = 5 9
B. d = 5 29
C. d = 5 29
D. 5 3