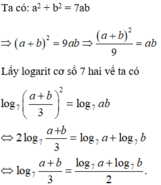Ta có : \(a^2+b^2\ge ab+1\)

\(2\sqrt{a^2b^2}\ge ab+1\)

\(ab\ge1\)

Dấu = xảy ra \(< =>a=b=\sqrt{1}=1\)

Bđt ngược dấu rồi thì phải

Nếu \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge1\)(1)

<=> \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)(Vì a + b + c = 9)

<=> \(1+\frac{a}{b}+\frac{a}{c}+\frac{b}{a}+1+\frac{b}{c}+\frac{c}{a}+\frac{c}{b}+1\ge9\) 

<=> \(\left(\frac{a}{b}+\frac{b}{a}\right)+\left(\frac{a}{c}+\frac{c}{a}\right)+\left(\frac{b}{c}+\frac{c}{b}\right)\ge6\)

Lại có \(\frac{a}{b}+\frac{b}{a}\ge2\)

<=>  \(\frac{a^2+b^2}{ab}\ge2\Leftrightarrow a^2+b^2\ge2ab\Leftrightarrow\left(a-b\right)^2\ge0\left(\text{đúng}\right)\)

Tương tự \(\hept{\begin{cases}\frac{a}{c}+\frac{c}{a}\ge2\\\frac{b}{c}+\frac{c}{b}\ge2\end{cases}}\)

<=> \(\left(\frac{a}{b}+\frac{b}{a}\right)+\left(\frac{a}{c}+\frac{c}{a}\right)+\left(\frac{b}{c}+\frac{c}{b}\right)\ge6\)(đúng) 

=> (1) được chứng minh

Áp dụng bđt Svac-xơ ta có \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge\frac{\left(1+1+1\right)^2}{a+b+c}=\frac{9}{a+b+c}=\frac{9}{9}=1\) ( Vì a+b+c=1)

\(a+b=1\Leftrightarrow b=1-a\\ \Leftrightarrow P=a^2+1-a=\left(a-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\\ P_{min}=\dfrac{3}{4}\Leftrightarrow a=\dfrac{1}{2}\Leftrightarrow b=\dfrac{1}{2}\)

Chọn B

Từ \(\frac{1}{a}+\frac{1}{b}=2\Rightarrow\frac{a}{ab}+\frac{b}{ab}=2\Rightarrow\frac{a+b}{ab}=2\)

\(\Rightarrow2ab=a+b\ge2\sqrt{ab}\Rightarrow\hept{\begin{cases}ab\ge1\\a+b\ge2\sqrt{ab}\ge2\end{cases}}\)

Áp dụng BĐT AM-GM ta có:

\(a^4+b^2+2ab^2\ge2\sqrt{a^4b^2}+2ab^2=2a^2b+2ab^2\)

\(b^4+a^2+2a^2b\ge2\sqrt{a^2b^4}+2a^2b=2ab^2+2a^2b\)

Khi đó \(Q\le\frac{1}{2a^2b+2ab^2}+\frac{1}{2ab^2+2a^2b}\le\frac{1}{4}+\frac{1}{4}=\frac{1}{2}\)

Đẳng thức xảy ra khi \(a=b=1\)

P/s: 2ab -> 2a²b và 2ab²

Đặt: \(k=\frac{a^2+b^2}{ab+1}\) , \(k\in Z\)

Giả sử, k không là số chính phương. 

Cố định số nguyên dương kk, sẽ tồn tại cặp (a,b)(a,b) . Ta kí hiệu 

\(S=a,b\in NxN\)| \(\frac{a^2+b^2}{ab+1}=k\)

Theo nguyên lí cực hạn thì các cặp thuộc SS tồn tại (A,B)(A,B) sao cho A+B đạt min 

Giả sử: \(A\ge B>0\). Cố định B ta còn số A thảo phương trình \(k=\frac{x+B^2}{xB+1}\)

\(\Leftrightarrow x^2-kBx+B^2-k=0\)phương trình có nghiệm là A.

Theo Viet: \(\hept{\begin{cases}A+x_2=kB\\A.x_2=B^2-k\end{cases}}\)

Suy ra: \(x_2=kB-A=\frac{B^2-k}{A}\)

Dễ thấy x₂ nguyên.

Nếu x₂ < 0 thì \(x_2^2-kBx_2+B^2-k\ge x_2^2+k+B^2-k>0\) vô lý. Suy ra: _{\(x_2\ge0\)} do đó \(x_2,B\in S\)

Do: \(A\ge B>0\Rightarrow x_2=\frac{B^2-k}{A}< \frac{A^2-k}{A}< A\)

Suy ra: \(x_2+B< A+B\) (trái với giả sử A+BA+B đạt min) 

Suy ra kk là số bình phương

\(2.\left(a^2+b^2\right)-1⋮a+b+1\left(a+b+1\in Z\right)\)

\(\Leftrightarrow2a^2+2b^2-1⋮a+b+1\Leftrightarrow\left(2b\right)^2-1^2⋮a+b+1\)

\(\Leftrightarrow\left(2b-1\right).\left(2b+1\right)⋮2b+1\left(\text{luôn đúng}\right)\)

p/s: ko bt cách c/m này đc ko nx...

thế còn việc chưng minh a=b ?

tớ làm theo cách nếu a=b <=> 2.(a²+b²)-1 chia hết cho a+b+1