Cho hình vuông MNPQ , lấy điểm E thuộc cạnh MQ , điểm F thuộc cạnh NP sao cho ME = PF . Các đường thẳng MF và NE cắt đường thẳng PQ lần lượt tại C và B . Kéo dài MB ; NC cắt nhau tại A . CMR : tam giác abc là tam giác vuông

Những câu hỏi liên quan
Cho hình vuông MNPQ , lấy điểm E thuộc cạnh MQ , điểm F thuộc cạnh NP sao cho ME = PF . Các đường thẳng MF và NE cắt đường thẳng PQ lần lượt tại C và B . Kéo dài MB ; NC cắt nhau tại A . CMR : tam giác abc là tam giác vuông
Gợi ý thôi cx được nhưng mà gợi ý theo kiểu chi tiết nhé , đừng bảo là kẻ cái này cái nọ rồi tự giải thì mik chịu :D
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình vuông MNPQ cạnh a (với a>0), điểm E thuộc cạnh NP, điểm F thuộc cạnh MQ sao cho PE=MF. Các đường thẳng ME, NF cắt đường thẳng PQ theo thứ tự tại C, B.
a) Chứng minh rằng PC.BQ=a^2
b) Chứng minh rằng BM vuông góc với CN
c) Các điểm E, F ở vị trí nào thì BC có độ dài nhỏ nhất
Cho hình vuông MNPQ cạnh a (với a>0), điểm E thuộc cạnh Np, điểm F thuộc cạnh MQ sao cho PE=MF . các đường thẳng ME, NF cắt đường thẳng PQ theo thứ tự tại C, B.
a. Chứng minh rằng PC.BQ=a2
b. Chứng minh rằng BM vuông góc với CN
c Các điểm E,F ở vị trí nào thì BC có độ dài nhỏ nhất
Cho tứ giác MNPQ nội tiếp đường tròn đường kính MQ. Hai đường chéo MP và NQ cắt nhau tại E. Gọi F là điểm thuộc đường thẳng MQ sao cho EF vuông góc với MQ. Đường thẳng PF cắt đường tròn đường kính MQ tại điểm thứ 2 là K. Gọi L là giao điểm của NQ và PF. Chứng minh rằng: NQ.LE = NE.LQ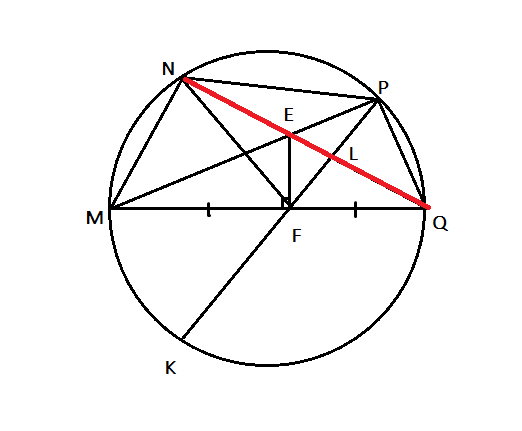
Cho tam giác MNP có MN=MP, gọi I là trung điểm của NP.
a/ trên cạnh MP, MN lần lượt lấy điểm E,F sao cho ME=MF. Chứng minh: NE=PF.
b/ Gọi H là giao điểm của NE và PF. Chứng minh: M,H,I thẳng hàng.
c/ Chứng minh EF//NP
Cho tứ giác MNPQ nội tiếp (O) đường kính MQ, hai đường chéo MF và NQ cắt nhau tại E .Gọi F là điểm thuộc MQ sao cho EF vuông góc với MQ .Đường thẳng PF cắt (O) tại điểm thứ 2 là K. OQ và PF cắt nhau tại L . cmr :
a, tứ giác QEFP nội tiếp
b, FM là tia phân giác của góc NFK
c, EN.QL=QL.EL
Em cần gấp với ah ! Cho hình vuông MNPQ, điểm A bất kỳ trên cạnh NP. Qua M vẽ đường thẳng vuông góc với MA cắt PQ và PN lần lượt tại B và C a, C/m tam giác MAB cân b, C/m MB^2= BQ.A c, Cho MN=15cm, AN=8cm. Tính CN,CM
a: Xét ΔMNA vuông tại N và ΔMQB vuông tại Q có
MN=MQ
góc NMA=góc QMB
=>ΔMNA=ΔMQB
=>MA=MB
=>ΔMAB cân tại M
c: NC=15^2/8=225/8(cm)
CM=căn 225/8*289/8=255/8(cm)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Trên cạnh AB lần lượt lấy các điểm M và E sao cho AM = ME = EB. Gọi N là trung điểm của CD. Điểm G thuộc NE thỏa mãn
EG =1/3EN. Đường thẳng AG cắt các đường thẳng BC, DC theo thứ tự ở I và P.
a) Biết AB = 5 cm. Tính CP?
b) Tính tỉ số IB/IC
c)Gọi K là trung điểm của NP. Chứng minh M, G, K thẳng hàng?
Cho tam giác ABC cân tại A. Lấy điểm E thuộc cạnh BC, điểm F thuộc tia đối của tia CB sao cho BE CF. Qua E kẻ đường thẳng vuông góc với BC cắt cạnh AB tại M. Qua F kẻ đường thẳng vuông góc với BC cắt cạnh AC kéo dài tại N.a, Cho BM 10 cm, BE 6 cm. Tính EMb, Cho góc ACB 40 độ. So sánh các cạnh của tam giác ABCc, Chứng minh : EM FNd, Gọi H là giao điểm của BC và MN. Chứng minh H là trung điểm của EFe, Chứng minh : CM CNf, Vẽ đường thẳng qua A và song song EM và cắt BC tại I. Vẽ đường thẳng B...
Đọc tiếp
Cho tam giác ABC cân tại A. Lấy điểm E thuộc cạnh BC, điểm F thuộc tia đối của tia CB sao cho BE = CF. Qua E kẻ đường thẳng vuông góc với BC cắt cạnh AB tại M. Qua F kẻ đường thẳng vuông góc với BC cắt cạnh AC kéo dài tại N.
a, Cho BM = 10 cm, BE = 6 cm. Tính EM
b, Cho góc ACB = 40 độ. So sánh các cạnh của tam giác ABC
c, Chứng minh : EM = FN
d, Gọi H là giao điểm của BC và MN. Chứng minh H là trung điểm của EF
e, Chứng minh : CM > CN
f, Vẽ đường thẳng qua A và song song EM và cắt BC tại I. Vẽ đường thẳng Bx vuông góc vs AB tại B, đường thẳng Cy vuông góc với AC tại C. Chứng minh ba đường thẳng : AI, bx, Cy cùng đi qua một điểm
Mọi người làm hộ e vs ạ, vẽ hình luôn nhé, câu a,b,c ko làm cx đc, mai e phải nộp rồi. SOS ,












