Các câu hỏi tương tự
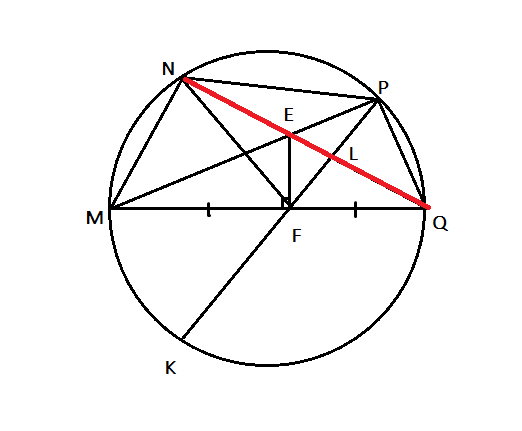
Cho tứ giác MNPQ nội tiếp (O) đường kính MQ, hai đường chéo MF và NQ cắt nhau tại E .Gọi F là điểm thuộc MQ sao cho EF vuông góc với MQ .Đường thẳng PF cắt (O) tại điểm thứ 2 là K. OQ và PF cắt nhau tại L . cmr :
a, tứ giác QEFP nội tiếp
b, FM là tia phân giác của góc NFK
c, EN.QL=QL.EL
Cho tam giác MNQ vuông tại M có MNMQ và MNQ60 độME là phân giác của góc NMQ (E thuộc NQ)Vẽ đường thẳng qua E và vuông góc với đường thẳng NQ cắt MQ tại H, cắt đường thẳng MN tại F. Gọi O là tâm đường tròn ngoại tiếp tam giác NFQ.a) C/M: Tứ giác FMEQ nội tiếp trong một đường tròn. Xác định vị trí tâm I của đường tròn đó.b) C/M: OE//NHgiúp mình với ạ. Các bạn vẽ hình cho mình với nhé
Đọc tiếp
Cho tam giác MNQ vuông tại M có MN<MQ và MNQ=60 độ
ME là phân giác của góc NMQ (E thuộc NQ)
Vẽ đường thẳng qua E và vuông góc với đường thẳng NQ cắt MQ tại H, cắt đường thẳng MN tại F. Gọi O là tâm đường tròn ngoại tiếp tam giác NFQ.
a) C/M: Tứ giác FMEQ nội tiếp trong một đường tròn. Xác định vị trí tâm I của đường tròn đó.
b) C/M: OE//NH
giúp mình với ạ. Các bạn vẽ hình cho mình với nhé
Cho đường tròn (O;R),đường kính AB.Gọi M là một điểm thuộc đường tròn sao cho MAMB.Đường thẳng vuông góc với AB tại A cắt tiếp tuyến M của đường tròn (O) tại điểm E .Kẻ MP vuông góc với AB(P thuộc AB);MQ vuông góc với AE(Q thuộc AB)1,Chứng minh:Tứ giác AEMO là tứ giác nội tiếp.2,Gọi I là trung điểm của PQ,Chứng minh:Tứ giác AQMP là hình chữ nhật,từ đó chứng minh ba điểm O,I,E thẳng hàng3,Gọi K là giao điểm của EB và MP.Chứng minh :OAMPAEBP
Đọc tiếp
Cho đường tròn (O;R),đường kính AB.Gọi M là một điểm thuộc đường tròn sao cho MA>MB.Đường thẳng vuông góc với AB tại A cắt tiếp tuyến M của đường tròn (O) tại điểm E .Kẻ MP vuông góc với AB(P thuộc AB);MQ vuông góc với AE(Q thuộc AB)
1,Chứng minh:Tứ giác AEMO là tứ giác nội tiếp.
2,Gọi I là trung điểm của PQ,Chứng minh:Tứ giác AQMP là hình chữ nhật,từ đó chứng minh ba điểm O,I,E thẳng hàng
3,Gọi K là giao điểm của EB và MP.Chứng minh :OAMP=AEBP
cho đường tròn (o) đường kính AB và đường thẳng d là tiếp tuyến của đường tròn kẻ từ B. trên d lấy hai điểm nằm khác phía với điểm B và BCBD.AC cắt (o) tại E, AD cắt (o) tại F.(E,F khác A) đường thẳng kẻ qua A vuông góc với EF cắt CD tại M.a) chứng minh tứ giác CEFD nội tiếp.b) Gọi I là tâm đường tròn ngoại tiếp tứ giác CEFD. chứng minh IM vuông góc với CD.c) gọi P là giao điểm của FE và CD. PA cắt đường tròn (o) tại K (K khác A) c/m K,B,I thẳng hàng
Đọc tiếp
cho đường tròn (o) đường kính AB và đường thẳng d là tiếp tuyến của đường tròn kẻ từ B. trên d lấy hai điểm nằm khác phía với điểm B và BC<BD.AC cắt (o) tại E, AD cắt (o) tại F.(E,F khác A) đường thẳng kẻ qua A vuông góc với EF cắt CD tại M.
a) chứng minh tứ giác CEFD nội tiếp.
b) Gọi I là tâm đường tròn ngoại tiếp tứ giác CEFD. chứng minh IM vuông góc với CD.
c) gọi P là giao điểm của FE và CD. PA cắt đường tròn (o) tại K (K khác A) c/m K,B,I thẳng hàng
Cho tứ giác MNPQ nội tiếp nửa đường tròn đk MQ. Gọi I là giao điểm của MP với NQ. Kẻ IH vuông góc với MQ
a)Cm MNIH;PQHI là tứ giác nội tiếp
b) cm NQ la pg của góc PNH
c) Gọi K là trung điểm của IQ.cm PNKH nội tiếp
d) Cm MN,PQ,IH đồng quy
Cho tam giác ABC nội tiếp đường tròn (O). Các đường cao AD,BE,CF cắt nhau tại H. Gọi I,J,M lần lượt là trung điểm của AH,EF,BC. P,Q lần lượt là các giao điểm của EF với các tiếp tuyến tại B và C của đường tròn (O). MF cắt AD tại L. ME cắt đường thẳng qua F và song song với BC tại Ka, Chứng minh MP//CF, MQ//BE.b, Chứng minh IJ luôn đi qua điểm cố định khi (O) và BC cố định, A di động trên cung BC.c, Tính góc giữa 2 đường thẳng IK và EL
Đọc tiếp
Cho tam giác ABC nội tiếp đường tròn (O). Các đường cao AD,BE,CF cắt nhau tại H. Gọi I,J,M lần lượt là trung điểm của AH,EF,BC. P,Q lần lượt là các giao điểm của EF với các tiếp tuyến tại B và C của đường tròn (O). MF cắt AD tại L. ME cắt đường thẳng qua F và song song với BC tại K
a, Chứng minh MP//CF, MQ//BE.
b, Chứng minh IJ luôn đi qua điểm cố định khi (O) và BC cố định, A di động trên cung BC.
c, Tính góc giữa 2 đường thẳng IK và EL
Cho đường tròn O đường kính A 2r Gọi M là điểm trên đường tròn khác A và B b t là giao điểm của hai tiếp tuyến của đường tròn tâm A và M hạ MP vuông góc AB và MQ vuông góc AC Gọi I là trung điểm PQ1. Chứng minh tam giác AIO vuông tại I2.Chứng minh tia MA là phân giác3. chứng minh tam giác AIQ đồng dạng vs tam giác ATM và tam giác AIP đồng dạng vs tam giác AOM4.chứng minh AO.AP2AI^2
Đọc tiếp
Cho đường tròn O đường kính A = 2r Gọi M là điểm trên đường tròn khác A và B b t là giao điểm của hai tiếp tuyến của đường tròn tâm A và M hạ MP vuông góc AB và MQ vuông góc AC Gọi I là trung điểm PQ
1. Chứng minh tam giác AIO vuông tại I
2.Chứng minh tia MA là phân giác
3. chứng minh tam giác AIQ đồng dạng vs tam giác ATM và tam giác AIP đồng dạng vs tam giác AOM
4.chứng minh AO.AP=2AI^2
Đg kính =2R.M là 1 điểm tùy ý thuộc (0) và khác A,B Các tiếp tuyến đường tròn tại A và M cắt nhau tại E MP vuông AB tại P, MQ vuông AE tại Q 1: AEMO là tứ giác nội tiếp và AQMP là hcn 2: Gọi I là trung điểm của PQ.Cm O,I,E thẳng hàng 3: gọi K là giao điểm của EP và MP. Cm tam giác AEO đồng dạng vs tam giác PMB từ đó suy ra K là trung điểm của MP
cho tam giác ABC có ba góc nhọn .Đường tròn tâm O đường kính BC cắt AB, AC lần lượt tại E và D. gọi giao điểm của CE và BD là H
a) chứng minh tứ giác AEHD nội tiếp
b) kẻ AF vuông góc với BC tại F. Chứng minh A, H, F thẳng hàng
c) đường thẳng EF cắt đường tròn tại điểm thứ 2 là K. chứng minh DK// AF