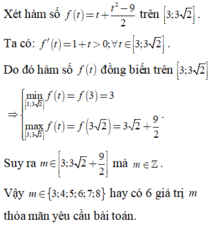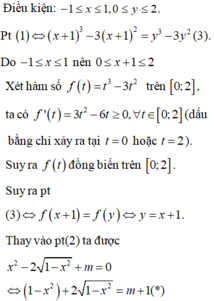tìm nghiệm nguyên của phương trình 7x2+ 3y2 = 714

Những câu hỏi liên quan
tìm nghiệm nguyên của phương trình
x2+3y2+2xy−18(x+y)+73=0x2+3y2+2xy−18(x+y)+73=0
tìm nghiệm nguyên của phương trình 7x2+ 3y2 = 714
Ta có:\(7⋮7\Rightarrow7x^2⋮7;714⋮7\)
\(\Rightarrow3y^2⋮7\)
Mà \(\left(3,7\right)=1\Rightarrow y^2⋮7\Rightarrow y^2⋮49\)(tính chất số chính phương)
Lại có:\(3y^2\le714\Rightarrow y^2\le238\)
\(\Rightarrow y^2\in\left\{49;196\right\}\)vì y là số chính phương
Với \(y^2=49\Rightarrow\orbr{\begin{cases}y=7\Rightarrow x=\pm9\\y=-7\Rightarrow7x^2=567\Rightarrow x^2=81\Rightarrow x=\pm9\end{cases}}\)
tương tự với \(y^2=196\)nhé
Đúng 0
Bình luận (0)
akk!về cái tính chất số chính phương thì được phát biểu như thế này:
Số chính phương khi chia hết cho số nguyên tố p thì chia hết cho p bình phương.
Đúng 0
Bình luận (0)
giải phương trình nghiệm nguyên : 2x2 + 5xy + 3y2 = 0
\(2x^2+5xy+3y^2\\= 2x^2+2xy+3xy+3y^2\\= 2x\left(x+y\right)+3y\left(x+y\right)\\=\left(2x+3y\right)\left(x+y\right) \)
Đúng 2
Bình luận (0)
2x^2-5xy-3y^2
= 2^x + xy - 6xy - 3y^2
= x(2x + y) - 3y(2x + y)
= (2x + y)(x - 3y)
Đúng 2
Bình luận (0)
Giải phương trình nghiệm nguyên sau:
6.(6x2 + 3y2 + z2) = 5t2
Giải phương trình nghiệm nguyên: x2+3y2+4xy-2x-6y=5
\(\Leftrightarrow x^2+3xy+3y^2+xy-2x-6y=5\)
\(\Leftrightarrow x\left(x+3y\right)+y\left(x+3y\right)-2\left(x+3y\right)=5\)
\(\Leftrightarrow\left(x+y-2\right)\left(x+3y\right)=5\)
Bảng giá trị:
| x+y-2 | -5 | -1 | 1 | 5 |
| x+3y | -1 | -5 | 5 | 1 |
| x | -4 | 4 | 2 | 10 |
| y | 1 | -3 | 1 | -3 |
Vậy \(\left(x;y\right)=\left(-4;1\right);\left(4;-3\right);\left(2;1\right);\left(10;-3\right)\)
Đúng 1
Bình luận (0)
Tính
Δ
và tìm số nghiệm của phương trình
7
x
2
-
12
x
+
4
0
A.
Δ
6 và phương trình có hai nghiệm phân biệt B.
Δ
8 và phương trình có hai nghiệm phân biệt C.
Δ
8 và phương trình có nghiệm kép D.
Δ
0 và phương trình có hai nghiệm phân biệt
Đọc tiếp
Tính Δ ' và tìm số nghiệm của phương trình 7 x 2 - 12 x + 4 = 0
A. Δ ' = 6 và phương trình có hai nghiệm phân biệt
B. Δ ' = 8 và phương trình có hai nghiệm phân biệt
C. Δ ' = 8 và phương trình có nghiệm kép
D. Δ ' = 0 và phương trình có hai nghiệm phân biệt
Đáp án B
Phương trình 7 x 2 - 12 x + 4 = 0 có a = 7; b' = -6; c = 4 suy ra:
Δ ' = ( b ' ) 2 - a c = ( - 6 ) 2 - 4 . 7 = 8 > 0
Nên phương trình có hai nghiệm phân biệt.
Đúng 0
Bình luận (0)
Tính
Δ
và tìm số nghiệm của phương trình
7
x
2
−
12
x
+
4
0
A.
Δ
6 và phương trình có hai nghiệm phân biệt B.
Δ
8 và phương trình có hai nghiệm phân biệt C.
Δ
8 và phương trình có nghiệm kép D.
Δ
0 và phương trình có hai nghiệm phân biệt
Đọc tiếp
Tính Δ ' và tìm số nghiệm của phương trình 7 x 2 − 12 x + 4 = 0
A. Δ ' = 6 và phương trình có hai nghiệm phân biệt
B. Δ ' = 8 và phương trình có hai nghiệm phân biệt
C. Δ ' = 8 và phương trình có nghiệm kép
D. Δ ' = 0 và phương trình có hai nghiệm phân biệt
Phương trình 7x2 − 12x + 4 = 0
có a = 7;b’ = −6; c = 4 suy ra
Δ ' = b ' 2 − a c = (−6)2 – 4.7 = 8 > 0
Nên phương trình có hai nghiệm phân biệt
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m để phương trình
1
+
x
+
8
-
x
+
8
+
7
x
-
7
x
2
m...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình 1 + x + 8 - x + 8 + 7 x - 7 x 2 = m có nghiệm thực?
A. 13.
B. 12.
C. 6.
D. 7.
Hỏi có bao nhiêu giá trị nguyên của m để hệ phương trình sau có nghiệm:
x
3
-
y
3
+
3
y
2
-
3
x
-
2...
Đọc tiếp
Hỏi có bao nhiêu giá trị nguyên của m để hệ phương trình sau có nghiệm:
x 3 - y 3 + 3 y 2 - 3 x - 2 = 0 1 x 2 + 1 - x 2 - 3 2 y - y 2 + m = 0 2
A. 1
B. 3
C. 2
D. 4
Cho phương trình 7x2 + 2(m – 1)x - m2 = 0
Trong trường hợp phương trình có nghiệm, dùng hệ thức Vi-ét, hãy tính tổng các bình phương hai nghiệm của phương trình theo m.
Gọi hai nghiệm của phương trình là x1; x2.
Theo định lý Vi-et ta có: 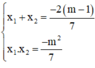
Khi đó:
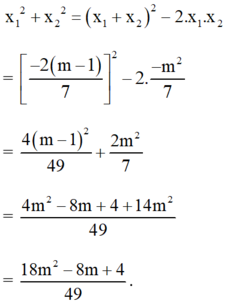
Đúng 0
Bình luận (0)