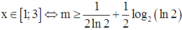tìm nghiệm nguyên của phương trình 12x2 +26xy +15y2=4671
tìm nghiệm nguyên của phương trình 12x2 + 26xy + 15y2 = 4671
Tìm số nghiệm nguyên của bất phương trình 1 2 x 2 - x - 12 > 1 2 x - 1
A. 7
B. 9
C. 8
D. 10
Hệ phương trình x 2 - 2 x y + 3 y 2 = 9 2 x 2 - 13 x y + 15 y 2 = 0 có nghiệm là?
A. (3; 1); (−3; −1)
B. 5 2 2 ; 2 2 ; - 5 2 2 ; - 2 2
C. (3; 1); (−3; −1); 5 2 2 ; 2 2 ; - 5 2 2 ; - 2 2
D. (3; −1); (−3; 1); 5 2 2 ; 2 2 ; - 5 2 2 ; - 2 2
Bất phương trình 1 2 x 2 + 4 x ≥ 1 32 có bao nhiêu nghiệm nguyên?
A.. 6
B. 7
C. 5
D. 4
Cho phương trình 1 2 x 2 - 2 x + 1 = 0
Vẽ các đồ thị của hai hàm số y = 1 2 x 2 , y = 2x – 1 trong cùng một mặt phẳng tọa độ. Dùng đồ thị tìm giá trị gần đúng nghiệm của phương trình (làm tròn đến chữ số thập phân thứ hai)
*Vẽ đồ thị hàm số y = 1 2 x 2
| x | -2 | -1 | 0 | 1 | 2 |
| y = 1 2 x 2 | 2 | 1/2 | 0 | 1/2 | 2 |
*Vẽ đồ thị hàm số y = 2x – 1
Cho x = 0 thì y = -1 ⇒ (0; -1)
Cho y = 0 thì x = 1/2 ⇒ (1/2 ; 0)
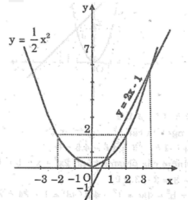
Dựa vào đồ thị, ta có : x 1 ≈ 0 , 60 , x 2 ≈ 3 , 40
Tìm các giá trị của tham số m để phương trình 1 2 x 2 − 4 x + 3 = m 2 có 3 nghiệm phân biệt
A. m = 3
B. − 3 < m < 3
C. m = ± 3
D. Không tồn tại
Giải bất phương trình 1 2 x 2 > 2 x . Gọi tập nghiệm là S. Tìm S.
A. (-1;0)
B. 0 ; + ∞
C. (0;1)
D. Rỗng
Tìm tập hợp các giá trị thực của m sao cho bất phương trình log 2 x + m ≥ 1 2 x 2 có nghiệm x ∈ 1 ; 3
A. 1 ln 2 ; + ∞
B. 9 2 − log 2 3 ; + ∞
C. 1 2 ; + ∞
D. 1 ln 2 + 1 2 log 2 ln 2 ; + ∞
Đáp án D
Bất phương trình
log 2 x + m ≥ 1 2 x 2 ⇔ m ≥ 1 2 x 2 − log 2 x * .
Xét hàm số f x = 1 2 x 2 − log 2 x với x ∈ 1 ; 3 ,
ta có f ' x = x − 1 x . ln 2 = x 2 . ln 2 − 1 x . ln 2 .
Phương trình
f ' x = 0 ⇔ x 2 . ln 2 − 1 = 0 ⇔ x 2 = 1 ln 2 ⇔ x = 1 ln 2 .
Tính các giá trị
f 1 = 1 2 ; f 1 ln 2 = 1 2 ln 2 + 1 2 log 2 ln 2 ; f 3 = 9 2 − log 2 3.
Dựa vào BBT, suy ra giá trị nhỏ nhất của hàm số f(x) là
f 1 ln 2 = 1 2 ln 2 + 1 2 log 2 ln 2 .
Khi đó, bất phương trình (*) có nghiệm
x ∈ 1 ; 3 ⇔ m ≥ 1 2 ln 2 + 1 2 log 2 ln 2 .
Tìm tập hợp các giá trị thực của m sao cho bất phương trình log2x + m ≥ 1 2 x 2 có nghiệm x ∈ 1 ; 3
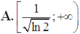
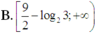
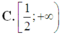
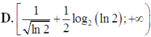
Đáp án D
Bất phương trình
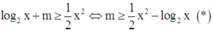
Xét hàm số
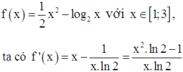
Phương trình
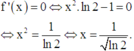
Tính các giá trị
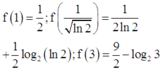
Dựa vào BBT, suy ra giá trị nhỏ nhất của hàm số f(x) là
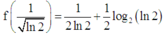
Khi đó, bất phương trình (*) có nghiệm