Bài 19 Cho tứ giác ABCD có Â = 800. Tổng số đo các góc ngoài đỉnh B, C, D bằng:
Những câu hỏi liên quan
Cho tứ giác ABCD có A ^ = 100 ° . Tổng số đo các góc ngoài đỉnh B, C, D bằng:
A. 180 °
B. 260 °
C. 280 °
D. 270 °
Đáp án cần chọn là: C
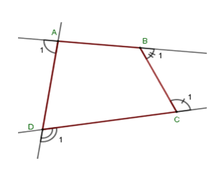
Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là A 1 ^ ; B 1 ^ ; C 1 ^ ; D 1 ^ .
Khi đó ta có :
A ^ + A 1 ^ = 180 ° ⇒ A 1 ^ = 180 ° - A ^ ;
Theo kết quả các câu trước ta có
A 1 ^ + B 1 ^ + C 1 ^ + D 1 ^ = 360 ° ⇒ B 1 ^ + C 1 ^ + D 1 ^ = 360 ° - A ^ = 360 ° - 80 ° = 280 °
Vậy B 1 ^ + C 1 ^ + D 1 ^ = 280 °
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có A ^ = 80 ° . Tổng số đo các góc ngoài đỉnh B, C, D bằng:
A. 180 °
B. 260 °
C. 280 °
D. 270 °
Đáp án cần chọn là: B
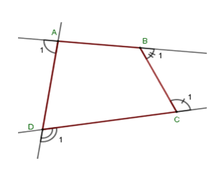
Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là A 1 ^ ; B 1 ^ ; C 1 ^ ; D 1 ^ .
Khi đó ta có :
A ^ + A 1 ^ = 180 ° ⇒ A 1 ^ = 180 ° - A ^ ;
Theo kết quả các câu trước ta có
A 1 ^ + B 1 ^ + C 1 ^ + D 1 ^ = 360 ° ⇒ B 1 ^ + C 1 ^ + D 1 ^ = 360 ° - A ^ = 360 ° - 100 ° = 260 °
Vậy B 1 ^ + C 1 ^ + D 1 ^ = 260 °
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có tổng số đo góc ngoài tại hai đỉnh B và C là 200 ° . Tổng số đo các góc ngoài tại 2 đỉnh A, C là:
A. 160 °
B. 260 °
C. 180 °
D. 100 °
Đáp án cần chọn là: A
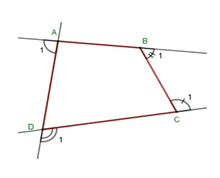
Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là A 1 ^ ; B 1 ^ ; C 1 ^ ; D 1 ^ .
Khi đó ta có :
A ^ + A 1 ^ = 180 ° ⇒ A 1 ^ = 180 ° - A ^ ; B ^ + B 1 ^ = 180 ° ⇒ B 1 ^ = 180 ° - B ^ ; C ^ + C 1 ^ = 180 ° ⇒ C 1 ^ = 180 ° - C ^ ; D ^ + D 1 ^ = 180 ° ⇒ D 1 ^ = 180 ° - D ^ ;
Suy ra
A 1 ^ + B 1 ^ + C 1 ^ + D 1 ^ = 180 ° - A ^ + 180 ° - B ^ + 180 ° - C ^ + 180 ° - D ^ = 720 ° - A ^ + B ^ + C ^ + D ^ = 720 ° - 360 ° = 360 °
Vậy tổng số đo các góc ngoài tại 4 đỉnh A, B, C, D là 360 ° .
Mà tổng số đo góc ngoài tại hai đỉnh B, C bằng 200 ° nên tổng số đo góc ngoài tại hai đỉnh A, D bằng 360 ° - 200 ° = 160 °
Đúng 0
Bình luận (0)
Cho tứ giác ABCD. Tổng số đo các góc ngoài tại 4 đỉnh A, B, C, D là:
A. 300 °
B. 270 °
C. 180 °
D. 360 °
Đáp án cần chọn là: D
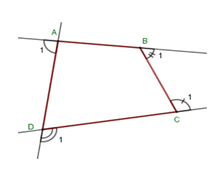
Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là A 1 ^ ; B 1 ^ ; C 1 ^ ; D 1 ^ .
Khi đó ta có :
A ^ + A 1 ^ = 180 ° ⇒ A 1 ^ = 180 ° - A ^ ; B ^ + B 1 ^ = 180 ° ⇒ B 1 ^ = 180 ° - B ^ ; C ^ + C 1 ^ = 180 ° ⇒ C 1 ^ = 180 ° - C ^ ; D ^ + D 1 ^ = 180 ° ⇒ D 1 ^ = 180 ° - D ^ ;
Suy ra
A 1 ^ + B 1 ^ + C 1 ^ + D 1 ^ = 180 ° - A ^ + 180 ° - B ^ + 180 ° - C ^ + 180 ° - D ^ = 720 ° - A ^ + B ^ + C ^ + D ^ = 720 ° - 360 ° = 360 °
Vậy tổng số đo các góc ngoài tại 4 đỉnh A, B, C, D là 360 ° .
Đúng 1
Bình luận (0)
Bài 10: Cho tứ giác ABCD có A 65 ;B 117 ;C 71 . Số đo góc ngoài tại đỉnh D bằng:
A. 1130
B. 1070
C. 730
D. 830
Tứ giác ABCD có Â=65 độ,B=117độ,C=71độ . Tính số đo góc ngoài tại đỉnh D
Ta có: góc D = 360 độ - 65 độ - 117 độ - 71 độ = 107 độ
Lại có: góc ngoài tại đỉnh D là góc kề bù với góc D nên số đo góc ngoài tại đỉnh D là: 180 độ - 107 độ = 73 độ.
Chúc may mắn và nhớ k cho mình với nhoa!
Đúng 0
Bình luận (0)
SGK Toán 8 – Chân trời sáng tạo
21 tháng 7 2023 lúc 21:50
Tứ giác \(ABCD\) có góc ngoài tại đỉnh \(A\) bằng \(65^\circ \), góc ngoài tại đỉnh \(B\) bằng \(100^\circ \), góc ngoài tại đỉnh \(C\) bằng \(60^\circ \). Tính số đo góc ngoài tại đỉnh \(D\).
Số đo góc ngoài tại đỉnh \(D\) là: \(360^\circ - \left( {65^\circ + 100^\circ + 60^\circ } \right) = 135^\circ \)
Đúng 0
Bình luận (0)
Cho tứ giác ABCD. Tổng số đo các góc ngoài tại 4 đỉnh A, B, C, D là
A. 3000
B. 2700
C. 1800
D. 3600
Xem thêm câu trả lời
Cho tứ giác ABCD có
A
^
50
°
;
C
^
150
°
;
D
^
45
°
. Số đo góc ngoài tại đỉnh B bằng: A.
65
°
B.
66
°
C.
130
°
D.
115
°
Đọc tiếp
Cho tứ giác ABCD có A ^ = 50 ° ; C ^ = 150 ° ; D ^ = 45 ° . Số đo góc ngoài tại đỉnh B bằng:
A. 65 °
B. 66 °
C. 130 °
D. 115 °
Đáp án cần chọn là: A
Xét tứ giác ABCD có A ^ + B ^ + C ^ + D ^ = 360 ° (định lí)
Hay 50 ° + B ^ + 150 ° + 45 ° = 360 °
⇒ B ^ = 360 ° - 50 ° - 150 ° - 45 ° = 115 °
Nên góc ngoài tại đỉnh B có số đo là 180 ° - B ^ = 180 ° - 115 ° = 65 °
Đúng 1
Bình luận (0)