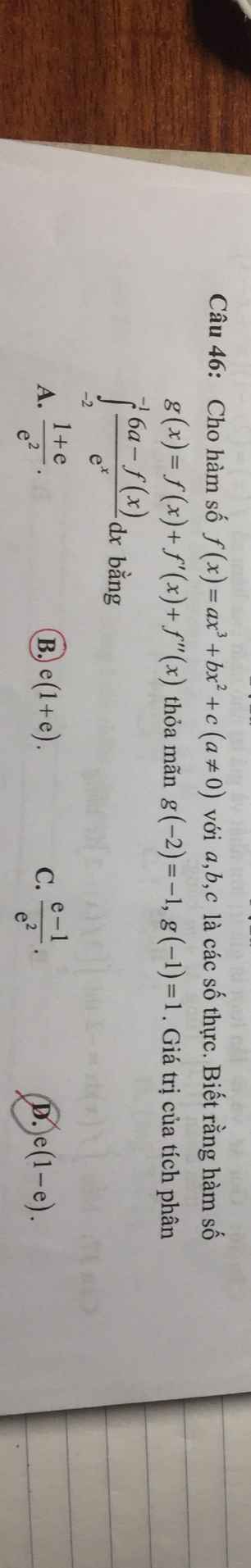tự làm là hạnh phúc của mỗi công dân.

Trắc nghiệm rất lẹ (chắc vài giây), còn tự luận hơi lâu:

Hiển nhiên chỉ cần xét với \(x>2\) (vì vế trái luôn dương). Chú ý rằng \(a^{logx}=x^{loga}\)

Với \(a=10\Rightarrow x+2=x-2\) vô nghiệm (ktm)

- Trắc nghiệm: với \(a>10\Rightarrow\left(x^{loga}+2\right)^{loga}>x+2>x-2\) pt vô nghiệm

Với \(a< 10\) chọn 2 giá trị a=2 và a=9 để kiểm tra hàm \(\left(x^{loga}+2\right)^{loga}-x+2\) thấy đều đổi dấu ở chế độ table \(\Rightarrow a=\left\{2;3;...;9\right\}\) có 8 giá trị nguyên

- Tự luận: xét với \(x>2\), đặt \(loga=m>0\) pt trở thành: \(\left(x^m+2\right)^m=x-2\)

Đặt \(x^m+2=t\Rightarrow\left\{{}\begin{matrix}x^m=t-2\\t^m=x-2\end{matrix}\right.\)

\(\Rightarrow x^m-t^m=t-x\Rightarrow x^m+x=t^m+t\) (1)

Xét hàm \(f\left(x\right)=x^m+x\Rightarrow f'\left(x\right)=mx^{m-1}+1>0\Rightarrow f\left(x\right)\) đồng biến

Do đó \(\left(1\right)\Rightarrow x=t\Rightarrow x^m=x-2\Rightarrow x^m-x+2=0\)

Xét hàm \(f\left(x\right)=x^m-x+2\)

- Với \(m>1\Rightarrow f'\left(x\right)=m.x^{m-1}-1>1-1\ge0\Rightarrow f\left(x\right)\) đồng biến

\(\Rightarrow f\left(x\right)>f\left(2\right)=2^m-2+2=2^m>0\Rightarrow f\left(x\right)\) vô nghiệm (ktm)

- Với \(0< m< 1\) ta có:

\(f\left(2\right)=2^m>0\)

\(\lim\limits_{x\rightarrow+\infty}\left(x^m-x+2\right)=\lim\limits_{x\rightarrow+\infty}x\left(x^{m-1}-1+\dfrac{2}{x}\right)\)

Chú ý rằng \(m< 1\Rightarrow x^{m-1}=\dfrac{1}{x^{1-m}}\rightarrow0\) khi \(x\rightarrow+\infty\Rightarrow x^{m-1}-1+\dfrac{2}{x}\rightarrow-1\Rightarrow\lim\limits_{x\rightarrow+\infty}\left(x^m-x+2\right)=-\infty\)

\(\Rightarrow f\left(2\right).\lim\limits_{x\rightarrow+\infty}f\left(x\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thỏa mãn \(x>2\)

Vậy \(0< m< 1\) hay \(0< loga< 1\Rightarrow2\le a< 10\Rightarrow a=\left\{2;3;...;9\right\}\)

a)Vì x,y ko âm =>x,y>0

=>ko tồn tại

b)Có vô số nghiệm x,y 

Vd:1 và 0

-2 và 3

-3 và 4

.....

Thắng Nguyễn : x,y ko âm đâu có nghĩa là x,y > 0 

Theo tớ thì có 2 cặp:

x=0  và y = 1

x=1 và y=0

Cold Wind:nhầm >= 0 :D

\(I=\int\limits^{-1}_{-2}\dfrac{6a}{e^x}dx-\int\limits^{-1}_{-2}\dfrac{f\left(x\right)}{e^x}dx=J-I_1\)

Xét \(I_1\) , đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=e^{-x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=-e^{-x}\end{matrix}\right.\)

\(\Rightarrow I_1=-f\left(x\right).e^{-x}|^{-1}_{-2}+\int\limits^{-1}_{-2}\dfrac{f'\left(x\right)}{e^x}dx=-f\left(-1\right).e+f\left(-2\right).e^2+I_2\)

Xét \(I_2\) , đặt \(\left\{{}\begin{matrix}u=f'\left(x\right)\\dv=e^{-x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f''\left(x\right)dx\\v=-e^{-x}\end{matrix}\right.\)

\(\Rightarrow I_2=-f'\left(x\right).e^{-x}|^{-1}_{-2}+\int\limits^{-1}_{-2}\dfrac{f''\left(x\right)}{e^x}dx=-f'\left(-1\right).e+f'\left(-2\right).e^2+I_3\)

Xét \(I_3\) , đặt \(\left\{{}\begin{matrix}u=f''\left(x\right)\\dv=e^{-x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'''\left(x\right)dx=6a.dx\\v=-e^{-x}\end{matrix}\right.\)

\(\Rightarrow I_3=-f''\left(x\right).e^{-x}|^{-1}_{-2}+\int\limits^{-1}_{-2}\dfrac{6a}{e^x}dx=-f''\left(-1\right).e+f''\left(-2\right).e^2+J\)

Do đó:

\(I=J+f\left(-1\right).e-f\left(-2\right).e^2+f'\left(-1\right).e-f'\left(-2\right).e^2+f''\left(-1\right).e-f''\left(-2\right).e^2-J\)

\(=e\left[f\left(-1\right)+f'\left(-1\right)+f''\left(-1\right)\right]-e^2\left[f\left(-2\right)+f'\left(-2\right)+f''\left(-2\right)\right]\)

\(=e.g\left(-1\right)-e^2.g\left(-2\right)=e+e^2=e\left(e+1\right)\)

x=0 và y = 1

x=1 và y=0 

CHÚC BẠN HỌC GIỎI

TK MÌNH NHÉ

A, 1 cặp

B, vô số cặp 

Chúc bạn học giỏi 

Tk cho mình nhé