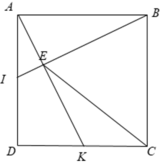
Cho hình vuông ABCD.Gọi I,K lần lượt là trung điểm của AD và DC .Gọi E là giao điểm của BI và AK . CMR CE=AB

Những câu hỏi liên quan
Cho hình vuông ABCD. Gọi I,K lần lượt là trung điểm của AD và DC. Gọi E là giao điểm của BI và AK. Chứng minh rằng CE = AB.
Cho hình vuông ABCD. Gọi I,K lần lượt là trung điểm của AD và DC. Gọi E là giao điểm của BI và AK. Chứng minh rằng CE = AB.
1: Cho hình vuông ABCD . Gọi I,K lần lượt là trung điểm của AD và DC.
a) Chứng minh rằng BI ⊥ AK.
b) Gọi E là giao điểm của BI và AK. Chứng minh rằng CE = AB.
Bài 1: Cho hình vuông ABCD. Gọi I,K lần lượt là trung điểm của AD và DC.
a) Chứng minh rằng BI ⊥ AK.
b) Gọi E là giao điểm của BI và AK. Chứng minh rằng CE = AB.
a, Vì \(\left\{{}\begin{matrix}AD=AB\\AI=DK\left(\dfrac{1}{2}AD=\dfrac{1}{2}DC\right)\\\widehat{BAD}=\widehat{ADK}=90^0\end{matrix}\right.\) nên \(\Delta AIB=\Delta DKA\left(c.g.c\right)\)
\(\Rightarrow\widehat{ABI}=\widehat{DAI}\\ \Rightarrow\widehat{DAI}+\widehat{AIB}=\widehat{ABI}+\widehat{AIB}=90^0\\ \Rightarrow BI\perp AK\)
Đúng 2
Bình luận (0)
Cho hình vuông ABCD.Gọi M;N lần lượt là trung điểm của AB và BC.Gọi K là giao điểm của CM và DN.Chứng minh AK=AD
Gọi I là trung điểm của DC. AI giao với DK tại H
+) Tứ giác AMCI là hình bình hành ( AM = CI và AM // CI) => AI // CM
+) Trong tam giác DKC có: HI // CK; I là trung điểm của DC => H là trung điểm của DK (1)
+) Xét tam giác DCN và CBM có: CN = BM ; góc DCN = CBM; DC = BC
=> tam giác DCN = CBM ( c - g - c) => góc CDN = MCB
=> góc CDN + DCM = MCB + DCM = góc DCB = 90o => góc DKC = 90o => DK vuông góc với CM
mà CM // AI => AI vuông góc với DK (2)
Từ (1)(2) => AI là đường trung trực của DK => AD = AK
Đúng 0
Bình luận (0)
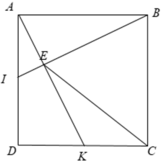
Cho hình vuông ABCD. Gọi I,K lần lượt là trung điểm của AD và DC. Chứng minh rằng BI ⊥ AK.
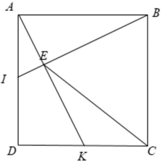
Xét Δ BAI và Δ ADK có:
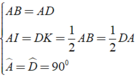
⇒ Δ BAI = Δ ADK ( c - g - c )
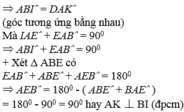
Đúng 0
Bình luận (0)
Cho hình vuông ABCD. Gọi I,K lần lượt là trung điểm của AD và DC. Chứng minh rằng BI ⊥ AK.
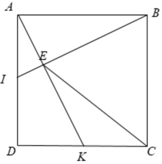
Xét Δ BAI và Δ ADK có:
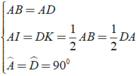
⇒ Δ BAI = Δ ADK ( c - g - c )

Đúng 0
Bình luận (0)
Cho hình vuông ABCD. Gọi I, K theo thứ tự là trung điểm của các cạnh AB, CD. Nối CI, AK. CMR: a) Tứ giác AICK là hình bình hành. b) Gọi M là trung điểm của BC. Gọi P, Q lần lượt là giao điểm của DM với IC và AK. CMR: DM = AK và DM vuông AK
a: Xét tứ giác AICK có
AI//CK
AI=CK
Do đó: AICK là hình bình hành
Đúng 0
Bình luận (0)
Cho hình thang ABCD có AB // CD, AB<CD. Gọi P,Q,T lần lượt là trung điểm của AD, AC, BC. Gọi R,K lần lượt là trung điểm của AQ và DQ. G là giao điểm của AK và DR
a) CMR: 3 điểm P, G, Q thẳng hàng
b) CM : GQ= 1/3 DC