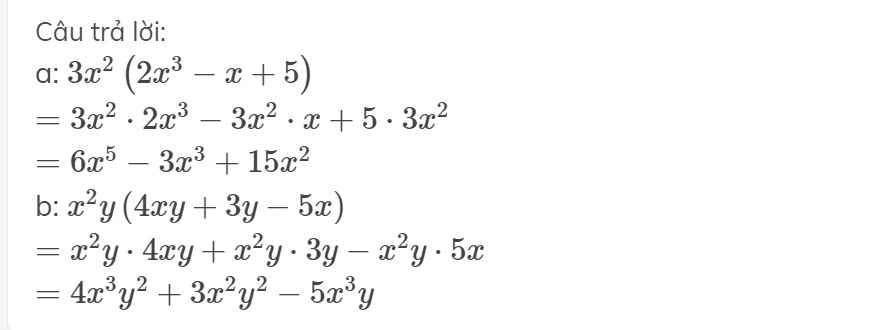a)9x^3y^2+3x^2y^2 b)x^3+2x^2+3x c)6x^2y+4xy^2+2xy d)5x^2 (x-2y)-15x (x-2y) Help me zứi

Những câu hỏi liên quan
bài 1 phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
6) 9x^3y^2+3x^2y^2
7) x^3+2x^2+3x
8) 6x^2y +4xy^2+2xy
9) 5x^2.(x-2y)-15x.(x-2y)
10) 3.(x-y)-5x.(y-x)
6) \(9x^3y^2+3x^2y^2=3x^2y^2\left(3x+1\right)\)
7) \(x^3+2x^2+3x=x\left(x^2+2x+3\right)\)
8) \(6x^2y+4xy^2+2xy=2xy\left(3x+2y+1\right)\)
9) \(5x^2\left(x-2y\right)-15x\left(x-2y\right)=5x\left(x-2y\right)\left(x-3\right)\)
10) \(3\left(x-y\right)-5x\left(y-x\right)=\left(x-y\right)\left(3+5x\right)\)
6) 9x3y2 + 3x2y2 = 3x2y2( 3x + 1 )
7) x3 + 2x2 + 3x = x( x2 + 2x + 3 )
8) 6x2y + 4xy2 + 2xy = 2xy( 3x + 2y + 1 )
9) 5x2( x - 2y ) - 15x( x - 2y ) = 5x( x - 2y )( x - 3 )
10 3( x - y ) - 5x( y - x ) = 3( x - y ) + 5x( x - y ) = ( x - y )( 3 + 5x )
a, \(9x^3y^2+3x^2y^2=3x^2y^2\left(3x+1\right)\)
b, \(x^3+2x^2+3x=x\left(x^2+2x+3\right)\)
c, \(6x^2y+4xy^2+2xy=2xy\left(3x+2y+1\right)\)
d, \(5x^2\left(x-2y\right)-15x\left(x-2y\right)=\left(5x^2-15x\right)\left(x-2y\right)=5x\left(x-3\right)\left(x-2y\right)\)
e, \(3\left(x-y\right)-5x\left(y-x\right)=3\left(x-y\right)+5x\left(x-y\right)=\left(3+5x\right)\left(x-y\right)\)
thực hiên phép tính
5x^2(3x^2-4xy+2y^2)
(6x^2y^3-9x^3y^2+15x^2y^2):3x^2y
5x+10/4x-8.4-2x/x+2
a) (x + 3y) (2x2y - 6xy2)
= (x + 3y) + 2xy (x - 3y)
= 2xy [(x + 3y) (x - 3y)]
= 2xy (x2 - 3y2)
b) (6x5y2 - 9x4y3 + 15x3y4) : 3x3y2
= (6x5y2 : 3x3y2) + (-9x4y3 : 3x3y2) + (15x3y4 : 3x3y2)
= [(6 : 3) (x5 : x3) (y2 : y2)] + [(-9 : 3) (x4 : x3) (y3 : y2)] + [(15 : 3) (x3 : x3) (y4 : y2)]
= 2x2 + (-3xy) + 5y2
= 2x2 - 3xy + 5y2
BT11: Tìm hiệu A-B biếta,-x^2y+A+2xy^2-B3x^2y-4xy^2b,5xy^2-A-6yx^2+B-7xy^2+8x^2yc,3x^2y^3-A-5x^3y^2+B8x^2y^3-4x^3yd,-6x^2y^3+A-3x^3y^2-B2x^2y^3-7x^3ye,A-dfrac{3}{8}xy^2-B+dfrac{5}{6}x^2ydfrac{3}{4}x^2y-dfrac{5}{8}xy^2f,5xy^3-A-dfrac{5}{8}yx^3+Bdfrac{21}{4}xy^3-dfrac{7}{6}x^3y
Đọc tiếp
BT11: Tìm hiệu A-B biết
\(a,-x^2y+A+2xy^2-B=3x^2y-4xy^2\)
\(b,5xy^2-A-6yx^2+B=-7xy^2+8x^2y\)
\(c,3x^2y^3-A-5x^3y^2+B=8x^2y^3-4x^3y\)
\(d,-6x^2y^3+A-3x^3y^2-B=2x^2y^3-7x^3y\)
\(e,A-\dfrac{3}{8}xy^2-B+\dfrac{5}{6}x^2y=\dfrac{3}{4}x^2y-\dfrac{5}{8}xy^2\)
\(f,5xy^3-A-\dfrac{5}{8}yx^3+B=\dfrac{21}{4}xy^3-\dfrac{7}{6}x^3y\)
a: =>A-B=3x^2y-4xy^2+x^2y-2xy^2=4x^2y-6xy^2
b: =>B-A=-7xy^2+8x^2y-5xy^2+6x^2y=-12xy^2+14x^2y
=>A-B=12xy^2-14x^2y
c: =>B-A=8x^2y^3-4x^3y-3x^2y^3+5x^3y^2=5x^2y^3+x^3y^2
=>A-B=-5x^2y^3-x^3y^2
d: =>A-B=2x^2y^3-7x^3y+6x^2y^3+3x^3y^2=8x^2y^3-7x^3y+3x^3y^2
Đúng 3
Bình luận (0)
thực hiện các phép tính sau:
a,3x^2.(2x^3-x+5)=6x^5-3x^3+15x^2
b,(4xy+3y-5x)x^2y=4x^3y^2+3x^2y^2-5x^3y
a: \(3x^2\left(2x^3-x+5\right)\)
\(=3x^2\cdot2x^3-3x^2\cdot x+5\cdot3x^2\)
\(=6x^5-3x^3+15x^2\)
b: \(x^2y\left(4xy+3y-5x\right)\)
\(=x^2y\cdot4xy+x^2y\cdot3y-x^2y\cdot5x\)
\(=4x^3y^2+3x^2y^2-5x^3y\)
Đúng 0
Bình luận (0)
thực hiện các phép tính sau:
a,3x^2.(2x^3-x+5)=6x^5-3x^3+15x^2
b,(4xy+3y-5x)x^2y=4x^3y^2+3x^2y^2-5x^3y
thực hiện các phép tính sau:
a,3x^2.(2x^3-x+5)=6x^5-3x^3+15x^2
b,(4xy+3y-5x)x^2y=4x^3y^2+3x^2y^2-5x^3y
Answer:
\(3x^2.\left(2x^3-x+5\right)\)
\(=3x^2.2x^3+3x^2.(-x)+3x^2.5\)
\(=6x^5-3x^3+15x^2\)
\((4xy+3y-5x).x^2y\)
\(=4xy.x^2y+3y.x^2y-5x.x^2y\)
\(=4x^3+3x^2y^2-5x^3y\)
Tìm bậc của các đa thức sau:
a) \(x^3y^3+6x^2y^2+12xy-8
\)
b) \(x^2y+2xy^2-3x^3y+4xy^5\)
c) \(x^6y^2+3x^6y^3-7x^5y^7+5x^4y\)
d) \(2x^3+x^4y^5+3xy^7-x^4y^5+10-xy^7\)
e) \(0,5x^2y^3+3x^2y^3z^3-a.x^2y^3-x^4-x^2y^3\) với a là hằng số
a, bậc 6
b, bậc 6
c, bậc 12
d, bậc 9
e, bậc 8
Đúng 2
Bình luận (0)
Bài 1: Thực hiện các phép tính sau:
a)-2xy^2(x^3y-2x^2y^2+5xy^3)
b)(-2x)(x^3-3x^2-x+1)
c)(-10x^3+2/5y-1/3z)(-1/2zy)
d)3x^2(2x^3-x+5)
e)(4xy+3y-5x)x^2y
f)(3x^2y-6xy+9x)(-4/3xy)
\(a,-2xy^2\left(x^3y-2x^2y^2+5xy^3\right)\\ =-2x^4y^3+4x^3y^4-10x^2y^5\\ b,\left(-2x\right)\left(x^3-3x^2-x+1\right)\\ =-2x^4+6x^3+2x^2-2x\\ c,\left(-10x^3+\dfrac{2}{5}y-\dfrac{1}{3}z\right)\left(-\dfrac{1}{2}zy\right)\\ =5x^3yz-\dfrac{1}{5}y^2z+\dfrac{1}{6}yz^2\\ d,3x^2\left(2x^3-x+5\right)=6x^5-3x^3+15x^2\\ e,\left(4xy+3y-5x\right)x^2y=4x^3y^2+3x^2y^2-5x^3y\\ f,\left(3x^2y-6xy+9x\right)\left(-\dfrac{4}{3}xy\right)\\ =-4x^3y^2+8x^2y^2-12x^2y\)
Đúng 3
Bình luận (0)
Phân tích mỗi đa thức sau thành nhân tử
a)x^3-2x^2y+xy^2+xy
b)x^3+4x^2y+4xy^2-9x
c)x^3-y^3+x-y
d)4x^2-4xy+2x-y+y^2
e)9x^2-3x+2y-4y^2
f)3x^2-6xy+3y^2-5x+5y
a) Xem lại đề
b) x³ - 4x²y + 4xy² - 9x
= x(x² - 4xy + 4y² - 9)
= x[(x² - 4xy + 4y² - 3²]
= x[(x - 2y)² - 3²]
= x(x - 2y - 3)(x - 2y + 3)
c) x³ - y³ + x - y
= (x³ - y³) + (x - y)
= (x - y)(x² + xy + y²) + (x - y)
= (x - y)(x² + xy + y² + 1)
d) 4x² - 4xy + 2x - y + y²
= (4x² - 4xy + y²) + (2x - y)
= (2x - y)² + (2x - y)
= (2x - y)(2x - y + 1)
e) 9x² - 3x + 2y - 4y²
= (9x² - 4y²) - (3x - 2y)
= (3x - 2y)(3x + 2y) - (3x - 2y)
= (3x - 2y)(3x + 2y - 1)
f) 3x² - 6xy + 3y² - 5x + 5y
= (3x² - 6xy + 3y²) - (5x - 5y)
= 3(x² - 2xy + y²) - 5(x - y)
= 3(x - y)² - 5(x - y)
= (x - y)[(3(x - y) - 5]
= (x - y)(3x - 3y - 5)
Đúng 0
Bình luận (0)