cho hình chữ nhật ABCD có AB=3AD.Gọi M,N lần lượt là trung đ của AB,C,E là đ đxứng vs N qua M, I là giao đ cuar đường thăng DM. và EB
a) c/m AEBN là hình thoi
b)AEID là hình j vì sao
c)AB=6cm.Tính diện tích đa giasc AEBCD
Cho hình chữ nhật ABCD có AB=3AD. Gọi M,N lần lượt là trung điểm của AB và CD, E là điểm đối xứng với N qua M, I là giao điểm của đường thẳng DM và EB.
a)Chứng minh tứ giác AEBN là hình thoi
b)Tứ giác AEID là hình gì? Vì sao.
c)Biết AB=6cm. Tính diện tích đa giác AEBCD
Cho hình chữ nhật ABCD có AB=3AD. Gọi M, N lần lượt là trung điểm của AB và CD, E là điểm đối xứng với N qua M, I là giao điểm của đường thẳng DM và EB.
a) C/m tứ giác AEBN là hình thoi
b) Tứ giác AEID là hình gì? Vì sao?
c) Biết AB=6cm . Tính diện tích đa giác AEBCD.
Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo. Gọi M,N lần lượt là trung điểm của AO và BO.
1/ Cho AB = 8cm ; BC = 10cm.
a/ Tính diện tính hình chữ nhật ABCD.
b/ C/m DMNC là hình thang cân.
2/ Giả sử AC = 2AD. Gọi E là giao điểm của tia CN và tia DM. C/m tứ giác ADOE là hình thoi.
1:
a: \(S_{ABCD}=AB\cdot BC=80\left(cm^2\right)\)
Cho tam giác nhọn ABC (AB<AC),đường cao Ah.Gọi M là trung điểm của AB,D là điểm đối xứng với H qua M.
a)Chứng mính tứ giác AHBD là hình chữ nhật
b)Biết AB=10cm,BH= 6cm.Tính diện tích hình chữ nhật AHBD
c)Gọi I,N lần lượt là trung điểm của BC và AC.Chứng minh IHMN là hình thang cân
nhờ mọi người giảo hộ mình câu này với ạ
a: Xét tứ giác AHBD có
M là trung điểm chung của AB và HD
góc AHB=90 độ
=>AHBD là hình chữ nhật
b: \(AH=\sqrt{10^2-6^2}=8\left(cm\right)\)
\(S_{AHBD}=6\cdot8=48\left(cm^2\right)\)
c: Xét ΔABC có AM/AB=AI/AC
nênMI//BC
Xét ΔBAC có CN/CB=CI/CA
nên NI//AB và NI/AB=CN/CB=1/2
=>NI=HM
Xét tứ giác MINH có
MI//HN
MH=IN
Do đó: MINH là hình thang cân
1,Cho tam giác ABC và AM là đường trung tuyến . Từ M vẽ các đường thẳng song song vs AC AB cắt AB AC lần lượt tại D và E
a, chứng minh ADME là hình chữ nhật
b, gọi N là điểm đối xứng vs M qua D . Cm ANBM là hình thoi
C,Tính diện tích tam giác ADME biết AB=4cm AC =6cm
2, Cho hình bình hành ABCD có BC =2AB Â =60 độ . Gọi M,N lần lượt là trung điểm của BC,AD
A, tứ giác ABMC là hình gì ? Vì sao?
B,gọi K là điểm đối xứng của A qua B . Cm tứ giác AKMN là hình thang cân
C, Cm tứ giác BKCD là hình chữ nhật
Giúp mk vs
Cho hình chữ nhật ABCD có AB=3AD . Gọi M, N lần lượt là trung điểm của AB và CD, E là điểm đối xứng với N qua M, I là giao điểm của đường thẳng DM và EB.
a) C/m tứ giác AEBN là hình thoi.
b) Tứ giác AEID là hình gì? Vì sao?
c) Biết AB=6cm. Tính diện tích đa giác AEBCD.
HELP ME!!!!
Bạn tự vẽ hình nhé. mình mới nghĩ ra câu a vs c
a) Xét tứ giác AEBN có : EM=EN ( E đối xứng N qua M )
AM=MB ( M là TĐ' của AB )
=> Tg AEBN là hình bình hành ( Tg có 2 đường chéo cắt nhau tại trung điểm của mỗi đường là hbh )
mà EN vuông góc với AB ( E đối xứng N qua M )
=> hbh AEBN là hình thoi ( hbh có 2 đường chéo vuông ^ vs nhau là hình thoi )
c) Ta có AB=3BC (gt)
=> 6=3. BC=> BC=2cm
SABCD= a.b = 6.2 = 12 (cm2)
Mặt khác: AEBN là hình thoi (cmt)
=>EM=MN=2cm
SAEB = a.h:2 = 6.2:2 = 3 (cm2 )
Vậy SAEBCD= SABCD+SAEB=12+2=14 (cm2)
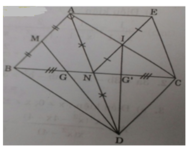
Cho tam giác ABC vuông tại A. Gọi M, N lần lượt là trung điểm của hai cạnh AB và BC.
a) Gọi D là điểm đối cứng của A qua N. Chứng minh tứ giác ABCD là hình chữ nhật.
b) Lấy I là trung điểm của cạnh AC và E là điểm đối xứng của N qua I.
Chứng minh tứ giác ANCE là hình thoi.
c) Đường thẳng BC cắt DM và DI lần lượt tại G và G’. Chứng minh BG = CG’.
d) Cho AB = 6cm, AC = 8cm. Tính diện tích ΔDGG’.
a) Ta có: NB = NC (gt); ND = NA (gt)
⇒ Tứ giác ABDC là hình bình hành
có ∠A = 90o (gt) ⇒ ABDC là hình chữ nhật.
b) Ta có: AI = IC (gt); NI = IE (gt)
⇒ AECN là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).
mặt khác ΔABC vuông có AN là trung tuyến nên AN = NC = BC/2.
Vậy tứ giác AECN là hình thoi.
c) BN và DM là 2 đường trung tuyến của tam giác ABD; BN và MD giao nhau tại G nên G là trọng tâm tam giác ABD.
Tương tự G’ là trọng tâm của hai tam giác ACD
⇒ BG = BN/3 và CG’ = CN/3 mà BN = CN (gt) ⇒ BG = CG’
d) Ta có: SABC = (1/2).AB.AC = (1/2).6.6 = 24 (cm2)
Lại có: BG = GG’ = CG’ (tính chất trọng tâm)
⇒ SDGB = SDGG' = SDG'C = 1/3 SBCD
(chung đường cao kẻ từ D và đáy bằng nhau)
Mà SBCD = SCBA (vì ΔBCD = ΔCBA (c.c.c))
⇒SDGG' = 24/3 = 8(cm2)
Cho hình chữ nhật ABCD có AB= 3AD. Gọi M ,N lần lượt là trung điểm của AB và CD, E là điểm đối xứng với N qua M. I là giao điểm của đường thẳng DM và EB.
C/m Tứ giác AEBN là hình thoi
b) Tứ giác AEID là hình gì, vì sao?
cho hcn ABCD. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA
a,CMR EFGH là hình thoi
b,Gọi M, N, P, Q lần lượt là trung điểm EF, FG, GH, HE. CMR MNPQ là hình chữ nhật
a: Xét ΔBAC có E,F lần lượt là trung điểm của BA,BC
=>EF là đường trung bình
=>EF//AC và EF=AC/2
Xét ΔDAC có
H,G lần lượt là trung điểm của DA,DC
=>HG là đường trung bình
=>HG//AC và HG=AC/2
=>EF//HG và EF=HG
Xét ΔABD có
E,H lần lượt là trung điểm của AB,AD
=>EH là đường trung bình
=>EH=BD/2
=>EH=AC/2=EF
Xét tứ giác EHGF có
EF//GH
EF=GH
EH=EF
Do đó: EHGF là hình thoi
b: Xét ΔEHF có Q,M lần lượt là trung điểm của EH,EF
=>QM là đường trung bình
=>QM//HF và QM=HF/2
Xét ΔGHF có
P,N lần lượt là trung điểm của GH,GF
=>PN là đường trung bình
=>PN//HF và PN=HF/2
=>QM//PN và QM=PN
Xét ΔHEG có HQ/HE=HP/HQ=1/2
nên PQ//EG
=>PQ vuông góc HF
=>PQ vuông góc QM
Xét tứ giác MNPQ có
MQ//NP
MQ=NP
góc PQM=90 độ
Do đó: MNPQ là hình chữ nhật