Câu 1:

Ta có: \(y=x^4-2x^2+2\Rightarrow y'=4x^3-4x=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)

Do đó 3 điểm cực trị của đồ thị hàm số là:

\(A(0;2);B(1;1);C(-1;1)\)

\(\Rightarrow \left\{\begin{matrix} AB=\sqrt{(0-1)^2+(2-1)^2}=\sqrt{2}\\ BC=\sqrt{(1--1)^2+(1-1)^2}=2\\ AC=\sqrt{(0--1)^2+(2-1)^2}=\sqrt{2}\end{matrix}\right.\)

Vì \(AB^2+AC^2=BC^2\) nên tam giác $ABC$ là tam giác vuông tại $A$

\(\Rightarrow S_{ABC}=\frac{AB.AC}{2}=\frac{\sqrt{2}.\sqrt{2}}{2}=1\)

Đáp án A

Câu 2:

Để hàm số đạt cực trị tại $x=1$ thì:

\(y'=-3(m^2+5m)x^2+12mx+6=0\) tại $x=1$

hay \(-3(m^2+5m)+12m+6=0\)

\(\Leftrightarrow m^2+m-2=0\)

\(\Leftrightarrow m=1; m=-2\)

Với m=1:

Hàm số trở thành:

\(y=-6x^3+6x^2+6x-6\)

\(y'=-18x^2+12x+6=0\Leftrightarrow x=1; x=-\frac{1}{3}\)

Lập bảng biến thiên ta thấy thỏa mãn

Với m=-2

Hàm trở thành: \(y=6x^3-12x^2+6x-6\)

\(y'=18x^2-24x+6=0\Leftrightarrow x=1; x=\frac{1}{3}\)

Lập bảng biến thiên ta thấy tại $x=1$ đạt cực tiểu nên không thỏa mãn

Vậy m=1

Đáp án A

Đáp án A

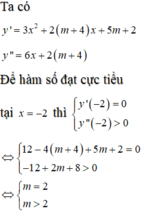
Vậy không có giá trị m thỏa mãn yêu cầu bài toán.

Lời giải:

Viết lại hàm số: \(y=\frac{1}{3}mx^3-(m-1)x^2+3(m-2)x+\frac{1}{3}\)

Ta có \(y'=mx^2-2(m-1)x+3(m-2)\)

a) Trước tiên, để hàm số đạt cực trị tại $x=0$ thì $x=0$ phải là nghiệm của pt \(y'=0\Leftrightarrow 3(m-2)=0\Leftrightarrow m=2\)

Thử lại: \(y'=2x^2-2x\)

\(y'=0\Leftrightarrow x=0\) hoặc \(x=1\). Lập bảng biến thiên ta thấy đúng là $y$ cực đại tại $x=0$

Vậy $m=2$

b) Tương tự như phần a, để hàm số đạt cực trị tại $x=-1$ thì $x=-1$ phải là nghiệm của pt \(y'=0\)

\(\Leftrightarrow m(-1)^2-2(m-1)(-1)+3(m-2)=0\)

\(\Leftrightarrow m=\frac{4}{3}\)

Thử lại: \(y'=\frac{4}{3}x^2-\frac{2}{3}x-2\). Có \(y'=0\Leftrightarrow x=\frac{3}{2}\) hoặc $x=-1$. Lập bảng biến thiên ta thấy $y$ cực tiểu tại $x=\frac{3}{2}$ chứ không phải tại $x=-1$

Vậy không tồn tại $m$ thỏa mãn.

c) Hàm số có cực đại và cực tiểu khi $y'=0$ có hai nghiệm phân biệt.

Hay $mx^2-2(m-1)x+3(m-2)=0$ có hai nghiệm phân biệt

Do đó \(\left\{\begin{matrix} m\neq 0\\ \Delta'=(m-1)^2-3m(m-2)>0\end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix} m\neq 0\\ -2m^2+4m+1>0\Leftrightarrow \frac{2-\sqrt{6}}{2}< m< \frac{2+\sqrt{6}}{2}\end{matrix}\right.\)

d) Điểm cực trị của hàm số chính là nghiệm của $y'=0$

Với ĐKXĐ như phần c, áp dụng hệ thức Viete:

\(\left\{\begin{matrix} x_1+x_2=\frac{2(m-1)}{m}\\ x_1x_2=\frac{3(m-2)}{m}\end{matrix}\right.\)

Nếu \(x_1+2x_2=1\Rightarrow x_2=1-(x_1+x_2)=\frac{2-m}{m}\)

Mà \(x_1x_2=\frac{3(m-2)}{m}\Rightarrow x_1=-3\)

Khi đó: \(1=x_1+2x_2=-3+\frac{2-m}{m}=-4+\frac{2}{m}\Rightarrow m=\frac{2}{5}\)

Thử lại thấy thỏa mãn đkxđ. Vậy $m=\frac{2}{5}$

\(y'=6x^2-6\left(m+1\right)x+6m\)

ta có y/y'=\(\left(3m-1\right)x+m^3+m^2+m\)

suy ra y= \(\left(3m-1\right)x+m^3+m^2+m\)là pt của dường thẳng đi qua A và B

de-ta \(=9\left(m+1\right)^2-36m\)

y' có 2 \(n_o\)phân biệt khi m#1

hai hoành độ của hai điểm cực trị là :

\(X=\dfrac{-b\left(+,-\right)\sqrt{deta}}{a}=\)

\(\left[{}\begin{matrix}\dfrac{m+3}{2}\\\dfrac{3m-1}{2}\end{matrix}\right.\)<=>y=\(\left[{}\begin{matrix}2m^3+5m^2+10m+3\\2m^3+11m^2+4m+1\end{matrix}\right.\)(tìm y bằng cách thế x vào pt đường thẳng )

khoảng cách giữa hai điểm AB =\(\sqrt{2}\)

ta có pt : \(2=\left(\dfrac{m+3}{2}-\dfrac{3m-1}{2}\right)^2+\left(2m^3+5m^2+10m-3-\left(2m^3+11m^2-4m+1\right)\right)^2\)

lại sai chỗ nào rồi 0 ra nghiệm , cậu tính lại thử , cách giả là như vậy

\(y'=4x^3-4\left(m^2-m+1\right)x\)

\(=4x\left(x^2-\left(m^2-m+1\right)\right)\)

có 1 n0 x=0

2 nghiệm còn lại là : \(\left(+,-\right)\sqrt{m^2-m+1}\) (thỏa với mọi m)

ta thấy 0 ở giữa hai nghiệm và hệ số a cùa y' =4(+)

theo bảng biến thiên ta thấy (cái bảng vẽ mệt quá) : \(-\sqrt{m^2-m+1}và+\sqrt{m^2-m+1}\)

là hai điểm cực tiểu , và ta thấy nó dối xứng với nhau qua trục tung nên khoảng cách giữa hai điểm cực tiểu ngắn nhất khi \(\sqrt{m^2-m+1}\)nhỏ nhất khi m=0

vậy để có 1 điểm cực đại và hai điểm cực tiểu thì m thỏa mãng với mọi , và để có khoảng cách giữa hai điểm cực tiểu ngắn nhất khi m = 0

vậy m =0 thỏa yêu cầu

câu 3 cụng vậy m thỏa với mọi để có 3 điểm A,B,C và B, C có hoàng độ là \(\left(+,-\right)\sqrt{4m}\) dối xứng qua trục tung

=> khoảng cách là : \(\sqrt{4m}\) nhỏ nhất m=0

Ta biết hàm số y = f(x) có cực trị khi phương trình y’ = 0 có nghiệm và y’ đổi dấu khi qua các nghiệm đó.

Ta có:

Xét y’ = 0, ta có: y′ = 3 x 2  − 2mx + (m – 2/3)

∆ ’ > 0 khi m < 1 hoặc m > 2 (∗)

Để hàm số có cực trị tại x = 1 thì

y′(1) = 3 − 2m + m – 2/3 = 0 ⇔ m = 7/3, thỏa mãn điều kiện (∗)

Với m = 7/3 thì hàm số đã cho trở thành:

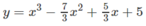
Ta có:

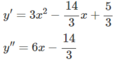
Vì y′′(1) = 6 – (14/3) > 0 nên hàm số đạt cực tiểu tại x = 1 và y CT  = y(1) = (16/3).

Ta biết hàm số y = f(x) có cực trị khi phương trình y’ = 0 có nghiệm và y’ đổi dấu khi qua các nghiệm đó.

Ta có:

Xét y’ = 0, ta có: y′ = 3 x 2  − 2mx + (m – 2/3)

Δ’ > 0 khi m < 1 hoặc m > 2 (∗)

Để hàm số có cực trị tại x = 1 thì

y′(1) = 3 − 2m + m – 2/3 = 0 ⇔ m = 7/3, thỏa mãn điều kiện (∗)

Với m = 7/3 thì hàm số đã cho trở thành:

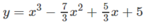
Ta có:

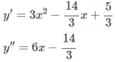
Vì y′′(1) = 6 – (14/3) > 0 nên hàm số đạt cực tiểu tại x = 1 và y C T  = y(1) = (16/3).