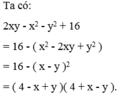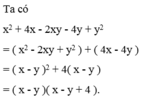phân tích thành nhân tử giúp mình x2 - 2xy + y2 -n2 + 2mn - m2

Những câu hỏi liên quan
Phân tích các đa thức sau thành nhân tử:a) 5
x
3
- 3
x
2
y - 45x
y
2
+ 27
y
3
;b) 3
x
2
(a - b + c) + 36xy(a - b + c) + 108
y
2
(a - b + c);c)
x
2
-2xy +
y...
Đọc tiếp
Phân tích các đa thức sau thành nhân tử:
a) 5 x 3 - 3 x 2 y - 45x y 2 + 27 y 3 ;
b) 3 x 2 (a - b + c) + 36xy(a - b + c) + 108 y 2 (a - b + c);
c) x 2 -2xy + y 2 - 4 m 2 + 4mn - n 2
a) (5x - 3y)(x - 3y)(x + 3y).
b) 3(a – b + c) ( x + 6 y ) 2 .
c) (x-y-2m + n)(x-y + 2m-n)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử
3x2(a-b+c)+36xy(a-b+c)+108y2(a-b+c)
x2-2xy+y2-4m2+4mn-n2
\(3x^2\left(a-b+c\right)+36xy\left(a-b+c\right)+108y^2\left(a-b+c\right)\)
\(=\left(a-b+c\right)\left(3x^2+36xy+108y^2\right)\)
\(=3\left(a-b+c\right)\left(x^2+12xy+36y^2\right)\)
\(=3\left(a-b+c\right)\left(x+6y\right)^2\)
___________________
\(x^2-2xy+y^2-4m^2+4mn-n^2\)
\(=\left(x^2-2xy+y^2\right)-\left(4m^2-4mn+n^2\right)\)
\(=\left(x-y\right)^2-\left(2m-n\right)^2\)
\(=\left(x-y-2m+n\right)\left(x-y+2m-n\right)\)
Đúng 3
Bình luận (0)
Câu 1:Phân tích đa thức thành nhân tửa/ –6x2y + xy2b/10a2c – 90b2c + 30bc2 – 10ac2 c/ax + bc – ac – bxd/36 – x2 + 4xy – 4y2 e/ m2 + n2 + 4m + 4n + 2mn f/ 2x2 – 1/2y2
Đọc tiếp
Câu 1:Phân tích đa thức thành nhân tử
a/ –6x2y + xy2
b/10a2c – 90b2c + 30bc2 – 10ac2
c/ax + bc – ac – bx
d/36 – x2 + 4xy – 4y2
e/ m2 + n2 + 4m + 4n + 2mn
f/ 2x2 – 1/2y2
\(a,=xy\left(-6x+y\right)\)
\(b,=10c\left(a^2-9b^2+3bc-ac\right)=10c\left[\left(a-3b\right)\left(a+3b\right)-c\left(a-3b\right)\right]\)
\(=10c\left[\left(a-3b\right)\left(a+3b-c\right)\right]\)
c,\(=a\left(x-c\right)-b\left(x-c\right)=\left(a-b\right)\left(x-c\right)\)
d,\(=-\left(x-2y-6\right)\left(x-2y+6\right)\)
e;\(=m^2+4m+mn+n^2+4n+mn=m\left(m+4+n\right)+n\left(m+4+n\right)\)\(=\left(m+n\right)\left(m+n+4\right)\)
f,\(=\dfrac{1}{2}\left(4x^2-y^2\right)=\dfrac{1}{2}\left(2x-y\right)\left(2x+y\right)\)
Đúng 1
Bình luận (0)
Phân tích thành nhân tử: x 2 – 2xy + y 2 - z 2
x 2 – 2xy + y 2 - z 2
= ( x 2 – 2xy + y 2 ) – z 2
= x - y 2 – z 2
= (x – y + z)(x – y – z)
Đúng 0
Bình luận (0)
Khi phân tích đa thức x2 + 4x – 2xy – 4y + y2 thành nhân tử, bạn Việt làm như sau: x2 + 4x – 2xy – 4y + y2 (x2 - 2xy + y2) + (4x – 4y) (x - y)2 + 4(x – y) (x – y)(x – y + 4). Em hãy chỉ rõ trong cách làm trên, bạn Việt đã sử dụng những phương pháp nào để phân tích đa thức thành nhân tử.
Đọc tiếp
Khi phân tích đa thức x2 + 4x – 2xy – 4y + y2 thành nhân tử, bạn Việt làm như sau:
x2 + 4x – 2xy – 4y + y2 = (x2 - 2xy + y2) + (4x – 4y)
= (x - y)2 + 4(x – y)
= (x – y)(x – y + 4).
Em hãy chỉ rõ trong cách làm trên, bạn Việt đã sử dụng những phương pháp nào để phân tích đa thức thành nhân tử.
x2 + 4x – 2xy – 4y + y2 = (x2-2xy+ y2) + (4x – 4y) → bạn Việt dùng phương pháp nhóm hạng tử
= (x - y)2 + 4(x – y) → bạn Việt dùng phương pháp dùng hằng đẳng thức và đặt nhân tử chung
= (x – y)(x – y + 4) → bạn Việt dùng phương pháp đặt nhân tử chung
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử
[ (x2 + y2)(z2 + t2) + 4xyzt ]2 - [ 2xy(z2 + t2) + 2zt(x2 + y2) ]
Phân tích đa thức thành nhân tử 2 x y - x 2 - y 2 + 16
phân tích các đa thức sau thành nhân tử
a x2 - y2 -3x + 3y
b 2x + 2y -x2 + y2
c x2 -16 + y2 + 2xy
cứuuu
a) \(x^2-y^2-3x+3y\)
\(=\left(x-y\right)\left(x+y\right)-3\left(x-y\right)\)
\(=\left(x-y\right)\left(x+y-3\right)\)
b) \(2x+2y-x^2+y^2\)
\(=2\left(x+y\right)-\left(x^2-y^2\right)\)
\(=2\left(x+y\right)-\left(x-y\right)\left(x+y\right)\)
\(=\left(x+y\right)\left(2-x+y\right)\)
c) \(x^2-16+y^2+2xy\)
\(=x^2+y^2+2xy-16\)
\(=\left(x+y\right)^2-16\)
\(=\left(x+y+4\right)\left(x+y-4\right)\)
Đúng 1
Bình luận (0)
a) \(x^2-y^2-3x+3y\)
\(=\left(ax+y\right)\left(ax-y\right)-3.\left(x-y\right)\)
b) \(2x+2y-x^2+y^2\)
\(=2\left(x+y\right)-\left(x+y\right)\left(x-y\right)\)
c) \(x^2-16+y^2+2xy\)
\(=\left(x+y\right)\left(x-y\right)+2xy-16\)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử x 2 + 4 x - 2 x y - 4 y + y 2
x^2+4x-2xy-4y+y^2=(x^2-2xy+y^2)+(4x-4y)
=(x-y)^2+4(x-y)
=(x-y)(x-y+4)
Đúng 0
Bình luận (0)
Phân tích đa thức sau thành nhân tử: 2xy – x2 – y2 + 16
2xy – x2 – y2 + 16 (Có 2xy ; x2 ; y2, ta liên tưởng đến HĐT (1) hoặc (2))
= 16 – (x2 – 2xy + y2)
= 42 – (x – y)2 (xuất hiện hằng đẳng thức (3))
= [4 – (x – y)][4 + (x - y)]
= (4 – x + y)(4 + x – y).
Đúng 0
Bình luận (0)