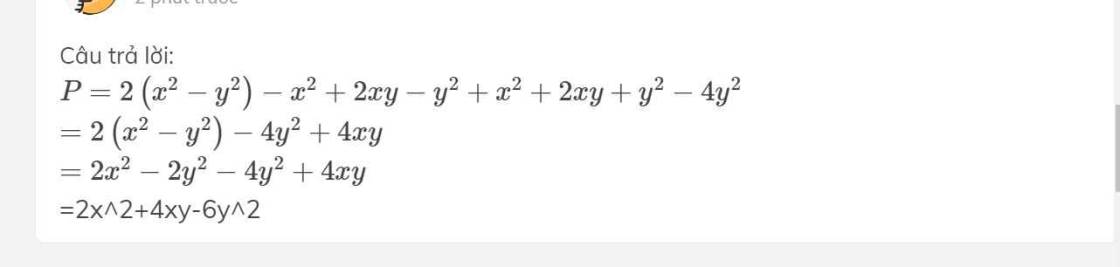rut gon bieu thuc sau : P=2(x+y)(x-y)-(x-y)^2+(x+y)^2-4y^2

Những câu hỏi liên quan
rut gon bieu thuc sau P=\(2\left(x+y\right)\left(x-y\right)-\left(x-y\right)^2+\left(x+y\right)^2-4y^2\)
Rut gon cac bieu thuc sau:
a,(x-2y)^2+(x+2y)^2
b,2(x-y).(x+y) +(x+y)^2+(x-y)^2
a) \(\left(x-2y\right)^2+\left(x+2y\right)^2=x^2-4xy+4y^2+x^2+4xy+4y^2=2x^2+8y^2\)
b) \(2\left(x-y\right)\left(x+y\right)+\left(x+y\right)^2+\left(x-y\right)^2=2\left(x^2-y^2\right)+x^2+2xy+y^2+x^2-2xy^2+y^2\)
\(=2x^2-2y^2+2x^2+2y^2=4x^2\)
Đúng 0
Bình luận (0)
\(a,\left(x-2y\right)^2+\left(x+2y\right)^2\)
\(=\left(x^2-4xy+4y^2\right)
+\left(x^2+4xy+4y^2\right)\)
\(=2x^2+8y^2\)
\(b,2\left(x-y\right).\left(x+y\right)+\left(x+y\right)^2+\left(x-y\right)^2\)
\(=2\left(x^2-y^2\right)+\left(x^2+2xy+y^2\right)+\left(x^2-2xy+y^2\right)\)
\(=2x^2-2y^2+2x^2+2y^2\)
\(=4x^2\)
Đúng 0
Bình luận (0)
a)\(\left(x-2y\right)^2+\left(x+2y\right)^2\)
\(=x^2-4xy+4y^2+x^2+4xy+y^2\)
\(=2\left(x^2+y^2\right)\)
b)\(2\left(x-y\right)\left(x+y\right)+\left(x+y\right)^2+\left(x-y\right)^2\)
\(=\left(x+y\right)^2+2\left(x+y\right)\left(x-y\right)+\left(x-y\right)^2\)
\(=\left(x+y-x+y\right)^2=y^2\)
Đúng 0
Bình luận (0)
rut gon bieu thuc [(x^3+y^3)-2(x^2-y^2)+3(x+y)^2]:(x+y)
Rut gon cac bieu thuc sau
A) 2x^2(1-3x)+6x^3
B) (x-y)^2+(x+y)^2+2(x-y)(x+y)
A) 2x2(1-3x)+6x3
=2x2*(1-3x)+2x2*3x
=2x2*(1-3x+3x)
=2x2
B) (x-y)2+(x+y)2+2(x-y)(x+y)
=2(x2-y2)+x2+2xy+y2+x2-2xy+y2
=2x2-2y2+x2+2xy+y2+x2-2xy+y2
=4x2
Đúng 0
Bình luận (0)
B1: rut gon bieu thuc
a, (x+y)^2-4(x-y)^2
b, 2(x-y)(x+y)+(x+y)^2+(x-y)^2
B2: tim X
a, (2X-1)^2-4(X+2)^2=9
b, 3(X-1)^2-3X(X-5)=21
B3: Cho bieu thuc
M=(x+3)^3-(x-1)^3+12x(x-1)
a, Rut gon bieu thuc tren
b, Tinh gia tri M tai x=-2/3
c, Tim x de M=16
1)a)=>x2+y2+2xy-4(x2-y2-2xy)
=>x2+y2+2xy-4.x2+4y2+8xy
=>-3.x2+5y2+10xy
Đúng 0
Bình luận (0)
Thuc hien phep nhan rut gon roi tinh gia tri bieu thuc
B)x(x^2-y)-x^2(x+y)+y(x^2-x) tai x=1/2 va y=-100
=x^3-xy-x^3-x^2y+x^2y--xy
=-2xy
thay x=1\2 va y bang 100 vao Bta duoc
B= -2.1\2.100=-100
Đúng 0
Bình luận (0)
rut gon bieu thuc
p=(x^2+2xy)^2+2(x^2+2xy)y^2+y^4
\(P=\left(x^2+2xy\right)^2+2\left(x^2+2xy\right)y^2+y^4\)
\(=x^4+4x^3y+4x^2y^2+2x^2y^2+4xy^3+y^4\)
\(=x^4+y^4+6x^2y^2+4x^3y+4xy^3\)
P = ( x2 + 2xy )2 + 2( x2 + 2xy )y2 + y4
= ( x2 + 2xy )2 + 2( x2 + 2xy )y2 + ( y2 )2
= ( x2 + 2xy + y2 )2
= [ ( x + y )2 ]2
= ( x + y )4
Bài làm :
Ta có :
P = ( x2 + 2xy )2 + 2( x2 + 2xy )y2 + y4
P = ( x2 + 2xy )2 + 2( x2 + 2xy )y2 + ( y2 )2
P = ( x2 + 2xy + y2 )2
P = [ ( x + y )2 ]2
P = ( x + y )4
Vậy P = (x + y)4
Xem thêm câu trả lời
Rut gon cac bieu thuc sau:
2(x-y).(x+y)+(x-y)^2+(x+y)^2
(2x-3).(4x^2+6x+9) -(54+8x)
(3x+y).(9x^2-3xy+y^2)-(3x-y).(9x^2+3xy+y^2)
(a +b +c)^2-(a-c)^2-2ab+2bc
\(a,\)\(2\left(x-y\right)\left(x+y\right)+\left(x-y\right)^2+\left(x+y\right)^2.\)
\(=\left[\left(x-y\right)+\left(x+y\right)\right]^2=\left(x-y+x+y\right)^2=x^2\)
\(b,\)\(\left(2x-3\right)\left(4x^2+6x+9\right)-\left(54+8x\right)\)
\(=8x^2-27-54-8x=8x^2-8x-81\)
\(c,\)\(\left(3x+y\right)\left(9x^2-3xy+y^2\right)-\left(3x-y\right)\left(9x^2+3xy+y^2\right)\)
\(=27x^3+y^3-\left(27x^3-y^3\right)=2y^3\)
\(d,\)\(\left(a+b+c\right)^2-\left(a-c\right)^2-2ab+2bc\)
\(=a^2+b^2+c^2+2ab+2bc+2ac-a^2+2ac-c^2-2ab+2bc\)
\(=b^2+4bc+4ac\)
Đúng 0
Bình luận (0)
rut gon bieu thuc
a/ (x+y)(x2-xy+y2)-(x-y)(x2+xy+y2)
b/ (x-y)2+ (x+y)2
a) ( x + y)( x^2 - xy+ y^2 )- ( x - y)( x^2 + xy + y^2 )
= x^3 +y^3 - ( x^3 - y^3 )
= x^3 + y^3 - x^3 + y^3
= 2y^3
b; ( x - y)^2 + ( x + y)^2
= x^2 - 2xy + y^2 + x^2 + 2xy + y^2
= 2x^2 + 2y^2
Đúng 0
Bình luận (0)